Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Սկիզբը
Նախորդ հատվածը

Գլուխ 7
Խորանում ենք մինչև արմատները

Բարձր աստիճաններից իջնում ենք ցածրերին

Մեզ համար արդեն պարզել ենք, որ յուրաքանչյուր մաթեմատիկական գործողության համապատասխանում է համանման, սակայն հակառակ ուղղության գործողություն:

Գումարման համար այդպիսի հակառակ գործողությունը հանումն է, բազմապատկման համար՝ բաժանումը: Այժմ փորձենք պարզել, թե աստիճան բարձրացնելու հակառակ գործողությունը որն է: Քանի որ աստիճան բարձրացնելը բազմակի բազմապատկումն է, ակնհայտ է, որ հակառակ գործողությունը բազմակի բաժանումը կլինի:

Օրինակ՝ 32-ը կարելի է բաժանել 2-ի և 16 ստանալ, հետո 16-ը բաժանել 2-ի և 8 ստանալ, հետո 8-ը բաժանել 2-ի՝ 4 ստանալ, հետո 4-ը՝ 2-ի և 2 ստանալ, հետո 2-ը՝ 2-ի և 1 ստանալ: Այս գործողությունները կարճ կարելի է գրել այսպես՝ 32:2:2:2:2:2 = 1. (Ինչպես բաժանման դեպքում, որը ուսումնասիրեցինք երրորդ գլխում, մեր խնդիրը 1-ին հասնելն է)։ Քանի որ 5 անգամ բաժանում ենք կատարել և հասել ենք 1-ի, կարելի է ասել, որ 2-ը հինգ աստիճանի արմատ է 32-ից:

Եթե դիտարկենք 81 թիվը, կտեսնենք, որ 81:3:3:3:3=1, այսպիսով 3-ը չորրորդ աստիճանի արմատ է 81-ից: (Ինչո՞ւ հենց արմատ: Որտեղի՞ց հայտնվեց այս բառը: Կարելի է բացատրել հետևյալ կերպ՝ 32 թիվն աճում է 2 հիմքից, իսկ 81-ը՝ 3 հիմքից այնպես, ինչպես բույսերը՝ արմատներից)։

Այսպիսի մաթեմատիակական գործողություն նշանակվում է 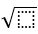 : Արմատների բազմազանությունը ցույց է տալիս արմատի վերևի ձախ մասի թիվը: Այսպես, հինգերորդ աստիճանի արմատ 32-ից կարելի է գրել  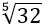, չորրորդ աստիճանի արմատ 81-ից կարելի է գրել  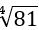: նշանը անվանում են ռադիկալի նշան, իսկ արմատ պարունակող թվերը՝ ռադիկալներ: «Ռադիկալ» բառը մեզ է հասել լատիներենից, որը «արմատ» է նշանակում:

Հազվադեպ ենք բարձր աստիճանների հանդիպում, հաճախ գործ ենք ունենում երկրորդ, այսինքն՝ քառակուսի աստիճանի բարձրացնելու հակադարձ գործողությունների հետ: Երկրորդ աստիճանի արմատի հանելը կոչվում է քառակուսի արմատ հանել, իսկ 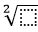 նշանը կոչվում է քառակուսի արմատ, ընդ որում ձախ կողմի երկուսը հաճախ չի գրվում: Հետագայում  նշանը՝ առանց ձախ կողմի վերև թվի, միշտ նկատի կունենանք քառակուսի արմատ:

Ի՞նչ է թվի քառակուսի արմատը: 25-ը 5-ի քառակուսին է, այսպիսով կարելի է ասել, որ 5-ը քառակուսի արմատ է 25-ից, կամ 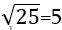: Այդ պատճառով պետք է ասել «հինգը երկրորդ աստիճանի արմատ է 25-ից», բայց սովորաբար գործածում են «քառակուսի արմատ» անվանումը: (Նույն ձևով երրորդ աստիճանի արմատն անվանում են խորանարդ արմատ):

Հաջորդ խնդիրը որոշակի թվից ինչ-որ աստիճանի արմատը գտնելն է: Այստեղ կարելի է հակառակից եկող ճանապարհով գնալ: Ենթադրենք, գիտենք, որ 2⁵=32, նշանակում է, եթե 32-ը հինգ անգամ բաժանենք 2-ի, ապա արդյունքը 1 կլինի: (Եթե թիվն ինչ-որ աստիճան ենք բարձրացրել, դժվար չէ հակառակ կարգով գնալը)։

Գործնականում արմատի որոշման թվաբանական մեթոդը հակառակ գործողությունների շարք է: Փորձենք 625-ից քառակուսի արմատ հանել: Արմատ հանելու սխեման հետևյալն է. 

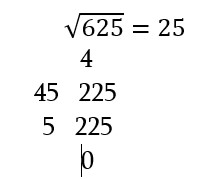
Պատասխանի առաջին թիվը՝ 2, ստանում ենք ընտրելով: Գիտենք, որ 2x2=4, դա 6-ից փոքր հնարավոր մոտակա թիվն է, քանի որ 3x3=9, որն էլ 6-ից մեծ է: Հետո հանում ենք կատարում և մեկի փոխարեն երկու թվանշան ենք իջեցնում, ինչը ընդունված է սովորական սյունակով բաժանման ժամանակ: (Եթե խորանադ արմատ հանելու լինեինք, երեք թվանշան կիջեցնեինք, իսկ չորրորդ աստիճանի արմատի դեպքում՝ չորս թվանշան, և այդպես շարունակ)։ Հաջորդ թվանշանն ստանալու համար պետք է 225-ը 45-ի բաժանել: 45 թիվը կստանաք՝ կրկնապատկելով պատասխանի առաջին թիվը, որը կլինի 4: Երկրորդ թվանշանը պետք է հավասար լինի պատասխանի երկրորդ թվանշանին, այդպիսով, այն նույնպես կարելի է ընտրելով գտնել, այնպես, որպեսզի 225-ի մոտ թիվ ստանանք: 5 թվանշանն ամենահարմարն է, քանի որ 5х45=225:

Այդ գործընթացը կարող է շատ դժվար թվալ, և դուք լիովին ճիշտ կլինեք: Թվաբանական եղանակով թվերի արմատները որոշելը շատ դժվար է, սակայն արդյունքները տարբեր հաշվարկների ժամանակ օգտակար են:

Դիտարկենք հաջորդ օրինակը: Ինչի՞ է հավասար -ը: Ի՞նչ թիվ պետք է քառակուսի բարձրացնենք, որպեսզի 2 ստանանք:

Կարող ենք միանգամից որոշել, որ ամբողջ թվերի մեջ այդպիսի թիվ չկա, քանի որ 1x1=1, իսկ 2х2=4: Առաջին թիվը շատ փոքր է, իսկ երկրորդը՝ շատ մեծ: Հետևաբար, պատասխանը կոտորակային թիվ կլինի:

Ընդհանրապես, հնարավո՞ր է, որ գոյություն ունենա քառակուսի արմատ կոտորակային թվի տեսքով: Իսկ ինչո՞ւ ոչ: Համաձայն աստիճանային արտահայտությունների մեր սահմանման 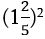–ը 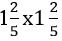–ն է, որի պատասխանը  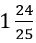թիվն է:

Իսկ դա իր հերթին նշանակում է, որ 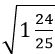 հավասար է 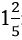: Այժմ համոզվեցինք, որ ոչ միայն քառակուսի արմատը կարող է կոտորակային թիվ լինել, այլև՝ թվի քառակուսին: Երկու դեպքում էլ ճշմարիտ են նույն կանոնները, ինչ որ ամբողջ թվերի դեպքում:
Դրանից բացի, պատահաբար ստացվեց, որ 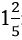թիվը ինքն իրենով բազմապատկելիս արդյունքում 2-ին մոտ թիվ է ստացվում: Այստեղից հետևում է, որ  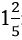թիվը մոտ է –ին: Միայն 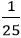 է բաժանում փնտրվող պատասխանից, քանի որ (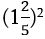-ը 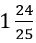 է, իսկ մեզ անհրաժեշտ է 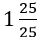, այսինքն՝ 2 ստանալ: Սակայն կարելի է և ավելի ճշգրիտ պատասխան ստանալ: Եթե 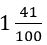կոտորակային թիվը բազմապատկենք իրենով, կստանանք  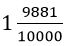, որը շատ ավելի մոտ է 2-ին: Կարող է թվալ, որ եթե ավելի ճշգրիտ հաշվարկներ կատարենք, վաղ թե ուշ կգտնենք կոտորակային թվի ճշգրիտ արժեքը, որը հանդիսանում է 2-ի քառակուսի արմատը, չնայած, հնարավոր է, դա շատ բարդ թիվ լինի:

Բայց այդպե՞ս է, ահա, թե որն է հարցը:

Համեմատում ենք գծերը

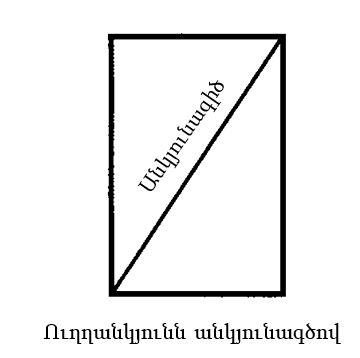
Առաջին անգամ 2–ի քառակուսի արմատի որոնմամբ զբաղվել են դեռևս Հին Հունաստանի մաթեմատիկոսները: Ինչպես արդեն ասել եմ, նրանք առաջին հերթին երկրաչափներ էին ու նրանց հետաքրքրում էին երկրաչափական պատկերների հատվածների երկարությունների հարաբերությունները: Օրինակ, եթե ուղղանկյան անկյունագիծը տանենք, ինչպես նկարում է ցույց տրված, ինչպիսի՞ հարաբերության մեջ կլինեն անկյունագծի և ուղղանկյան կողմերի երկարությունները: Ակնհայտ է, որ անկյունագիծը երկար է, բայց ինչքա՞ն: Հին հույներն ուզում էին այս հարցի պատասխանը գտնել:

Ենթադրենք, երկու հատված ենք համեմատում: Թող նրանցից մեկի երկարությունը 2 սմ լինի, իսկ մյուսինը՝ 1 սմ: Հետևաբար, կարող ենք ասել, որ հատվածների երկարությունները հարաբերում են ինչպես 2-ը 1-ի, կամ հատվածներից մեկ երկու անգամ երկար է մյուսից: Եթե մի հատվածի երկարությունը 4 սմ է, իսկ մյուսինը՝ 2սմ, կարող ենք ասել, որ հատվածների երկարությունները հարաբերում են ինչպես 4-ը 2-ի:

Երկու դեպքում էլ հատվածներից մեկի երկարությունը երկու անգամ մեծ է մյուսի երկարությունից: Մաթեմատիկոսի տեսանկյունից, մեծությունների հարաբերությունն ավելի մեծ հետաքրքրություն է իրենից ներկայացնում, քան նրանց բացարձակ արժեքները: Այնքան էլ կարևոր չէ, որ մի դեպքում երկարությունները հավասար են 4 և 2 սմ, իսկ մյուսում՝ 48 և 24 սմ: Մաթեմատիկոսը երկու դեպքում էլ ուշադրություն կդարձնի, որ հատվածներից մեկի երկարությունը երկու անգամ մեծ է մյուսից, այսինքն՝ նրանք հարաբերում են ինչպես 2-ը 1-ի:

Մեծությունների հարաբերությունը ներկայացնելու ամենահարմար ձևը կոտորակն է: Եթե մի հատվածի երկարությունը հավասար է 2 սմ, իսկ մյուսինը՝ 1 սմ, նշանակում է նրանց հարաբերությունը հավասար է 2/1:

Եթե մի հատվածի երկարությունը հավասար է 48 սմ, իսկ մյուսինը՝ 24 սմ, ապա նրանց հարաբերությունը հավասար է 48/24, կամ էլ 2/1, եթե կրճատենք 24-ով:

Երկու նմանատիպ մեծությունների հարաբերությունն արտահայտող կոտորակը անվանում ենք հարաբերակցություն: (Այդպիսի մեծություններ կարող են լինել և՛ հատվածների երկարությունները, և՛ անոթների ծավալները, և՛ երկու մարդկանց քաշերը, և այլն)։

Իհարկե, հարաբերությունը կարող է այդպես պարզ չլինել, ինչպես՝ 2:1. Ենթադրենք, մի հատվածի երկարությունը մեկ սանտիմետր է, իսկ մյուսինը՝  : Այդ դեպքում հարաբերությունը կլինի 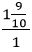 ։ Այս արտահայտությունը կարելի է պարզեցնել վերին և ստորին մասերը 10-ով բազմապատկելով: Կստանանք, որ հարաբերությունը հավասար է :

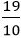Կոտորակային տեսքով արտահայտված ցանկացած երկու թվերի հարաբերություններ կարելի է ներկայացնել երկու ամբողջ թվերի հարաբերության տեսքով: Օրինակ, ունենք երկու հատված մեկի երկարությունը 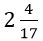 սանտիմետր է, իսկ մյուսինը՝  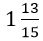սանտիմետր: Այս երկու հատվածների հարաբերությունը կարելի է ներկայացնել  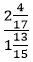կոտորակի տեսքով: Եթե այդ վախեցնող կոտորակի հայտարարն ու համարիչը բազմապատկենք 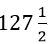-ով, կստանանք նույն հարաբերությունը` ամբողջ թվերի հարաբերության տեսքով, այսինքն :

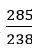(Ավելի հեշտ կլիներ տասնորդական կոտորակներից օգտվելը, սակայն Հին Հունաստանում դրանք հայտնի չէին: Եթե հետևենք այն ճանապարհին, որով հին մաթեմատիկոսները աշխարհն էին բացահայտում, մեր ճամփորդությունը զգալիորեն ավելի հետաքրքիր կլինի):

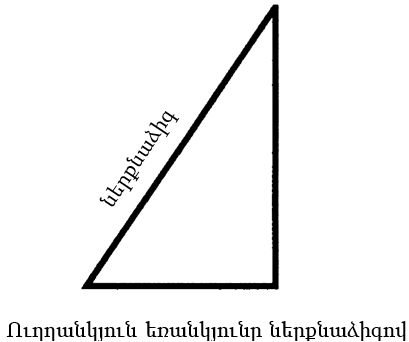Այժմ կարող ենք վերադառնալ մեր ուղղանկյանը: Մեզ հետաքրքրում է ուղղանկյան կողմերի և անկյունագծի երկարությունների հարաբերությունը, այսինքն՝ լուծում ենք նույն խնդիրը, ինչ ժամանակին հույն մաթեմատիկոսները: Քանի որ ուղղանկյունն անկյունագծով բաժանվում է երկու լրիվ համաչափ մասերի, կարող ենք հեշտացնել առաջադրանքը և դեն գցել մասերից մեկը, ասենք՝ ձախը։ Մնաց, այսպես կոչված, ուղղանկյուն եռանկյուն:

Դեռ շատ հարյուրամյակներ առաջ եգիպտացիները գործնականորեն պարզել են, որ եթե ուղղանկյուն եռանկյան մեկ կողմը հավասար է 3 միավորի, իսկ մյուսը՝ 4, ներքնաձիգի երկարությունը 5 միավոր կլինի: Տվյալ դեպքում ներքնաձիգի և կողմերից մեկի հարաբերությունը կլինի 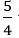 ավելի երկար կողմի համար և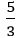ավելի կարճի համար:

Հույները խնդիրը ավելի ընդհանուր դիրքերից դիտարկեցին: Նրանց համար կարևորը օրինաչափություն գտնելն էր, այսինքն՝ ցանկացած ուղղանկյուն եռանկյան համար ուղղանկյան կողմերի երկարության և անկյունագծի երկարության հարաբերությունը:

Ինչպես փաստում է պատմությունը, հույն հայտնի մաթեմատիկոս Պյութագորասը այդպիսի օրինաչափություն հայտնաբերեց: Նա գտավ, որ ցանկացած ուղղանկյուն եռանկյան համար հետևյալ պնդումը ճիշտ է. կողմերի քառակուսիների գումարը հավասար է ներքնաձիգի քառակուսուն: Այս պնդումը ստացել է Պյութագորասի թեորեմ անվանումը: Թեորեմը մինչ այժմ կրում է մեծանուն հույնի անունը, չնայած այժմ գիտենք, որ Պյութագորասից դեռևս 600 տարի առաջ հին չինացիներին արդեն հայտնի էր այս հարաբերակցությունը:

Ստուգենք թեորեմը 3 և 4 կողմերով եռանկյան համար: Մի կողմի քառակուսին 3x3=9 է, մյուս կողմինը՝ 4х4=16: Քառակուսիների գումարը կլինի 9+16=25, այսինքն՝ ներքնաձիգի քառակուսին 25 է, հետևաբար, ներքնաձիգը 5 է:

Դիտարկենք ուրիշ եռանկյուն՝ 5 և 12 կողմերով:

Այս եռանկյան կողմերի քառակուսիների գումարը հավասար է 5х5+12х12=25+144=169: Հետևաբար, ներքնաձիգի քառակուսին 169 է: Ներքնաձիգը հավասար է 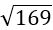, կամ 13, քանի որ 13х13=169: Այս եռանկյան համար ներքնաձիգի հարաբերությունը կողմին հավասար է 13/5՝ կարճ կողմի համար և 13/12՝ երկար կողմի համար։ 

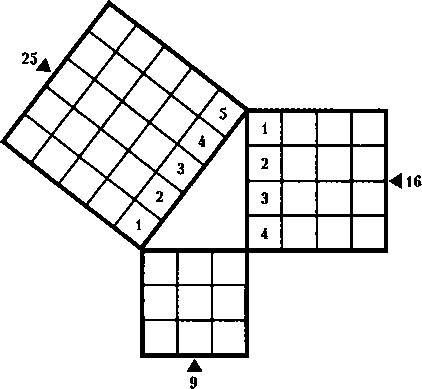
Պյութագորասի թեորեմը

Պյութագորասի թեորեմն օգտագործելով, կարելի է գտնել ներքնաձիգի և ուղղանկյուն եռանկյան ցանկացած կողմի հարաբերությունը: Հին Հունաստանի մաթեմատիկոսները կարող էին հանգիստ շունչ քաշել. խնդիրը լուծված էր: Ամենակարևորն այն է, որ թեորեմը տարածվում է բոլոր ուղղանկյուն եռանկյունների վրա, այդ թվում, բնականաբար, և հավասարասրուն, այսինքն՝ ուղղանկյուն եռանկյան, որի երկու կողմերը հավասար են:
Իսկ մեզ հիմա հենց այդպիսի եռանկյուններ են հետաքրքրում:
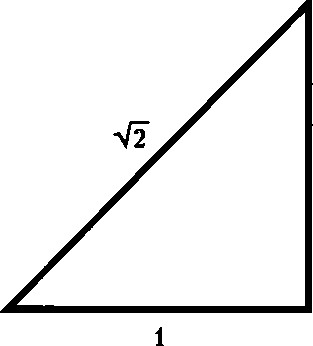
Դրանցից մեկը պատկերված է նկարում:

Առավել հեշտացնենք խնդիրը և ենթադրենք, որ եռանկյան կողմերը հավասար են 1-ի: Այդ դեպքում կողմի քառակուսին հավասար կլինի 1х1, իսկ կողմերի քառակուսիների գումարը՝ 1х1+1х1=2: Պյութագորասի թեորեմի համաձայն ներքնաձիգի քառակուսին հավասար է 2, իսկ ներքնաձիգը՝ համապատասխանաբար, √2:
Թվում է, թե հույներին շատ քիչ բան էր մնացել անելու: Պետք էր միայն գտնել այնպիսի կոտորակ, որը √2 է, իսկ հետո այն ամբողջ թվերի հարաբերության տեսքով ներկայացնել, և կարելի էր հաղթանակը տոնել: Սակայն ամեն ինչ ավելի բարդ ստացվեց:

Գոյություն չունեցող կոտորակներ

Այս գլխի սկզբում ցույց տվեցինք, որ 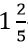-ը մոտ է -ին: Եթե այն ճշգրիտ հավասար լիներ -ի, խնդիրը լուծված կլիներ: Այդ ժամանակ 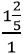 հարաբերությունը, որը կարելի է ամբողջ թվերի 7/5 հարաբերությամբ փոխարինել՝ կոտորակի վերին և ստորին հատվածները 5-ով բազմապատկելով, և կլինի փնտրվող մեծությունը:

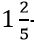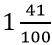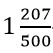Սակայն, դժբախտաբար, -ը -ի ճշգրիտ մեծությունը չէ: Ավելի ճշգրիտ պատասխան է , որն էլ 141/100 հարաբերությունն է: Էլ ավելի մեծ ճշտություն ենք ստանում, երբ -ը փոխարինում ենք -ով: Այս դեպքում ամբողջ թվերի հարաբերությունը կլինի 707/500: Բայց 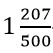–ն էլ 2-ի քառակուսի արմատի ճշգրիտ արժեքը չէ:

Հույն մաթեմատիկոսները շատ ժամանակ և ուժ են ծախսել -ի ճշգրիտ արժեքը հաշվելու համար, սակայն այդպես էլ դա նրանց չի հաջողվել: Նրանք չկարողացան 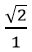 հարաբերությունը ամբողջ թվերի հարաբերության տեսքով ներկայացնել:

Վերջապես, հույն անվանի մաթեմատիկոս Էվկլիդեսն ապացուցեց, որ ինչքան էլ հաշվարկների ճշգրտությունը մեծացնենք, -ի ճշգրիտ արժեքը ստանալն անհնար է: Գոյություն չունի այնպիսի կոտորակ, որը քառակուսի բարձրացնելով՝ արդյունքում 2 ստացվի: Ասում են, որ այդպիսի եզրակացության առաջին անգամ հանգել է Պյութագորասը, սակայն այս անբացատրելի փաստն այնքան է շշմեցրել գիտնականին, որ նա ինքն իրեն երդվել է և իր աշակերտներից էլ այս հայտնագործությունը գաղտնի պահելու երդում է առել: Սակայն, հանրավոր է, այս տեղեկություններն իրականությանը չեն համապատասխանում:

Սակայն եթե 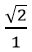 թիվը չի կարող ամբողջ թվերի հարաբերության տեսքով ներկայացվել, ապա  պարունակող ոչ մի կոտորակ, օրինակ 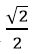 կամ 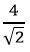նույնպես չեն կարող ամբողջ թվերի հարաբերության տեսքով ներկայացվել, քանի որ բոլոր այդպիսի կոտորակները կարող են ներկայացված լինել  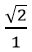-ի և ինչ-որ թվի արտադրյալի տեսքով: Այսպես, 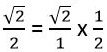: Կամ , որը կարելի է ձևափոխել, վերին և ստորին մասերը–ով բազմապատկելով, և կստանանք 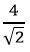: Պետք է չմոռանալ, որ անկախ նրանից, թե իրենից ինչ է ներկայացնում  թիվը, եթե այն բազմապատկենք -ով, 2 կստանանք)։

Քանի որ  թիվը հնարավոր չէ ներկայացնել ամբողջ թվերի հարաբերության տեսքով, այն ստացել է իռացիոնալ թիվ անունը: Մյուս կողմից, բոլոր թվերը, որոնք կարելի է ամբողջ թվերի հարաբերության տեսքով ներկայացնել, կոչվում են ռացիոնալ: Ռացիոնալ են բոլոր ամբողջ և կոտորակային թվերը՝ ինչպես դրական, այնպես էլ բացասական:

Պարզվեց, որ քառակուսի արմատների մեծ մասը իռացիոնալ թվեր են: Ռացիոնալ քառակուսի արմատեր ունեն միայն քառակուսային թվերի շարքում եղածները, որոնց մասին խոսել ենք վեցերորդ գլխում: Այս թվերն անվանում են նաև լրիվ քառակուսիներ: Այս լրիվ քառակուսիներից կազմված կոտորակները նույնպես ռացիոնալ թվեր են:

Օրինակ, 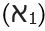 ռացիոնալ թիվ է, քանի որ 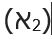կամ 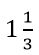 (4-ը 16-ից քառակուսի արմատ է, իսկ 3-ը՝ 9-ից):

Փաստը, որ շատ քառակուսի արմատներ իռացիոնալ թվեր են, ամենևին չի արժեզրկում նրանց նշանակությունը, մասնավորապես,  թիվը շատ հաճախ են օգտագործում տարբեր ինժեներական և գիտական հաշվարկներում: Այս թիվը կարելի է հաշվել այն ճշգրտությամբ, որն անհրաժեշտ է յուրաքանչյուր դեպքում: Հաշվարկման եղանակը նկարագրված էր այս գլխի սկզբում, և կարող եք այդ թիվը ստանալ զրոյից այնքան թվանշանների քանակով, որքան համբերություններդ կների:

Օրինակ,  թիվը կարելի է որոշել մինչև վեց տասնորդական նիշի ճշտությամբ՝ =1,414214: Այս մեծությունն այնքան շատ չի տարբերվում իրական արժեքից, քանի որ 1,414214х1,414214=2,000001237796: Այս պատասխանը 2-ից տարբերվում է հազիվ մեկ միլիոներորդը գերազանցող մեծությամբ: Այդ պատճառով  համար 1,414214 արժեքը գործնական խնդիրների մեծամասնության համար լիովին ընդունելի է: Այն դեպքում, երբ ավելի մեծ ճշտություն է պահանջվում, դժվար չէ ստորակետից հետո այնքան նշանակալի նիշեր ստանալ, որքան տվյալ դեպքում անհրաժեշտ է:

Սակայն եթե դուք հազվադեպ հանդիպող համառություն դրսևորեք և փորձեք -ից այնքան ժամանակ քառակուսի արմատ հանել, մինչև ճշգրիտ արդյունքի հասնեք, դուք երբեք չեք ավարտի ձեր աշխատանքը: Դա անվերջանալի գործընթաց է: Ստորակետից հետո ինչքան էլ տասնորդական նիշ ստանաք, միշտ էլի հաջորդները կմնան:

Այս փաստը կարող է ձեզ զարմացնել նույնքան ուժգին, որքան 1/3-ի՝ 0,333333333...... անվերջ տասնորդական կոտորակի փոխակերպումը, կամ 1/7-ի փոխակերպումը 0,142857142857142857... և այսպես անվերջ: Առաջին հայացքից կարող է թվալ, որ այս անվերջ տասնորդական կոտորակները և իռացիոնալ քառակուսի արմատները միևնույն կարգի դրսևորումներ են, բայց դա այդպես չէ: Այդ անվերջ կոտորակները կոտորակային համարժեք ունեն, մինչդեռ  -ը այդպիսի համարժեք չունի: Իսկ ինչո՞ւ: Բանն այն է, որ1/3-ի և1/7-ի տասնորդական համարժեքները, ինչպես նաև անվերջ թվով ուրիշ կոտորակներինը, անվերջ պարբերական կոտորակներ են:

Մինչդեռ  –ի տասնորդական համարժեքը ոչ պարբերական կոտորակ է։ Այս պնդումը ճշմարիտ է նաև ցանկացած իռացիոնալ թվի համար:

Խնդիրն այն է, որ ցանկացած տասնորդական կոտորակ, որը 2-ից քառակուսի արմատի մոտավոր արժեքն է, ոչ պարբերական կոտորակ է: Հաշվարկներում ինչքան էլ հեռու գնանք, ցանկացած կոտորակ, որը կստանանք, ոչ պարբերական կլինի:

Պատկերացրեք ստորակետից հետո հսկայական քանակի ոչ պարբերական թվանշաններով կոտորակ: Եթե հանկարծ միլիոներորդ թվից հետո տասնորդական նիշերի ամբողջ հաջորդականությունը կրկնվի, նշանակում է, տասնորդական կոտորակը պարբերական է, և նրա համար գոյություն ունի ամբողջ թվերի հարաբերության տեսքով համարժեք: Եթե հսկայական քանակի (միլիարդավոր կամ միլիոնավոր) ոչ պարբերական տասնորդական նիշեր ունեցող կոտորակի մոտ ինչ-որ պահ հայտնվում է կրկնվող թվանշանների անվերջ շարք, օրինակ...55555555555..., նշանակում է, որ տվյալ կոտորակը պարբերական է և նրա համար գոյություն ունի ամբողջ թվերի հարաբերության տեսքով համարժեք:

Սակայն, իռացիոնալ թվերի դեպքում նրանց տասնորդական համարժեքները լրիվ ոչ պարբերական են և չեն կարող փոխակերպվել պարբերականի: (Բնականաբար, կարող եք ինձ հետևյալ հարցը տալ. «Իսկ ո՞վ կարող է հաստատ իմանալ և ասել, տրիլիոն նիշից հետո կոտորակի հետ ինչ է կատարվում: Ո՞վ կարող է երաշխավորել, որ կոտորակը պարբերական չի դառնա»: Գոյություն ունեն անհերքելիորեն ապացուցելու եղանակներ, որ իռացիոնալ թվերը պարբերական չեն, բայց այդպիսի ապացույցները բարդ մաթեմատիակական ապարատ են պահանջում, այդ պատճառով էլ չենք կարող մեր գրքում այն քննարկել: Սակայն, եթե հանկարծ պարզվի, որ իռացիոնալ թվերը պարբերական կոտորակներ են դառնում, դա կնշանակի մաթեմատիակական գիտությունների հիմնովին փլուզում: Իրականում դա հազիվ թե հնարավոր է):

Կոտորակների գոյությունը

Այժմ դիտարկենք (2⁴)² արտահայտությունը: Այս գրառումը նշանակում է, որ 2⁴ պետք է քառակուսի բարձրացնել: 2⁴ թիվը 2х2х2х2-ն է, կամ 16-ը: Այնուհետև, 16-ի քառակուսին՝ 16х16-ն է, կամ՝ 256: Այսպիսով, (2⁴)²=256: Սակայն 256-ը նույն է, ինչ 2х2х2х2х2х2х2х2,կամ 2⁸: Հետևաբար, (2⁴)²=2⁸:

Եթե նման գործողություններ կատարեք տարբեր, ինչպես հիմքով, այնպես էլ աստիճանացույցերով տարբերվող, աստիճանային արտահայտություններով, կարող եք համոզվել, որ բոլոր աստիճանային արտահայտությունների համար գոյություն ունի կանոն. աստիճանային թիվն աստիճան բարձրացնելիս աստիճանացույցերը բազմապատկվում են: Սա նշանակում է, որ հաշվարկներ չկատարելով՝ միշտ կարող ենք ասել հետևյալը, որ (З⁵)² = З¹⁰, իսկ (7⁸)⁷ = 7⁵⁶ և այլն:

Եթե այս պնդումը ճիշտ է, ապա, ակնհայտ է, որ այն ճիշտ կլինի նաև կոտորակային աստիճանացույցի համար: Դիտարկենք 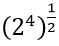 թիվը: Հետևելով աստիճանացույցների բազմապատկման կանոնին, կստանանք 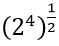=2². Այնուհետև, քանի որ 2⁴=16, իսկ 2²=4, ապա կարող են պնդել, որ 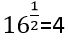=4 : Սակայն գիտենք նաև, որ 4-ը 16-ի քառակուսի արմատն է, նշանակում է, թիվը 1/2 աստիճան բարձրացնելը համարժեք է այդ թվից քառակուսի արմատ հանելուն: Այլ կերպ ասած, 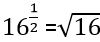: Հետևելով այս կանոնին, կարելի է պնդել, որ 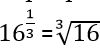,  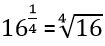և այլն: Այժմ գործածության մեջ դրեցինք կոտորակային աստիճանացույցերը, որոնց մասին խոստացել էի պատմել դեռևս վեցերորդ գլխում: Ուշադրություն դարձրեք, որ  –ը վերջավոր կոտորակի տեսքով հնարավոր չէ ներկայացնել, սակայն կոտորակային աստիճանացույցով աստիճանային արտահայտության տեսքով կարելի է: Ի՞նչ է կոտորակային ցուցիչով աստիճանը: Օրինակ, 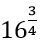 արտահայտությունը նույնն է, ինչ 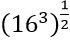, քանի որ 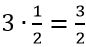: Հետևաբար, 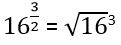: Կամ, ընդհանրացնելով, կարելի է ասել, որ կոտորակային աստիճանացույցի դեպքում հիմքը աստիճանացույցի համարիչին հավասար աստիճան է բարձրացվում, և նրանից աստիճանացույցի հայտարարին հավասար արմատ է հանվում: Հետևաբար, 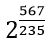–ը 235 աստիճանի արմատն է, 2-ի 567 աստիճանից:

Ակնհայտ է, որ կոտորակային ցուցիչով աստիճանները շատ դժվարմարս են: Իսկ չի կարելի՞ անցում կատարել տասնորդական կոտորակների: Հիշում ենք, որ 1/2-ը 0,5-ն է, այնպես որ 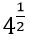 փոխարեն կարելի է գրել 4^0,5:

Ցանկացած տասնորդական աստիճան իր նշանակությունն ունի: Օրինակ, 2^5,175-ը 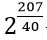-ն է, քանի որ 5,175=207/40: Իր հերթին,  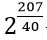թիվն ստացվում է 2-ը 207 աստիճան բարձրացնելու և ստացված թվից 40 աստիճանի արմատ հանելու արդյունքում (Կարելի է գործողությունների տեղերը փոխել: Եթե սկզբում 2-ից 40 աստիճանի արմատ հանենք, հետո այդ միջանկյալ արդյունքը բարձրացնենք 207 աստիճան, կստանանք միևնույն վերջնական արդյունքը): Այս պնդումը կարող եք հեշտությամբ ստուգել ավելի պարզ օրինակի վրա, օրինակ՝  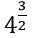արտահայտության համար: Քառակուսի արմատ 4³-ից 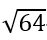-ն է, որն էլ հավասար է 8: Միևնույն ժամանակ 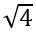խորանարդը հավասար է 2³, որը նույնպես հավասար է 8:

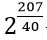 արտահայտության արժեքը (կամ ցանկացած այլ արտահայտության, որտեղ աստիճանացույցը ամբողջ, կոտորակային, տասնորդական, դրական կամ բացասական թիվ է) համապատասխան մաթեմատիկական մեթոդներով կարելի է հաշվել:

Ընդ որում, ստիպված չեք լինի երկու հարյուր յոթ անգամ 2 բազմապատկել կամ հաջորդական մոտարկումների եղանակով փնտրել քառասուն աստիճանի արմատի մոտավոր արժեքը: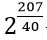=36,126։ Այս մեծությունը մոտավոր է, քանի որ 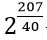-ը իռացիոնալ թիվ է, ինչպես կոտորակային կամ տասնորդական աստիճանացույցերով արտահայտությունների մեծամասնությունը: 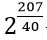–ի տասնորդական համարժեքը ոչ պարբերական անվերջ կոտորակ է, սակայն միշտ կարող ենք ստորակետից հետո ստանալ այնքան տասնորդական նիշ, որքան պահանջվում է կոնկրետ հաշվարկի ճշգրտության համար:

Օգտագործելով ցանկացած թիվ որպես աստիճանային արտահայտության հիմք՝ կարող ենք կազմել համապատասխան աստիճանային արտահայտությունը ցանկացած ուրիշ թվի համար: Այժմ կարող ենք վերադառնել 7х17 բազմապատկան խնդրին, որը հանդիպեց դեռևս վեցերորդ գլխում: 7 թիվը կարելի է ներկայացնել ինչպես 2^2,81, կամ 3^1,77 կամ 5^1,21 (աստիճանային համարժեքները հաշվարկելու համար հատուկ մեթոդներ կան), միևնույն ժամանակ 17-ը հավասար է 2^4,08, З^2,58 կամ 5^1,76: Այժմ բազմապատկան խնդիրը կարելի է հանգեցնել գումարման՝ 7x17=2^2,81х2^4,08=2^2,81+4,08=2^6,89, կամ З^1,77хЗ^2,58=З^4,35, կամ 5^1,21х5^1,76=5^2,97: Բոլոր այս թվերը՝ 2^6,89, З^4,35, 5^2,97, մոտավորապես հավասար են միմյանց և մոտավորապես հավասար են 119, սա էլ հենց պատասխանն է:

Իհարկե, ավելի հեշտ կլիներ աստիճանային արտահայտությունների արժեքները գտնելու փոխարեն, ուղղակի 7 х 17 բազմապատկել: Բացի դրանից, ճշգրիտ պատասխանի փոխարեն ստացանք մոտավորը: Սակայն եկեք տեսնենք, թե հետո ինչ կլինի: Հնարավոր է, որ այս մեթոդն անփոխարինելի լինի: Ուշադրություն դարձնենք աստիճանային արտահայտությունների հիմքերին: Ընտրել ենք 2, 3 կամ 5: Իսկ ինչո՞ւ 10 թիվը չընտրենք, չէ՞ որ 10–ը մեր հաշվարկման համակարգի հիմքն է: