Ենթադրություն և գիտական մեթոդ
Primary tabs
Մաթեմատիկական հայտնություն
Գլուխ 15
Ոչ մաթեմատիկական ինդուկցիան էական դեր է խաղում մաթեմատիկական հետազոտություններում։
Իսայ Շուր, Դիսերտացիա, 1901, I մաս
Գիտելիքի ցանկացած բնագավառում դժվար է ճշմարտությանը բավականաչափ մոտ նկարագրել մեթոդը, որին հետևել է առաջին բացահայտողը...
Այնուամենայնիվ, քանի որ սա վերաբերում է մաթեմատիկական ստեղծագործությանը, կարելի մի պարզ դիտողություն անել, ինչը բազմաթիվ անգամներ հաստատել է գիտության պատմությունը. դիտարկումը կարևոր տեղ ունի և մեծ դեր է խաղում այս պրոցեսում:
Շարլ Հերմիտ, Oeuvres, Փարիզ, 1905 — 1917, հ. IV, էջ 586
Դիտարկումները հայտնագործությունների առատ աղբյուր են ինչպես սուբյեկտիվ երևույթների, այնպես էլ մեր զգայարաններով ընկալվող իրական երևույթների աշխարհում:
Շարլ Հերմիտ, Գրագրություն Ստիլտյեսի հետ, Փարիզ, 1905, հ. I, էջ 332
§1. Գիտա-հետազոտական աշխատանքը միջնակարգ դպրոցի մակարդակում
Մաթեմատիկայի ուսուցումը պետք է նախատեսի սովորողների ծանոթացումը (հասկանալի է, որ թույլատրելի սահմաններում) մաթեմատիկական գործունեության բոլոր կողմերին: Հատկապես կարևոր է, որ ինքնուրույն ստեղծագոծական աշխատանքի ճանապարհ բացի, իհարկե, հնարավորի սահմաններում:
Սակայն մասնագետ-մաթեմատիկոսի գործունեությունը շատ խիստ և շատ կողմերից տարբերվում է դասարանում սովորողների պարապմունքներից: Այս տարբերություններից ո՞րն է հատուկ ուշադրության արժանի: Այս հարցին կպատասխանենք մի քանի օրինակների ծանոթանալուց հետո: Դրանք ցույց կտան, որ լավ ուսուցիչը, ընտրելով հարմար խնդիրներ և դրանք մատուցելով համապատասխան ձևով, նույնիսկ միջին դասարանին կարող է առաջարկել ինքուրույն հետազոտությանը մոտ ինչ-որ բան:
§2. Օրինակ
«Հավասարասրուն ուղղանկյուն եռանկյան տրված P պարագծով հաշվեք նրա S մակերեսը»: Սովորական խնդրագրքերում հենց այսպիսի խնդիրներ են հանդիպում: Ընդհանուր առմամբ, սա վատ խնդիր չէ, միայն թե բավարար չափով հետաքրքիր չէ, եթե առանձին է ներկայացվում՝ նմանատիպ խնդիրներից առանձին: Համեմատեք ստորև բերված մատուցման ձևը սովորականի հետ և ուշադրություն դարձրեք տարբերությանը։
«Տափաստանները յուրացնելու առասպելական ժամանակներում,- ասում է ուսուցիչը,- երբ հողը շատ-շատ էր, իսկ մնացած ամեն ինչը հազիվ էր բավականացնում, Միջին Արևմուտքի ցանկացած բնակիչ շատ արոտավայր ուներ, բայց միայն հարյուր յարդ մետաղալար: Նա իր ունեցած ամբողջ մետաղալարով ցանկանում էր հողակտոր առանձնացնել: Մտորելով հողակտորնորի տարբեր ձևերի մասին, նա զարմացավ, թե որքան փոքր կտոր կարող է առանձնացնել: Եվ ահա, հողակտորի ի՞նչ ձև կնախընտրեիք: Բայց չմոռանաք, որ պետք է նրա մակերեսը հաշվեք, այնպես որ, ավելի լավ է ընտրեք մի պարզ պատկեր»:
- Քառակուսի:
- Ուղղանկյուն՝ 20 և 30 յարդանոց կողմերով:
- Հավասարակողմ եռանկյուն:
- Հավասարասրուն ուղղանկյուն եռանկյուն:
- Շրջան:
«Շատ լավ: Կարող եմ ես էլ մի քանի պատկեր ավելացնել՝ 10 և 40 յարդանոց կողմերով ուղղանկյուն, 42, 29 և 29 կողմերով հավասարասրուն եռանկյուն, 42, 13, 32, 13 կողմերով հավասարասրուն սեղան, կանոնավոր վեցանկյուն, կիսաշրջան»:
«Այս բոլոր պատկերները հավասրապարագիծ են, այսինքն, այնպիսին, որոնց պարագծերը հավասար են միմյանց. առաջարկվող խնդրում այն հարյուր յարդ էր: Քառակուսի յարդերով հաշվեք նշված պատկերների մակերեսները և դասավորեք նվազման կարգով: Նախքան մակերեսները հաշվելը, կարող եք փորձել գուշակել, թե որը կունենա ամենամեծ մակերես, որը՝ ամենափոքր»:
Այս խնդիրը կարելի առաջադրել միջին առաջադիմությամբ դասարանին, եթե միայն աշակերտների գիտելիքները բավարարում են»: Ահա խնդրի լուծումը աղյուսակի տեսքով.
|
Պատկերը |
Մակերեսը (որոշ դեպքերում մոտավոր) |
|
Շրջան |
795 |
|
Կանոնավոր վեցանկյուն |
722 |
|
Քառակուսի |
625 |
|
30x20 ուղղանկյուն |
600 |
|
Կիսաշրջան |
594 |
|
Հավասրակողմ եռանկյուն |
481 |
|
42, 13, 32, 13 կողմերով սեղան |
444 |
|
Հավասարակողմ ուղղանկյուն եռանկյուն |
430 |
|
42, 29, 29 կողմերով եռանկյուն |
420 |
|
40x10 չափսի ուղղանկյուն |
400 |
«Էլի հարցեր կա՞ն»:
§3. Քննարկում
Մեր հիմնական նպատակը սովորողների ուշադրությունը պատկերների և նրանց մակերեսների այդ ցուցակին հրավիրելն է. այս աղյուսակի զննումը սովորողների՝ նկատառումների շարք պետք է առաջացնի: Ուսուցիչը այստեղ որքան քիչ հուշի, այնքան լավ: Եթե հապաղում են, ուսուցիչը կարող է քննարկումը աշխուժացնել՝ զգուշորեն հուշող հարցեր տալով, օրինակ այսպիսին.
«Ի՞նչ կարող եք ասել այս ցուցակի մասին»:
«Ցուցակում առաջին տեղում շրջանն է։ Ի՞նչ եք մտածում այս մասին»:
«Ցուցակում մի քանի եռանկյուններ և քառանկյուններ կան: Քառանկյուններից ո՞րն է ավելի առաջ մյուսներից: Իսկ ինչպե՞ս է վիճակը եռանկյունների դեպքում»:
«Այո, հնարավոր է, որ դուք ճիշտ եք, բայց դա ապացուցե՞լ եք»:
«Եթե դա չեք ապացուցել, ի՞նչ հիմքեր ունեք դրանք ճիշտ համարելու»:
«Եռանկյունը կարելի է դիտարկել որպես այլափոխված քառանկյուն, որի մի կողմը 0 է (կամ անկյուններից մեկը 1800 է): Կօգնի ձեզ այս դիտարկումը»:
Ի վերջո, շուտ թե ուշ և հնարավորին չափ ինքնուրույն, սովորողները պետք է գան հետևյալ եզրակացություններին.
Մեր ցուցակը հուշում է, որ.
- հավասար պարագիծ ունեցող բոլոր հարթ պատկերներից ամենամեծ մակերես շրջանն ունի.
- հավասար պարագիծ ունեցող քառանկյուններից ամենամեծ մակերեսը քառակուսին ունի.
- հավասար պարագիծ ունեցող բոլոր եռանկյուններից ամենամեծ մակերես ունի հավասարակողմ եռանկյունը.
- կողմերի տրված n քանակը և նույն պարագիծն ունեցող բոլոր բազմանկյունների մեջ ամենամեծ մակերես ունի կանոնավորը:
Այս ցուցակը ուսումնասիրով կարելի հանգել եզրակացության, որ եթե երկու կանոնավոր բազմանկյուններ հավասար պարագծեր ունեն, ավելի մեծ մակերես կունենա այն բազմանկյունը, որի կողմերի քանակը ավելի մեծ է: (Ինչքան բազմանկյունը մոտ է շրջանի, հավանաբար, նրա մակերեսը այնքան մեծ է)։
Ասված պնդումներից ոչ մեկը չի ապացուցվում մեր ցուցակով, չնայած, այն կարող է որոշակի հիմք լինել, որպեսզի այդ պնդումներին հավատանք (հասկանալի է, ավելի կամ պակաս չափով):
Փորձը կարող է ավելի ընդհանուր դատողությունների բերել այս պնդումների մասին. օրինակ՝ պնդման ճշմարտացի լինելը ավելի շատ դեպքերի համար լուրջ փաստարկ է նրա ճշմարիտ լինելու համար:
Մեր ցուցակից կարելի է էլի շարք եզրակացություններ անել, ընդ որում օրինակների քանակի մեծացնելը կխթանի նոր վարկածների առաջացումը:
§4. Էլի լի օրինակ
«Հին հույները,- ասում է ուսուցիչը,- եռանկյան մակերեսի մասին հիանալի առաջադրություն գիտեին, որը հիմա հայտնի է Հերոնի բանաձև անունով և արտահայտվում է S2=p(p-a)(p-b)(p-c) բանաձևով, որտեղ S–ը եռանկյան մակերեսն է, а, b և с-ն նրա կողմերը, իսկ 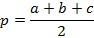 կիսապարագիծը:
կիսապարագիծը:
Հերոնի բանաձևի ապացույցը այնքան էլ հեշտ չէ, և այսօր մտադիր չեմ դրանով զբաղվելու: Սակայն, առանց ապացույցի չենք կարող վստահ լինել, որ հավասարությունը ճիշտ է գրված. այս բանաձևը գրելիս հիշողությունս կարող էր դավաճանել ինձ: Կարո՞ղ եք ստուգել այս բանաձևը: Ինչպե՞ս կարելի է վարվել»:
- Ստուգենք հավասարակողմ եռանկյան դեպքում:
Այս դեպքում а=b=с, 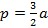 , և բանաձևը ճիշտ արդյունք է տալիս:
, և բանաձևը ճիշտ արդյունք է տալիս:
«Էլ ի՞նչ կարող ենք անել»:
- Եկեք ուղղանկյուն եռանկյան դեպքը ստուգենք:
- Եկեք հավասարասրուն եռանկյան դեպքը ստուգենք:
Առաջին դեպքում с2=а2+b2, երկրորդ դեպքում а=b և երկու դեպքում էլ (այստեղ մեզ որոշակի հանրահաշվական ձևափոխություններ պետք կլինեն) բանաձևը ճիշտ արդյունք է տալիս: (Ընթերցողին խուրհուրդ ենք տալիս այդ ձևափոխությունները կատարել):
«Դե, սա ձեզ դուր եկա՞վ»:
- Այո, բանաձևը վստահության արժանի է:
«Կարո՞ղ եք ուրիշ մասնավոր դեպք մտածել, որը օրինակ կարող է ծառայել»:
«Ի՞նչ կարծիք ունեք այլափոխված եռանկյան մասին: Նկատի ունեմ եռանկյան սահմանային դեպքը, երբ այն վեր է ածվում հատվածի»:
Այդ դեպքում р=с (կամ а, կամ b), և մեր բանաձևը, ակնհայտորեն, ճիշտ արդյունք է տալիս:
- Ուսուցիչ. խնդրում եմ ասեք, թե քանի ստուգում պետք է անել համոզվելու համար, որ բանաձևը ճիշտ է:
Ընթերցողը կարող է երևակայել վերջին հարցից սկսվող բանավեճ:
§5. Ինդուկտիվ դատողության գրաֆիկական պատկերումը
Ի՞նչի հասանք և ինչի՞ չհասանք 4–րդ պարագրաֆում Հերոնի բանաձևի վերջին մի քանի ստուգումների արդյունքում: Յուրաքնաչյուր ստուգում վերաբերում էր որոշակի տեսակի եռանկյան, այդ պատճառով էլ հարցը կարող է լուծվել բոլոր հնարավոր ձևի եռանկյունները դիտարկելով:
Դիցուք, եռանկյան կողմերն են х, у և z, որոնք գրված են աճման կարգով, այսինքն՝ 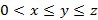 ։
։
Ընդ որում պարտադիր է, որ x+y>z:
Քանի որ մեզ համար կարևոր է միայն եռանկյան ձևը, այլ ոչ չափսերը, կարելի է համարել, որ z=1։
Այսպիսով, երեք անհավասարություն ունենք. 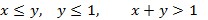
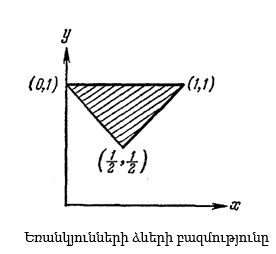 Հիմա դիտարկենք x, y, 1 կողմերով եռանկյուն, կարճ ասած, (x, y, 1) եռանկյուն, հարթության (x, y) կետով (որտեղ x, y-դեկարտյան կոորդինատներ են): Երեք անհավասարությունները՝ միասին դիտարկելով բնորոշում են երեք կիսահարթությունների ընդհանուր մասով կամ հատումով որոշված կետերի բազմությունը: Այդ հատումը (1, 1), (0, 1) և
Հիմա դիտարկենք x, y, 1 կողմերով եռանկյուն, կարճ ասած, (x, y, 1) եռանկյուն, հարթության (x, y) կետով (որտեղ x, y-դեկարտյան կոորդինատներ են): Երեք անհավասարությունները՝ միասին դիտարկելով բնորոշում են երեք կիսահարթությունների ընդհանուր մասով կամ հատումով որոշված կետերի բազմությունը: Այդ հատումը (1, 1), (0, 1) և 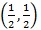 գագաթներով եռանկյուն է (տես նկարը, որը պարունակում է (1, 1) գագաթը, նրանից ելնող երկու կողմերը, բայց չի պարունակում մյուս երկու գագաթները և երրորդ կողմը). այն իրենից ներկայացնում է տարբեր ձևի եռանկյունների ամբողջությունը, իսկ առանձին (x, y) կետը՝ առանձին (x, y, 1) եռանկյուն, ընդ որում տարբեր կետեր ներկայացնում են տարբեր ձևի եռանկյուններ:
գագաթներով եռանկյուն է (տես նկարը, որը պարունակում է (1, 1) գագաթը, նրանից ելնող երկու կողմերը, բայց չի պարունակում մյուս երկու գագաթները և երրորդ կողմը). այն իրենից ներկայացնում է տարբեր ձևի եռանկյունների ամբողջությունը, իսկ առանձին (x, y) կետը՝ առանձին (x, y, 1) եռանկյուն, ընդ որում տարբեր կետեր ներկայացնում են տարբեր ձևի եռանկյուններ:
 Նկարի ո՞ր կետերն են համապատասխանում 4-րդ պարագրաֆում դիտարկված մասնավոր դեպքերին: Սկզբում Հերոնի բանաձևը ստուգեցինք հավասարակողմ եռանկյան համար: Այդ եռանկյանը համապատասխանում է (1, 1, 1) նշանակումը, որը նկարում պատկերված է (1,1) կոորդինատներ ունեցող կետով: Հետո այդ բանաձևը ստուգեցինք ուղղանկյուն եռանկյան համար: Եթե (х, у, 1)-ը ուղղանկյուն եռանկյուն է, նրա մեծ կողմը՝ 1-ը կլինի ներքնաձիգը և x2 +y2=1:
Նկարի ո՞ր կետերն են համապատասխանում 4-րդ պարագրաֆում դիտարկված մասնավոր դեպքերին: Սկզբում Հերոնի բանաձևը ստուգեցինք հավասարակողմ եռանկյան համար: Այդ եռանկյանը համապատասխանում է (1, 1, 1) նշանակումը, որը նկարում պատկերված է (1,1) կոորդինատներ ունեցող կետով: Հետո այդ բանաձևը ստուգեցինք ուղղանկյուն եռանկյան համար: Եթե (х, у, 1)-ը ուղղանկյուն եռանկյուն է, նրա մեծ կողմը՝ 1-ը կլինի ներքնաձիգը և x2 +y2=1:
 Այստեղից հետևում է, որ ուղղանկյուն եռանկյունները գծագրի վրա պատկերվում են շրջանագծի (միավոր) աղեղով:
Այստեղից հետևում է, որ ուղղանկյուն եռանկյունները գծագրի վրա պատկերվում են շրջանագծի (միավոր) աղեղով:
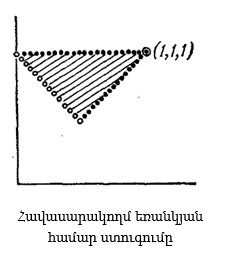
Այնուհետև դիտարկեցինք հավասրասրուն եռանկյունները: Այստեղ երկու դեպք պետք է տարբերենք. առաջինը՝ եռանկյուններ, որոնց երկար կողմերն են հավասար, և հետևաբար y=1, և երկրոդ՝ եռանկյուններ, որոնց կարճ կողմերն են իրար հավասար, այսինքն՝ երբ x=y։
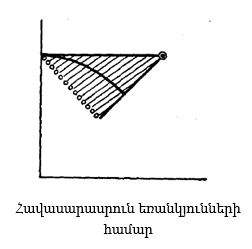 Այստեղից հետևում է, որ հավասարասրուն եռանկյուններ ներկայացնող կետերը գծագրի վրա լցնում են երկու սահմանային հատվածները (այս գծագրի վրա՝ հոծ գծեր, որոնք նախորդ գծագրերի վրա կետերով էին պատկերված):
Այստեղից հետևում է, որ հավասարասրուն եռանկյուններ ներկայացնող կետերը գծագրի վրա լցնում են երկու սահմանային հատվածները (այս գծագրի վրա՝ հոծ գծեր, որոնք նախորդ գծագրերի վրա կետերով էին պատկերված):
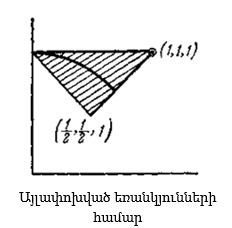 Վերջապես, այլափոխված (х, у, 1) եռանկյունների համար («զրոյական մակերեսով եռանկյուններ»). x+y=1:
Վերջապես, այլափոխված (х, у, 1) եռանկյունների համար («զրոյական մակերեսով եռանկյուններ»). x+y=1:
Այդ եռանկյունները պատկերված են երրորդ սահմանային հատվածով, որը գծագրի վրա պատկերված է հոծ գծով (նախորդ նկարների վրա այն նշված էր սպիտակ կետերով):
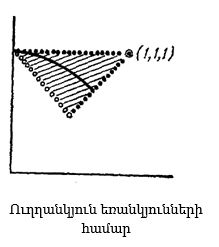
Ուսումնասիրելով գծագրերը՝ կարող ենք մեզ համար տեսանելի պատկերացնել ինդուկտիվ դատողության զարգացումը: Սկզբում ստուգելու աստիճանը պատկերելու համար բավական էր մեկ կետը: Հետո գծագրի վրա ավելանում են ավելի և ավելի շատ հոծ գծեր, որոնք ներկայացնում են ստուգումներում ընդգրկված ավելի ու ավելի նոր դեպքեր:
Հատուկ տեսակի եռանկյուններին, որոնց համար ստուգել ենք Հերոնի բանաձևը, համապատասխանող կետերը տեղադրվում են գծերի վրա: Սակայն բանաձևը մնում է չստուգված ընդհանուր տեսքի եռանկյունների «հիմնական զանգվածի» համար, որոնք պատկերվում են այդ գծերով սահմանափակված տիրույթների ներքին կետերով: Ամեն դեպքում, այստեղ կարելի է նկատել՝ քանի որ բանաձևը ճիշտ էր եռանկյունը սահմանափակող գծերի բոլոր կետերի, ինչպես նաև այդ տիրույթը հատող գծի կետերի համար, բնական է հուսալ, որ այն ճիշտ կլինի նաև մնացած կետերի համար: Մասը հուշում է ամբողջը, և բավականին համոզիչ է հուշում:
§6. Մի օրինակ պատմությունից
Այստեղ կդիտարկենք մի տարածաչափական խնդիր: Ընդ որում կգնանք երկու խոշոր մաթեմատիկոսների հետքերով. նրանց անունները ավելի ուշ կհայտնեմ, թե չէ պատմությանս ազդեցությունը մասնակիորեն կկորչի:
1°. Նմանանությունը հարց է հուշում. բազմանիստը սահմանափակված է հարթ նիստերով, ինչպես բազմանկյունը սահմանափակված է ուղղի հատվածներով: Տարածության մեջ բազմանիստի և հարթության վրա բազմանկյան անալոգիան ակնհայտ է: Սակայն բազմանկյուններն ուսումնասիրելը ավելի հեշտ և մատչելի է, քան բազմանիստները. կարելի է սպասել, որ բազմանկյունների վերաբերող ցանկացած հարց շատ ավելի հեշտ կլինի, քան համապատասխան տարածաչափական հարցը, որը վերաբերում է բազմանիստների հատկություններին: Բազմանկյուններին վերաբերող ինչ-որ փաստ նկատելուց հետո պետք է փորձենք նմանատիպ հանգամանք գտնել բազմանիստների համար. ընդ որում լավ հնարավորություն կունենանք ուսանելի ինչ-որ բան հայտնաբերելու համար: Օրինակ, հայտնի է, որ եռանկյան ներքին անկյունների գումարը նույնն է բոլոր եռանկյունների համար և կախված չէ ո՛չ եռանկյան ձևից, ո՛չ չափսերից, և հավասար է 180o, կամ երկու ուղիղ անկյան, կամ 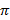 (ռադիանային միավորներով. հետագայում անկյունների չափման համար կգերադասենք հենց այս միավորը): Ավելի ընդհանուր պնդում է, որ n-անկյան անկյունների գումարը (n-2)
(ռադիանային միավորներով. հետագայում անկյունների չափման համար կգերադասենք հենց այս միավորը): Ավելի ընդհանուր պնդում է, որ n-անկյան անկյունների գումարը (n-2)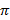 է: Չկա՞ նմանատիպ ինչ-որ բան բազմանիստների համար:
է: Չկա՞ նմանատիպ ինչ-որ բան բազմանիստների համար:
2°. Ձգտում ենք սպառել բոլոր հնարավորությունները. Մեր նպատակը դեռևս այնքան էլ պարզ չէ: Ցանկանում ենք ինչ-որ բան իմանալ բազմանիստի անկյունների գումարի մասին, բայց ի՞նչ անկյուններ նկատի ունենք: Բազմանիստի յուրաքանչյուր կողին երկնիստ անկյուն է համապատասխանում, որը կազմված է այդ կողով հատվող նիստերով: Բազմանիստի յուրաքանչյուր գագաթի մարմնային անկյուն է համապատասխանում՝ կազմված այդ գագաթում հատվող նիստերով (երեք կամ ավելի): Ո՞ր անկյունները արժի քննարկել: Այս կամ այլ տեսակի անկյունների գումարն ունի՞ ինչ-որ պարզ հատկություն: Ինչպիսի՞ն է վիճակը, օրինակ քառանիստի վեց երկնիստ անկյունների գումարի համար: Իսկ ի՞նչ կարելի ասել նրա չորս մարմնային անկյունների համար:
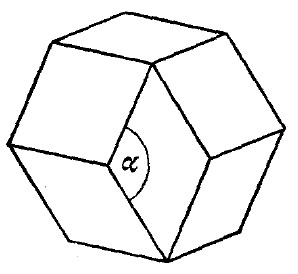 Պարզվում է որ այդ գումարներից ոչ մեկը անկախ չէ քառանիստի ձևից (տես օրինակ 15-ը): Ի՜նչ հիասթափություն: Չէինք սպասում, որ քառանիստը իրեն այդպես վատ կպահեր. կարծում էինք, թե այն նման է եռանկյանը: Սակայն, հավանաբար, ամեն ինչ դեռ կորած չէ, քանի որ դեռ բոլոր հնարավորությունները չեն սպառվել: Բազմանիստը, բացի դիտարկվածներից, ունի նաև այլ տեսակի անկյուններ (որոնք, ի միջայլոց, ավելի հասանելի են մյուսներից). բազմանիստի յուրաքանչյուր n-անկյուն նիստը ունի n հատ ներքին հարթ անկյուն: Այդ անկյունները ուղղակի կանվանենք բազմանիստի հարթ անկյուններ և կփորձենք գտնել բազմանիստի բոլոր հարթ անկյունների գումարը, որը կնշանակենք՝
Պարզվում է որ այդ գումարներից ոչ մեկը անկախ չէ քառանիստի ձևից (տես օրինակ 15-ը): Ի՜նչ հիասթափություն: Չէինք սպասում, որ քառանիստը իրեն այդպես վատ կպահեր. կարծում էինք, թե այն նման է եռանկյանը: Սակայն, հավանաբար, ամեն ինչ դեռ կորած չէ, քանի որ դեռ բոլոր հնարավորությունները չեն սպառվել: Բազմանիստը, բացի դիտարկվածներից, ունի նաև այլ տեսակի անկյուններ (որոնք, ի միջայլոց, ավելի հասանելի են մյուսներից). բազմանիստի յուրաքանչյուր n-անկյուն նիստը ունի n հատ ներքին հարթ անկյուն: Այդ անկյունները ուղղակի կանվանենք բազմանիստի հարթ անկյուններ և կփորձենք գտնել բազմանիստի բոլոր հարթ անկյունների գումարը, որը կնշանակենք՝ 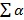 (տես նկարը):
(տես նկարը):
3°. Դիտարկում ենք: Եթե խնդրի լուծման համար հեռանկարային թվացող ոչ մի մոտեցում չի երևում, խնդրին մոտենանք որպես փորձարար՝ մի քանի բազմանիստների համար հաշվենք 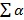 մեծությունը (հարթ անկյունների գումարը): Կարող ենք խորանարդից սկսել: Խորանարդի յուրաքանչյուր նիստ քառակուսի է, իսկ քառակուսու անկյունների գումարը 2
մեծությունը (հարթ անկյունների գումարը): Կարող ենք խորանարդից սկսել: Խորանարդի յուրաքանչյուր նիստ քառակուսի է, իսկ քառակուսու անկյունների գումարը 2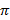 է:
է:
Քանի որ խորանարդը վեց նիստ ունի, հարթ անկյունների 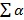 գումարը այս դեպքում կլինի
գումարը այս դեպքում կլինի 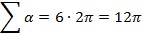
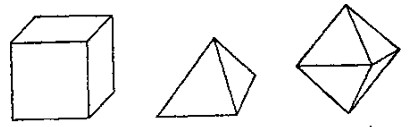 Ճիշտ նույն ձևով խնդիրը կարելի լուծել քառանիստի և ութանիստի դեպքում. այստեղ դժվարություն չի առաջանում:
Ճիշտ նույն ձևով խնդիրը կարելի լուծել քառանիստի և ութանիստի դեպքում. այստեղ դժվարություն չի առաջանում:
 Մինչև հիմա դիտարկված երեք բազմանիստներն էլ կանոնավոր էին: Բազմազանության համար ուսումնասիրենք ոչ կանոնավոր որևէ բազմանիստ, օրինակ հնգանկյուն պրիզմա (հնգանկյուն հիմքով պրիզմա):
Մինչև հիմա դիտարկված երեք բազմանիստներն էլ կանոնավոր էին: Բազմազանության համար ուսումնասիրենք ոչ կանոնավոր որևէ բազմանիստ, օրինակ հնգանկյուն պրիզմա (հնգանկյուն հիմքով պրիզմա):
Այն երկու տեսակի նիստեր ունի՝ հինգ հատ ուղղանկյուն և երկու հնգանկյուն, այդ պատճառով էլ այս դեպքում 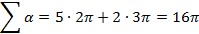 :
:
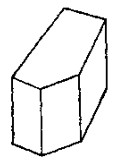
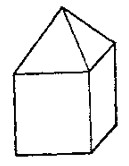 Այնուհետև դիտարկենք բազմանիստ, որը հազվադեպ կհանդիպեք դասարանում՝ բուրգով պսակված խորանարդ (բուրգաձև տանիքով, տես նկարը). նման «աշտարակը» ինը նիստ ունի, որոնցից հինգը քառակուսի են, իսկ չորսը՝ եռանկյուն. նրա հարթ անկյունների գումարը կլինի
Այնուհետև դիտարկենք բազմանիստ, որը հազվադեպ կհանդիպեք դասարանում՝ բուրգով պսակված խորանարդ (բուրգաձև տանիքով, տես նկարը). նման «աշտարակը» ինը նիստ ունի, որոնցից հինգը քառակուսի են, իսկ չորսը՝ եռանկյուն. նրա հարթ անկյունների գումարը կլինի 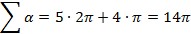 :
:
Մեր դիտարկումների արդյունքները ամփոփված են աղյուսակում. դիտարկված բազմանիստերը հեշտությամբ ճանաչելու համար յուրաքանչյուրի նիստերի քանակն է գրված՝ Ն.
|
Բազմանիստի տեսակը |
Ն |
|
|
Խորանարդ |
6 |
12 |
|
Քառանիստ |
4 |
4 |
|
Ութանիստ |
8 |
8 |
|
Հնգանյուն պրիզմա |
7 |
16 |
|
Աշտարակ |
9 |
14 |
Նկատո՞ւմ եք ուշադրության արժանի ինչ-որ բան՝ որևէ օրինաչափություն կամ կանոնավորություն:
4°. Դիտարկում ենք՝ ղեկավարվելով որոշակի գաղափարով: Զարմանալի չէ, որ առայժմ ոչ մի արժեքավոր բան չենք հայտնաբերել մեր հավաքած արդյունքներում. առանց որոշակի գաղափարի իրականացվող մաքուր դիտարկումը հազվադեպ է բերում ուշադրության արժանի արդյունքի:
Մեր գործողությունների մասին մի քիչ մտորելով, կարող ենք փակուղուց ելք գտնել: 3° կետում հաճախ հաշվում էինք հարթ անկյունների 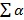 գումարը, նախօրոք հաշվելով նույն նիստին պատկանող անկյունների գումարը. այս վերջին գումարը ճշգրիտ գիտենք, և, ըստ էության, հենց դա էլ մեր հետազոտության ելակետն է: Բազմազանության համար հիմա դիտարկենք բազմանիստի մի գագաթի մոտ գտնվող հարթ անկյունների գումարը: Այդ գումարը ճշգրիտ չգիտենք, բայց այն պետք է փոքր լինի 2
գումարը, նախօրոք հաշվելով նույն նիստին պատկանող անկյունների գումարը. այս վերջին գումարը ճշգրիտ գիտենք, և, ըստ էության, հենց դա էլ մեր հետազոտության ելակետն է: Բազմազանության համար հիմա դիտարկենք բազմանիստի մի գագաթի մոտ գտնվող հարթ անկյունների գումարը: Այդ գումարը ճշգրիտ չգիտենք, բայց այն պետք է փոքր լինի 2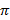 –ից, քանի որ 2
–ից, քանի որ 2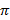 –ն լրիվ անկյան չափն է: (Իհարկե, այստեղ կսահմանափակվենք ուռուցիկ բազմանիստներով. փաստը, որը հիշատակում ենք, ինտուիտիվորեն պարզ է, խիստ ապացույցը կարելի գտնել Էվկլիդեսի մոտ, տես XI, 21[1]): Գ-ով նշանակենք դիտարկվող բազմանիստի գագաթների քանակը, այդ դեպքում հարթ անկյունների ընդհանուր գումարի համար
–ն լրիվ անկյան չափն է: (Իհարկե, այստեղ կսահմանափակվենք ուռուցիկ բազմանիստներով. փաստը, որը հիշատակում ենք, ինտուիտիվորեն պարզ է, խիստ ապացույցը կարելի գտնել Էվկլիդեսի մոտ, տես XI, 21[1]): Գ-ով նշանակենք դիտարկվող բազմանիստի գագաթների քանակը, այդ դեպքում հարթ անկյունների ընդհանուր գումարի համար 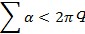 ։
։
Այս առնչությունը ստուգենք «փորձնական» նյութի համար: Ընդարձակնեք մեր կազմած աղյուսակը:
|
Բազմանիստի տեսակը |
Ն |
|
Գ |
2 |
|
Խորանարդ |
6 |
12 |
8 |
16 |
|
Քառանիստ |
4 |
4 |
4 |
8 |
|
Ութանիստ |
8 |
8 |
6 |
12 |
|
Հնգանկյուն պրիզմա |
7 |
16 |
10 |
20 |
|
Աշտարակ |
9 |
14 |
9 |
18 |
Այս աղյուսակից երևում է, որ բոլոր բազմանիստերի համար 2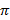 Գ-ն ավելի մեծ է
Գ-ն ավելի մեծ է 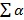 -ից. աղյուսակը ուշադիր զննելու դեպքում կնկատենք, որ այդ թվերի տարբերությոնը հաստատուն է՝
-ից. աղյուսակը ուշադիր զննելու դեպքում կնկատենք, որ այդ թվերի տարբերությոնը հաստատուն է՝ 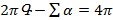 :
:
Հազիվ թե ցանկալի է մտածելը, որ նկատված կախվածությունը ճիշտ է ոչ միայն ուսումնասիրված դեպքերում, այլև բոլոր ուռուցիկ բազմանիստների համար:
Այսպիսով հանգում ենք եզրակացության, որ 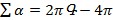 (*)։
(*)։
Փակագծում նշանը, որով նշված է գրված առնչությունը, մեզ պետք է հիշեցնի, որ այն դեռ ապացուցված չէ, վարկած է, ոչ թե թեորեմ:
5°. Ստուգենք մեր վարկածը: Հաջող գաղափարով ուղղորդված մեր դիտարկումը հիանալի ենթադրություն անել թույլ տվեց, բայց արդյո՞ք չենք սխալվում: Այդ ենթադրությունը մի քանի օրինակներով էլ ստուգենք: Բացի խորանարդից, քառանիստից, ութանիստից, որոնց արդեն հանդիպել ենք, երկու կանոնավոր բազմանիստ էլ կա՝ տասներկուանիստը (Ն=12) և քսանանիստը (Ն=20) և պետք է դրանք էլ դիտարկել: Ընթերցողն ինքը հեշտությամբ կարող է շարունակել աղյուսակը՝ ընդգրկելով նշված մարմինները:
|
Բազմանիստի տեսակը |
Ն |
|
Գ |
2 |
|
տասներկուանիստ |
12 |
36 |
20 |
40 |
|
քսանանիստ |
20 |
20 |
12 |
24 |
|
n-անկյուն պրիզմա |
n+2 |
(4n-4) |
2n |
4 |
|
Հնգանկյուն պրիզմա |
7 |
16 |
10 |
20 |
|
Աշտարակ |
9 |
14 |
9 |
18 |
Ուռա, ենթադրված առնչությունը տեղի ունի բոլոր դիտարկված դեպքերի համար: Սակայն վերջին հանգամանքը միայն չի ժխտում ենթադրյալ թեորեմը, բայց չի ապացուցում այն:
6°. Որոշ մտորումներ հետագա անելիքների մասին: 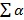 հաշվելիս մենք մի քանի անգամ օգտվեցինք նույն հնարքից՝ միշտ սկսում ենք նույն նիստին պատկանող անկյունների գումարը հաշվելուց: Ինչո՞ւ այս ընթացակարգը չկիրառենք ընդհանուր դեպքում: Այս ծրագիրը իրագործելու համար հարկ կլինի նոր նշանակումներ ներմուծել: Դիցուք, S1, S2, S3, ..., SՆ համապատասխանաբար նշանակում են առաջին, երկրորդ, երրորդ, ..., վերջին նիստին պատկանող կողերի քանակը: Այս նշանակումներով`
հաշվելիս մենք մի քանի անգամ օգտվեցինք նույն հնարքից՝ միշտ սկսում ենք նույն նիստին պատկանող անկյունների գումարը հաշվելուց: Ինչո՞ւ այս ընթացակարգը չկիրառենք ընդհանուր դեպքում: Այս ծրագիրը իրագործելու համար հարկ կլինի նոր նշանակումներ ներմուծել: Դիցուք, S1, S2, S3, ..., SՆ համապատասխանաբար նշանակում են առաջին, երկրորդ, երրորդ, ..., վերջին նիստին պատկանող կողերի քանակը: Այս նշանակումներով`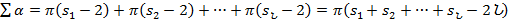 :
:
Այնուհետև, բոլոր Ն նիստերի կողերի ընդհանուր թիվը կլինի S1+S2+S3+...+SՆ: Այս գումարում բազմանիստի յուրաքանչյուր կողը ճիշտ երկու անգամ է հաշվված (քանի որ նրանով հատվում են երկու նիստեր) և այդ պատճառով S1+S2+S3+...+SՆ=2Կ, որտեղ Կ-ով նշանակված է բազմանիստի կողերի քանակը: Այստեղից ստանում ենք 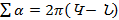 (!)։
(!)։
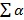 -ի համար գտանք երկրորդ արտահայտությունը, բայց նրանց միջև էական տարբերություն կա. առաջին բանաձևի ճշմարտացիությունը մենք միայն ենթադրել ենք, մինչդեռ (!) բանաձևինը ապացուցել ենք: Այդ երկու բանաձևերից արտաքսելով
-ի համար գտանք երկրորդ արտահայտությունը, բայց նրանց միջև էական տարբերություն կա. առաջին բանաձևի ճշմարտացիությունը մենք միայն ենթադրել ենք, մինչդեռ (!) բանաձևինը ապացուցել ենք: Այդ երկու բանաձևերից արտաքսելով 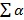 –ն՝ կստանանք Ն+Գ=Կ+2(??), որը դեռևս ապացուցված չէ և այդ պատճառով նշված է (??) նշանով:
–ն՝ կստանանք Ն+Գ=Կ+2(??), որը դեռևս ապացուցված չէ և այդ պատճառով նշված է (??) նշանով:
Ըստ էության (??) բանաձևը նույնքան կասկածելի է, որքան (?) արտահայտությունը. հաշվի առնելով այս բանաձևերի կապը ապացուցված (!) բանաձևի հետ, նրանցից մեկը կարելի արտածել մյուսից, և այդ պատճառով կա՛մ նրանք երկուսն էլ ճիշտ են, կա՛մ երկուսն էլ ճիշտ չեն. այդ երկու արտահայտությունները համարժեք են:
7°. Ստուգում: Քաջ հայտնի (??) առնչությունը, ինչպես նաև պակաս հայտնի (?) առնչությունը, գտել է Էյլերը, ով չգիտեր, որ իրենից առաջ նույն առնչություններին հանգել էր Դեկարտը: Այս հարցի վերաբերյալ Դեկարտի աշխատանքի մասին գիտենք մի քանի կարճ արտահատությունների շնորհիվ, որոնք գտնվել են նրա չհրապարակված ձեռագրերում և հրապարակվել են Էյլերի մահից հարյուր տարի հետո: Էյլերը այս հարցին երկու հատուկ հոդված է հատկացրել և մեկում էլ կարճ անդրադարձել է: Վերջին ծանոթությունը վերաբերում է քառանիստի մարմնային անկյունների գումարին (որը, ինչպես արդեն հիշատակել ենք 20 կետում, կախված է նրա ձևից):
Նախորդ կետերում այդ հարցը քննարկելիս հետևել ենք Էյլերի առաջին հոդվածին, որտեղ նա պատմում է այն մասին, թե իրեն ինչպես է հաջողվել անել իր բացահայտումը, սակայն ձևական ապացույց չի տալիս՝ սահմանափակվելով բազմաթիվ ստուգումներով: Այս հարցում կհետևենք Էյլերին: Միավորելով նախորդ աղյուսակների տվյալները և ընդգրկելով Կ մեծությունը, կստանանք
|
Բազմանիստը |
Ն |
Գ |
Կ |
|
Քառանիստ |
4 |
4 |
6 |
|
Խորանարդ |
6 |
8 |
12 |
|
Ութանիստ |
8 |
6 |
12 |
|
Տասներկուանիստ |
12 |
20 |
30 |
|
Քսանանիստ |
20 |
12 |
30 |
|
Աշտարակ |
9 |
9 |
16 |
|
n-անկյուն պրիզմա |
n+2 |
2n |
3n |
|
n-անկյուն բուրգ |
n+1 |
n+1 |
2n |
|
n-անկյուն կրկնաբուրգ |
2n |
n+2 |
3n |
Ենթադրվող (??) առնչությունը հաստատվում է աղյուսակի յուրաքանչյուր տողով, ինչը այն դարձնում է շատ համոզիչ, բայց, իհարկե, հավասարազոր չէ ապացույցի:
8°. Քննում ենք ստացված արդյունքները: Էյլերն իր երկրորդ հոդվածում փորձեց ապացուցել (??) առնչությունը, սակայն հաջողություն չունեցավ: Եվ այնուամենայնիվ, նախորդ դատողություններն ըստ էության մեզ ընդհուպ մոտեցրեցին ապացույցին. միայն պետք է հստակորեն պատկերացնել, թե որքան հեռու է մեզ հաջողվել առաջ գնալ: Փորձենք ինչպես հարկն է պարզել, թե ինչ է նշանակում (!) արդյունքը: Հատկապես ուշադրություն դարձնենք, թե ինչ է ստացվում, երբ բազմանիստը փոխում է իր ձևը: Այդ փոփոխությունը կհամարենք անընդհատ, այսինքն կենթադրենք, որ նիստերի թեքվածությունը աստիճանաբար է կատարվում, ենթադրելով, որ նիստերի հատման գծերի և կետերի (բասմանիստի կողերը և գագաթները) նրա առաջացրած մշտական փոփոխությունը չի բերում բազմանիստի «ընդհանուր տեսքի» կամ «ձևաբանական կառուցվածքի» փոփոխության, այլ կերպ ասած, անփոփոխ է թողնում նրա կողերի և գագաթների միջև կախվածությունը: Այս ենթադրությունների դեպքում Ն, Կ և Գ թվերը (այսինքն՝ համապատասխանաբար նիստերի, կողերի և գագաթների քանակը) նույնպես անփոփոխ են մնում: Բազմանիստի այսպիսի ձևափոխությունը կարող է փոփոխել առանձին վերցրած յուրաքանչյուր 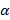 հարթ անկյունը. սակայն (!) առնչության շնորհիվ (իսկ մենք ապացուցեցինք) այն չի կարող ազդել հարթ անկյունների միագումարության վրա, այսինքն բոլոր հարթ անկյունների
հարթ անկյունը. սակայն (!) առնչության շնորհիվ (իսկ մենք ապացուցեցինք) այն չի կարող ազդել հարթ անկյունների միագումարության վրա, այսինքն բոլոր հարթ անկյունների  գումարը թողնում է անփոփոխ: Այս հանգամանքը թույլատրում է նկատել այն հնարավորությունները, որոնք մեր առջև բացում է բազմանիստի սկզբնական ձևի այդպիսի ձևափոխությունը. վերջինիս պետք է առավել հարմար ձև տալ, ինչը կհեշտացնի
գումարը թողնում է անփոփոխ: Այս հանգամանքը թույլատրում է նկատել այն հնարավորությունները, որոնք մեր առջև բացում է բազմանիստի սկզբնական ձևի այդպիսի ձևափոխությունը. վերջինիս պետք է առավել հարմար ձև տալ, ինչը կհեշտացնի  գումարը (անփոփոխ մնացող) հաշվելը:
գումարը (անփոփոխ մնացող) հաշվելը:
 Իսկապես, բազմանիստի նիստերից մեկը որպես հիմք ընդունենք: Ընտրած հիմքը տեղադրենք հորիզոնական և այն «ձգենք» (միաժամանակ «սեղմելով» մյուս նիստերը) այնպես, որ նրա վրա հնարավոր լինի ուղղանկյունաձև պրոյեկտել ամբողջ բազմանիստը:
Իսկապես, բազմանիստի նիստերից մեկը որպես հիմք ընդունենք: Ընտրած հիմքը տեղադրենք հորիզոնական և այն «ձգենք» (միաժամանակ «սեղմելով» մյուս նիստերը) այնպես, որ նրա վրա հնարավոր լինի ուղղանկյունաձև պրոյեկտել ամբողջ բազմանիստը:
Նկարներից առաջինում պատկերված է, թե ինչ կստացվի խորանարդի դեպքում, իսկ երկրորդում՝ ընդհանուր տեսքի բազմանիստի դեպքը:
Երկու դեպքում էլ մեր առջև տափակացված բազմանիստ է, իրար վրա դրված երկու բազմանկյուն թիթեղների (ընդհանուր ուրվագծով) միաձուլում, որոնցից վերևինը տրոհված է Ն-1 բազմանկյունների (որտեղ Ն-ը սկզբնական բազմանիստի նիստերի քանակն է), ներքևինը (ձգված հիմքը) ավելի փոքր մասերի չի տրոհվում: Արտաքին «եզրապատող» բազմանկյան կողմերի քանակը նշանակենք r:
Հաշվենք 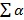 գումարը տափակեցված բազմանիստի համար (գիտենք, որ այն մնում է նույնը, ինչ սկզբնական բազմանիստի համար): Այս գումարը երեք մասից է կազմված. ստորին թիթեղի («ձգված» հիմքի) անկյունների գումարը կլինի (r-2)
գումարը տափակեցված բազմանիստի համար (գիտենք, որ այն մնում է նույնը, ինչ սկզբնական բազմանիստի համար): Այս գումարը երեք մասից է կազմված. ստորին թիթեղի («ձգված» հիմքի) անկյունների գումարը կլինի (r-2)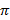 , վերին թիթեղի ուրվագիծը հանդիսացող «եզրափակող» բազմանկյան անկյունների գումարը, որը նույն արժեքն ունի. վերին թիթեղի բոլոր ներքին անկյունների գումարը՝ այդ բոլոր անկյունները խմբավորվում են Գ-r ներքին գագաթների շուրջը և նրանց գումարը հավասար է (Գ-r)2
, վերին թիթեղի ուրվագիծը հանդիսացող «եզրափակող» բազմանկյան անկյունների գումարը, որը նույն արժեքն ունի. վերին թիթեղի բոլոր ներքին անկյունների գումարը՝ այդ բոլոր անկյունները խմբավորվում են Գ-r ներքին գագաթների շուրջը և նրանց գումարը հավասար է (Գ-r)2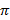 :
:
Հաշվելով մեր երեք բաղադրիչների գումարը, կստանանք 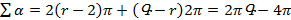 :
:
Սա ապացուցում է մեր (?) ենթադրությունը, և, հետևաբար՝ (??) ենթադրությունը:
§7. Գիտական մեթոդ. կռահեք և փորձեք
Նախորդ օրինակները մի քանի ընդհանուր նկատառումներ անելու հնարավորություն են տալիս: Իհարկե, այդ նկատառումները ավելի բնականորեն կառաջանային և ավելի փաստարկված կլինեին, եթե մեր օրինակները ավելի մանրամասնորեն քննարկեինք և դրանց թիվը ավելի շատ լիներ (նայիր այս գլխի վերջում բերված վարժությունները և լրացուցիչ դիտարկումները): Սակայն նույնիսկ արդեն դիտարկվածի հիմքի վրա կարելի է ինչ-որ բան ասել5
Դիտարկելը կարող է բացահայտման հանգեցնել:
Դիտարկումը ինչ-որ պարբերաբար կրկնվող փաստ, սխեմա կամ օրենք հայտնագործելու նպատակ ունի:
Դիտարկումը ավելի մեծ հավանականություն ունի ուշադրության արժանի արդյունքի հասցնելու, եթե այն ուղղորդվում է ինչ-որ հաջող գաղափարով կամ մտքով:
Դիտարկումը կարող է ընդհանրացումների և ենթադրությունների համար հիմք լինել, բայց այն ապացույց չէ:
Ստուգեք ձեր ենթադրությունը մասնավոր դեպքերի և այն փաստերի դեպքում, որոնք դրանից հետևում են:
Յուրաքանչյուր հաստատված մասնավոր դեպք կամ ճշմարիտ հետևություն հիմնավոր է դարձնում ձեր ենթադրությունը:
Մանրազնին տարբերեք ապացույցի մասին ակնարկը բուն ապացույցից, ենթադրությունը՝ փաստից:
Մի՛ անտեսեք նմանությունները. նրանք կարող են հանգեցնել նոր փաստեր բացահայտելուն (դա ցույց տվեցինք բազմանկյունների և բազմանիստերի միջև նմանակումից. տես 6-րդ պարագրաֆի 1°):
Ուսումնասիրեք սահմանային դեպքերը (այլափոխված եռանկյունների և բազմանիստերի նման. տես պարագրաֆ 4-ը և 6-րդ պարագրաֆի 8°):
Արված դիտողություններն արժանի են ավելի ճշգրիտ, ավելի մանրակրկիտ և ավելի համակարգված ձևակերպման և ավելի շատ ցուցադրական նյութի:
Սակայն նույնիսկ այն տեսքով, ինչպիսին նրանք տրված են այս գրքում և ինչպիսին կարող են առաջանալ վերևում բերվածներին նման օրինակներից կամ դասարանում լավ կազմակերպված քննարկումից, նրանք կարող են միջնակարգ դպրոցի սովորողի մոտ (կամ այլ աստիճանի սովորողի) ստեղծել բավականաչափ հստակ պատկերացում գիտական հետազոտության բնույթի մասին: Փիլիսոփաները, ինչպես առաջ, այնպես էլ հիմա, տարբեր հայացքներ են արտահայտել և արտահայտում այնպիսի հասկացությունների բովանդակության մասին, ինչպես. «գիտական հետազոտություն», «գիտական մեթոդ», «ինդուկցիա» և այլն: Բայց ինչո՞վ են նրանք զբաղվում: Նրանք վարկածներ են մտածում, իսկ հետո դրանք փորձով ստուգում են: Եթե ցանկանում եք գիտական մեթոդի բնութագրումը ունենալ երեք բառով, իմ կարծիքով, սա է՝ Կռահեք և փորձեք:
§8. «Գիտա-հետազոտական» բնույթի խնդիրների մի քանի բնորոշ գծերի մասին
Այստեղ մեր դիտարկած խնդիրները ինչ-որ չափով տարբերվում են սովորական, ամենօրյա խնդիրներից: Այստեղ ցանկանում եմ երեք տարբերություն նշել:
1°. Դպրոցականն իր խնդիրն ստանում է պատրաստի տեսքով՝ ուսուցչից կամ դասագրքից, և հաճախ ուսուցիչը չի էլ հոգում, որ այդ խնդիրը հետաքրքրի աշակերտին (դասագրքի դեպքում կարելի է ավելի մեծ վստահութկամբ պնդել): Այնինչ մաթեմատիկայում խնդրի ընտրությունը գուցե ամենակարևոր քայլն է. նա պետք հորինի, պետք է գտնի այն խնդիրը, որն իրեն կգրավի և արժանի կլինի նրա ջանքերին, բայց, միևնույն ժամանակ, նրա ուժերից վեր չպետք է լինի: 2-րդ և 4-րդ պարագրաֆներում ուսուցիչն այնպես է անում, ուր սովորողը կարողանա մասնակցել խնդիր ձևակերպելուն (համեմատիր 5-րդ պարագրաֆի 1° կետը և 14-րդ գլուխը):
2°. Խնդրագրքերի և դասագրքերի խնդիրների մեծ մասը քիչ կապ ունեն իրար հետ. նրանք ծառայում մի որոշակի կանոն ցուցադրելու համար և թույլ են տալիս միայն այն կիրառելու փորձառություն ձեռք բերել: Երբ այս խնդիրներն իրենց ծառայությունը մատուցում են, նրանց կարելի է (և պետք է) մոռանալ: Ի հակադրություն դրանց՝ 2-րդ և 6-րդ պարագրաֆների խնդիրները խորը բովանդակությամբ խնդիրներ են. նրանք ուսանելի հարցեր են ծնում, որոնցից էլ իրենց հերթին նոր հետաքրքիր խնդիրներ են առաջանում, և այդպես շարունակվում է այնքան ժամանակ, մինչև սկզբնական խնդրի ճյուղավորումները ծածկում են բավականին լայն տիրույթ: (Նման ճյուղավորումներ մանրամասնորեն կդիտարկվեն այս գլխի վերջի վարժություններում և լրացուցիչ դիտողություններում):
3°. Դպրոցներից շատերում «կռահելու» վրա արգելք է դրված, մինչդեռ ցանկացած գիտական հետազոտությունում (այդ թվում և մաթեմատիկայում) գրեթե կանոն է՝ «սկզբում կռահիր և հետո ապացուցիր»: Մեր դիտարկած խնդիրներում դիտարկումները, ենթադրությունները, ինդուկտիվ մտահանգումները, կարճ ասած՝ ճշմարտանման դատողությունները բացառիկ դեր են խաղում:
4°. Չնայած 1° կետը (մասնակցություն խնդիրը կազմելուն) ամենևին էլ երկրորդական չէ, հաջորդ երկու կետերն առավել կարևոր են: Խորը ենթատեքստով խնդիրները, որոնք կապված են մեզ շրջապատող իրականությանը կամ մտածողության այլ բնագավառներին, ինչպես նաև ճշմարտանման դատողություններ օգտագործելուն միտված խնդիրները, որոնք սովորողի մոտ զարգացնում են մտածելու կարողությունը, կարող են ավելի շուտ նպաստել մտավոր հասունացմանը, քան այն խնդիրները, որոնցով լցված են դպրոցական դասագրքերը, և որոնք պիտանի են միայն մի առանձին օրենքի կիրառության գործում ձեռքը վարժեցնելուն:
§9. Եզրակացություններ
Այս գլխի վերջում բերվածների նման օրինակները և դիտողությունները կարելի է, իմ կարծիքով, ուսումնասիրել միջնակարգ դպրոցում, և դրանք սովորողներին օգտակար կլինեն երեք նկատառումներով։
Առաջինը՝ դրանք կարող են մաթեմատիկայի նկատմամբ ճաշակ ներարկել, քանի որ ինքնուրույն, ստեղծագործ աշխատանքի հնարավորություն են տալիս.
երկրորդ (և սա ավելի կարևոր է, քանի որ մեծ քանակով աշակերտների շահեր է շոշափում)՝ դրանք օգնում են հասկանալու ոչ միայն մաթեմատիկան, այլև ուրիշ գիտություններ. նրանք սկզբնական, բայց լրիվ բավարար հասկացություն են տալիս «ինդուկտիվ հետազոտության» և «գիտական մեթոդի» մասին.
Երրորդ՝ նրանք սովորողների համար բացահայտում են մաթեմատիկայի մի կարևոր կողմ, որը որքան կարևոր է, նույնքան և սակավ է հիշատակվում. այս խնդիրներում մաթեմատիկան երևում է որպես գիտություն, որը սերտորեն կապված է ուրիշ բնական գիտությունների հետ, «փորձարարական գիտության» տարատեսակ, որում դիտարկումը (փորձը) և համեմատումը կարող են հասցնել բացահայտումների (մաթեմատիկայի այս կողմը հատկապես պետք է հետաքրքրի մաթեմատիկայի ապագա «կիրառողներին»՝ բնախույզներին և ճարտարագետներին):
Հուսով եմ, որ մաթեմատիկական բացահայտումը, գիտական մեթոդը և ինդուկցիան, որպես մաթեմատիկական տեսակետներ, ապագայի միջնակարգ դպրոցներում այդպես արհամարհված չեն լինի, ինչպես այսօր:
Թարգմանություն ռուսերենից
Լուսանկարի աղբյուրը
[1]Այս առաջադրումն ապացուցվում է տարածաչափության բոլոր դասագրքերում:
- Բացվել է 2382 անգամ

