Մտքի կարգապահություն

Մաթեմատիկական հայտնություն

11-րդ գլուխը

Գլուխ 12

Մեթոդը այն բանի դասավորելն ու կարգավորելն է, ինչին պետք է ուղղված լինի մտքի սուր ծայրը՝ ինչ-որ նոր ճշմարտություն հայտնաբերելու նպատակով:
Դեկարտ, Միտքը ղեկավարելու կանոններ, V կանոն, Ընտիր երկեր, էջ 95

§ 1. Ինչպես է պետք մտածել

11-րդ գլխում փորձ էր արված նկարագրելու խնդիր լուծողի (մաթեմատիկական կամ ոչ մաթեմատիկական) մտավոր գործունեության բնորոշ առանձնահատկությունները: Բայց արդյո՞ք բնորոշը նաև բանականն է: Մեր մտավոր գործողությունը կարող է այդպես ընթանալ, բայց պարտադիր է, որ հենց այդպե՞ս ընթանա:

Այս հարցերին, իրենց անորոշ ընդհանրության պատճառով, բավականին դժվար է միանշանակ պատասխանելը, սակայն այս գլխի հիմնական գաղափարամիտությունը ցույց տալու համար դրանք մեզ պետք են: Ղեկավարվելով խնդիր լուծողի մտավոր աշխատանքի փորձով, որին ծանոթացանք գլուխ 11-ում, փորձենք թվարկել մտավոր գործողությունները (քայլեր, ընթացակարգեր և այլն), որոնք սովորաբար օգտակար են լինում խնդիր լուծելիս. Այդ ընթացքում կձգտենք ցույց տալ յուրաքանչյուր այդպիսի գործողության տեղը խնդիր լուծելու պրոցեսում:

Մենք այս, որպես կանոն, խնդիր լուծելու համար կիրառվող օգտակար գործողությունները, կներկայացնենք հակիրճ, խտացված տեսքով, դրա համար օգտագործելով «ստանդարտ» հարցեր և հանձնարարականներ: Ընթերցողի համար պետք է պարզ լինի, որ նման հարցերը և հանձնարարականները կարելի է մեկնաբանել երկու ձևով՝ կա՛մ որպես խնդիր լուծողի ինքն իր հետ զրույցից հատվածներ, կա՛մ ավելի փորձառու ուսուցչի խոսքը սովորողին, որին ցանկանում է օգնել:

§ 2. Ուշադրության կենտրոնացում նպատակի վրա

Երբ պետք է խնդիր լուծեք, դրա մասին հաճախ եք հիշում, նույնիսկ այնքան հաճախ, որ այն դառնում է սևեռուն գաղափար: Սակայն դուք ոչ թե պետք է ուղղակի մտածեք խնդրի մասին, մտածեք մի տեսակ, այսպես ասած, անորոշ կերպով, այլ պետք է մշտապես ուղղված լինեք խնդրին, բացահայտորեն տեսնեք այն և ամենից առաջ ինքներդ ձեզ կարևոր հարցը տաք՝ ի՞նչ է պահանջվում:

Խնդիրը լուծելու ընթացքում այս հարցը տալու շատ հարմար առիթներ կլինեն: Երբ չափից ավելի խորացել եք կողմնակի ճանապարհով, որը կարող է վերջում փակուղային լինել կամ նպատակից շատ հեռացնել, երբ ձեր միտքը սկսում է թափառել, շատ կարևոր է նորից հարցնելը՝ ի՞նչ է պահանջվում,- և դրանով նպատակը նորից բերել ուշադրության կենտրոն:

Որոշման խնդրի նպատակը անհայտն է: Ուշադրությունն այդ նպատակի վրա կենտրոնացնելու համար ինքներդ ձեզ հարցրեք՝ ի՞նչն է անհայտ: Ապացուցման խնդրի նպատակը եզրակացությունն է, հետևությունը. այս դեպքում համապատասխան հարցը այս տեսքը կունենա՝ ո՞րն է եզրակցությունը:

Երբ արդեն պարզորոշ տարբերում եք խնդրի նպատակը, այսինքն՝ որոնելի օբյեկտը, անհրաժեշտ է անցնել գույքագրելուն այն ամենը, ինչ ունեք ձեր տրամադրության տակ, որպեսզի առանձնացնեք այն օբյեկտները, որոնք որոշակի հավանականությամբ կարող են օգտագործվել նպատակին հասնելու համար. ձեզ պետք է հարցնեք՝ ի՞նչ ունենք:

Ենթադրենք՝ ցանկանում եք կապ հաստատել երկու տարրերի միջև, ճանապարհ բացել մի տարրից մինչև մյուսը. այստեղ կարող է ձեզ օգնել այդ տարրերը հերթականությամբ դիտարկելը՝ սկսում եք դրանցից մեկից, հետո անցնում եք մյուսին, այնպես որ հնարավորություն եք ունենում վերևում նշված հարցերը հաջորդաբար տալու. ի՞նչ է պահանջվում. ի՞նչ ունեցանք:

Որոշման խնդիրների դեպքում այդ հարցերը այսպիսին են՝ ո՞րն է անհայտը. ի՞նչ է տրված. ո՞րն է պայմանը: Ապացուցման խնդիրների դեպքում դրանք այսպիսին են՝ ո՞րն է եզրակացությունը. ի՞նչն է պայմանը (նախադրյալը):

Ինչո՞ւ են այս հարցերն այդքան կարևոր: Որովհետև նրանք ստիպում են ուշադրություն դարձնել խնդրի նշված տարրերին: Ըստ Դեկարտի (տես այս գլխի բնաբանը) խնդիրը լուծելու մեթոդն այն է, որ ուշադրություն դարձնեք հարցին վերաբերող բոլոր տարրերին՝ մեկը մյուսի ետևից, հարկ եղած հաջորդականությամբ: Քիչ ենք կասկածում, որ որոշման խնդրի գլխավոր մասերը (անհայտը, տվյալը և պայմանը) և ապացուցման խնդրի գլխավոր մասերը (եզրակացությունը և պայմանը) խնդրին վերաբերող տարրերն են: Երբեմն դրանք այնքան կարևոր են լինում, որ անհրաժեշտ է թվում դրանք ուսումնասիրել հնարավորին չափ շուտ. խնդիրը լավ հասկանալուց հետո ձեր ուշադրությունը դարձրեք նրա գլխավոր մասերին:

§ 3. Ակնկալիքների գնահատումը

Իր խնդրի լուծումով լրջորեն զբաղված մարդը զգում է նպատակի մոտիկությունը և դրան գնալու իր արագությունը. նաև զգում է ցանկացած փոփոխություն, որը ազդում է իր ծրագրի հեռանկարի վրա: Բայց երբեմն ցանկալի է լինում միայն զգացողություններից մի քիչ հեռանալը, խնդիրը լուծելու սեփական հնարավորությունները ավելի սթափ գնահատելը, խնդիրը «ախտորոշելը», ակնկալիքները գնահատելը. հենց այսպիսին են ներքևում բերված հարցերի միտումները:

Որոշ խնդիրներ անհույս են լինում: Եթե խնդիրն անհույս է, չարժե շատ խորանալ. և այստեղ հարցնում ենք՝ իսկ ընդհանրապես այս հարցի պատասխանը կա՞. կա՞ հստակ, խելամիտ պատասխան. եթե պատասխան կա, կկարողանա՞մ գտնել:

Եթե որոնման խնդրի հետ գործ ունենք, պետք է հարցնենք՝ գոյություն ունի՞ լուծում։ Կարելի է և ավելի տարբերակված հարցեր տալ՝ արդյո՞ք միակ լուծում գոյություն ունի, թե՞ դրանք մի քանիսն են, կամ ընդհանրապես լուծում չունի. պայմանները միանգամայն բավարա՞ր են լուծումը գտնելու համար, թե՞ դրանք չափից շատ են կամ անբավարար են:

Երբ գործ ունենք ապացուցման խնդրի հետ, համապատասխան հարցերն են՝ թեորեմը ճշմարի՞տ է, սխա՞լ է: Կարելի է և ավելի տարբերակված հարցեր տալ՝ ճշմարի՞տ է արդյոք թեորեմը. թեորեմի ճշմարիտ լինելու համար պե՞տք է, որ պայմանը ավելի խիստ լինի0 թեորեմը ճի՞շտ է ձևակերպված. թեորեմի ճիշտ լինելու համար բավարար չէ՞ր ավելի թույլ պայման և այլն:

Իրականում հենց նոր ձևակերպված հարցերից ոչ մեկին չենք կարող որոշակիորեն պատասխանել, քանի չենք վերջացրել մեր աշխատանքը, այսինքն՝ չենք լուծել խնդիրը: Բայց այս հարցերն իրենց էությամբ չեն էլ ենթադրում հստակ պատասխաններ, նրանք նախատեսված են միայն մոտավոր պատասխանների, կռահումների համար: Ճիշտ կտահելու համար կարող ենք ճշգրտել մեր դիրքորոշումը դիտարկվող խնդրի նկատմամբ, և հենց դրան էլ ձգտում ենք: Բերված հարցերը ձևակերպված են համառոտ ոճով՝ սովորական զրույցի, խոսակցության համար: Հարցերի ավելի զգույշ (և ավելի ճշգրիտ) ձևակերպումները այսպիսին են՝ հավանականություն կա՞ (և ինչքա՞ն մեծ), որ խնդրի լուծում գոյություն ունի. ձևակերպված թեորեմը կարող է լինել և՛ ճիշտ, և՛ սխալ, ո՞րն է ավելի հավանական:

Ո՞ր պահին, որքա՞ն շուտ պետք է նման հարցեր տանք: Այս հարցին չկա (և չի կարող լինել, չպետք է լինի) ոչ մի կոշտ և հապճեպ պատասխան: Շատ հաճախ նրանք § 2-ում բերված հարցերի շարունակությունն են, որոնք վերաբերում էին խնդրի գլխավոր մասերին:

§ 4. Հածում. մոտեցման փնտրտուք

Վերջնական նպատակը հուշում է միջոցները. նպատակը ուսումնասիրելը (անհայտը, եզրակացությունը) կարող է օգնել գտնելու խնդրի լուծման մոտեցումը: Արդեն գիտեք, որ հարցը հարց է ծնում՝ ի՞նչ է պահանջվում. ի՞նչ է անհայտը. ինչպե՞ս կարելի է գտնել նման անհայտը. ի՞նչ տվյալներ են պետք նման անհայտը գտնելու համար: Հենց այսպիսի հարցերը կարող են ճանապարհի սկիզբ լինել, որը հենված է հակառակ ուղղությամբ շարժվելու վրա. օրինակ, եթե առաջադրված խնդրում կարողացել ենք տեսնել «տվյալները», որոնք հնարավորություն են տալիս անհայտը գտնելու, կարող ենք դրանք ընդունել որպես օժանդակ խնդրի «միջանկյալ» նպատակի դրվածքի համար պատասխանատու և սկսել վերջից դեպի սկիզբ շարժվելը:

Ապացուցման խնդիրներում համապատասխան հարցերը կլինեն՝ ի՞նչ է պահանջվում. ո՞րն է եզրակացությունը. ինչպե՞ս կարելի է նման եզրակացություն ստանալ. ո՞ր պայմանից կարելի է նման եզրակացություն ստանալ:

Անհայտի (կամ թեորեմի եզրակացության) վրա շեշտադրում անելու փոխարեն կարող ենք մեր ուշադրությունը դարձնել տվյալներին (կամ նախադրյալներին)։ Ի՞նչ է տրված: Ինչի՞ համար կարող են պետք գալ այդ տվյալները: Ի՞նչ կարելի է ստանալ այդ տվյալներից: Ապացուցման խնդիրների համար նմանատիպ հարցեր կան՝ ո՞րն է պայմանը (նախադրյալը). ինչի՞ համար կարող է պետք գալ այդպիսի պայմանը. ի՞նչ կարելի է ստանալ այդպիսի պայմանից: Այս հարցերը կարող են լինել մոտեցման սկիզբ, որը հիմնված է ճիշտ ուղղությամբ շարժվելու վրա: Տես 8-րդ գլխի 1 վարժությունը. այնտեղ պարզել ենք, և սա չպետք է մոռանալ, որ, ընդհանրապես ասած, հակառակ ուղղությամբ աշխատանքային պլան կազմելը պետք է գերադասել ուղիղ շարժվելու պլան կազմելուց):

Ցավոք, հաճախ պարզվում է, որ չենք կարողանում բավարար պլան կազմել՝ ո՛չ ուղիղ գնալու պլան, ո՛չ հառակ ուղղությամբ գնալու: Նման դեպքերում պահուստում ունենք ուրիշ հարցեր, որոնք կարող են մեզ օգնել խնդրի լուծմանը այլ մոտեցում գտնելուն. ահա դրանցից մի քանիսը (դրանք նույն հաջողությամբ կարելի է տալ նաև աշխատանքի սկզբում): Ի՞նչ տեսակի է դիտարկվող խնդիրը: Արդեն լուծված որևէ խնդրի հետ նույն տեսակի չէ՞: Արդյո՞ք նման չէ արդեն ծանոթ որևէ խնդրի: Փորձելով խնդիրը դասակարգել, ձգտելով գտնել նրա կապը կամ նմանությունը մեզ ծանոթ խնդիրների հետ, հնարավոր է հանդիպենք ծանոթ մեթոդի, որը հարմար կլինի դիտարկվող խնդրի համար, և արդեն սկսելու տեղ կլինի՝ կտեսնենք դեպի լուծումը տանող ճանապարհի առաջին մասը:

Փորձելով գտնել մեր խնդրին «ազգական» խնդիր՝ նշենք խնդիրների միջև այն կապերը («ազգակցական հարաբերությունները»), որոնք ավելի հաճախ են օգտակար լինում: Հայտնի՞ է ազգակից որևէ խնդիր: Կարո՞ղ եք տրվածին մոտիկ ինչ-որ խնդիր կազմել: Իսկ նմանատի՞պ խնդիր: Ավելի ընդհանո՞ւր խնդիր: Ավելի մասնավո՞ր խնդիր: Սակայն վտանգ կա, որ նման հարցերը ճիշտ ճանապարհից կարող են հեռացնել. այդ պատճառով սովորաբար ավելի օգտակար է լինում դրանք ավելի ուշ տալը, երբ խնդրի էությունը մեր գիտակցությունում լավ և հստակ է ամրացել, այսինքն՝ վախ չկա, որ գիտակցաբար հեռանալով խնդրից՝ կարող ենք այն ամբողջությամբ կորցնել տեսադաշտից:

§ 5. Հածում. միգուցե կա՞ խնդրի ավելի հուսադրող տեսանկյուն

Երբ գործ ունեք նյութական առակաների հետ (օրինակ, փորձում եք ճյուղը կտրել), մեքենայորեն ընտրում եք աշխատանքի համար առավել հարմար դիրք: Նման ձևով պետք է վարվել, երբ բախվում եք որևէ խնդրի. պետք է ձգտեք այնպիսի դիրք գրավել, որ հնարավոր լինի խնդրին մոտենալ ամենահարմար և ամենամատչելի կողմից: Մտքում քննում եք խնդիրը, գլխում պտտում այս ու այն կողմ՝ փորձելով կանգնել այն կողմից, որտեղից խնդիրը ամենահեշտն է թվում: Տեսանկյունը, որից սկսում եք խնդրի վրա աշխատելը, կարող է ամենանպաստավորը չլինել: Արդյո՞ք խնդիրը ձևակերպված է այնքան պարզ, այնքան հստակ, այնպես «հուշող», որքան հնարավոր է: Չե՞նք կարող խնդիրը այլ կերպ ձևակերպել:

Իհարկե, կցանկանայիք խնդիրն ավելի լավ ձևակերպել (այն ձևափոխել համարժեք խնդրի), որպեսզի ավելի ծանոթ, ավելի գրավիչ, ավելի մատչելի, ավելի հեռանկարային երևար:

Ձեր աշխատանքի նպատակն է լրացնել խզումը այն բանի միջև, ինչը պահանջվում է, և նրա, ինչ ունեք, անհայտը տվյալներին կապել, եզրակացությունը պայմանին (նախադրյալին): Չե՞ք կարող խնդրի ձևակերպումն այնպես փոխել, որ անհայտը և տվյալները, պայմանը և եզրակացությունը ավելի մոտենան:

Ձևափոխեք եզրակացությունը կամ նախադրյալը, կամ խնդրի երկու մասը միաժամանակ, բայց այնպես արեք, որ նրանք իրար ավելի մոտենան: Ձևափոխեք խնդրի անհայտը կամ տվյալները (պայմանը), կամ նույնիսկ խնդիրն ամբողջությամբ, բայց արեք այնպես, որ անհայտը և տվյալներն իրար ավելի մոտիկ հայտնվեն, քան առաջ էր:

Խնդրի լուծման առաջ գնալուն զուգընթաց ուսումնասիրվող պատկերի վրա նոր գծեր են հայտնվում. կառույցը, որ խնդիր լուծողը մտքում կանգնեցնում է, լրացվում է նոր մանրամասներով և կապերով: Խնդրի յուրաքանչյուր ձևափոխումը կարող է նոր տարրեր ներմուծել: Խնդրի ըմբռնման մեջ նոր նյութի ներարկման կարևոր ձևերից է սահմանումներին վերադառնալը:

Դիցուք՝ գործ ունենք հատած բուրգի հետ (ինչպես 7 գլխում), որպես օրինակ: Ի՞նչ է հատած բուրգը: Ինչպե՞ս է սահմանվում: Հատած բուրգ է կոչվում ամբողջ բուրգի մասը, որը մնում է բուրգից՝ նրա հիմքին զուգահեռ հարթությամբ փոքր բուրգ կտրելով: Այս սահմանումը երկու նոր մարմին է ներառում քննարկման մեջ՝ ամբողջական բուրգը և փոքր բուրգը, և կարող է օգտակար թվալ խնդրում մեկ կամ մյուս բուրգի, կամ միաժամանակ երկուսի ներառումը:

Վերադառնալով խնդրի պայմանում հանդիպող տարրերի սահմանումներին, դրանով նոր տարրեր ենք ներառում, որոնք իրենց հերթին նոր տարրեր են ներառում. շարունակելով նման ոգով գործելը խնդրի գաղափարները ավելի ենք լայնացնում: Խնդրի պայմանի այսպիսի ընդարձակումը հաճախ մեզ մոտեցնում է խնդրի լուծմանը, չնայած ոչ միշտ. երբեմն այն միայն խնդիրը ծանրացնում է ավելորդ մանրամասներով:

Խնդրի պայմանը ձևափոխելու շատ եղանակներ կան, որ արժանի են ուշադրության. դրանց մի մասը կիրառելի է միայն որոշ մասնավոր դեպքերում, մյուսները՝ ավելի համապիտանի են:

§ 6. Հածում. օգտակար տեղեկությունների փնտրտուք

Խնդրի լուծման ընթացքն էականորեն կախված է տվյալ խնդրի և արդեն կուտակած համապատասխան տարրերի միջև կապեր հաստատելուց: Երբ փորձում ենք խնդիրը այլ կերպ, ավելի հեռանկարային շարադրել, իրականում փնտրում ենք հենց այդպիսի կապ. ընդ որում ելակետն ինքը խնդիրն է, և փորձում ենք ճեղքել նրան շրջափակող ամպերը՝ աշխատելով «ներսից»: Բայց այդ կապը կարելի է փնտրել և մյուս ծայրից՝ փորձելով դրսում գտնել որևէ օգտակար տարր, այսպես ասած, խնդրին մոտենալ «արտաքինից»:

Դիտարկել երբևէ հավաքած մեր բոլոր գիտելիքները, անհնար է: Այդ պատճառով էլ պետք է սկսել հետազոտել գիտելիքի այն բնագավառներում, որոնց կապը դիտարկվող խնդրի հետ ավելի հավանական է:

Եթե բնագավառը, որին պատկանում է դիտարկվող խնդիրը, ձեզ ծանոթ է, պետք է իմանաք նրա «կարևոր կետերը»՝ փաստերը, որոնցից ամենայն հավանականությամբ պետք է օգտվեք: Դրանք այնպես նախապատրաստեք, ինչպես լավ բանվորը աշխատանքի համար իր սիրած գործիքները, այսինքն՝ այնպես, որ հեշտ լինի նրանցից օգտվելը:

Եթե գործ ունեք որոշման խնդրի հետ, հատուկ ուշադրության են արժանի նույն անհայտն ունեցող խնդիրները. այդպիսի խնդիրներից մեկը կարող է ելման կետ դառնալ հակառակ ուղղությամբ շարժվելու համար: Եթե ապացուցման խնդիր ունեք, որպես ելման կետ հատուկ ուշադրության են արժանի ձեզ հետաքրքրող խնդրի հետ նույն եզրակցությունն ունեցող թեորեմները:

Ո՞ր փաստերն են կարևոր: Կա՞ նման անհայտով խնդիր (ցանկալի արդեն լուծված): Կա՞ թեորեմ՝ նույն եզրակցությամբ (ցանկալի է, որ արդեն ապացուցված լինի): Մեծ է հնարավորությունը, որ այս հարցերը կօգնեն արդեն կուտակված գիտելիքից ինչ-որ օգտակար տարր գտնել. խորհուրդ է տրվում սկսել հենց դրանցից, եթե ցանկանում եք խնդրի լուծման համար պետքական տվյալները մեկտեղել: Եթե այս հարցերն անպտուղ լինեն, հավանաբար, ստիպված կլինեք ուշադրություն դարձնել ավելի բարդ կամ ավելի նուրբ փաստերին կամ դիտարկել արդեն լուծված խնդիրներ, որոնք ինչ-որ ընդհանուր տարր ունեն տրված խնդրի հետ. ամենևին պարտադիր չէ, որ դրանք լինեն անհայտը կամ եզրակացությունը: Անկասկած, գիտելիքների ձեր պահուստում կան տարրեր, որոնք կարելի է օգտագործել դիտարկվող խնդրում, բայց ինչպե՞ս են դրանք կապված: Ինչպե՞ս հասնեք դրանց: Կարող եք փորձել ընդհանրացումը, մասնավորեցումը, նմանարկումը. կարող եք փորփրել ձեր գիտելիքների այն ասպարեզը, որին պատկանում է խնդիրը, հատկապես, եթե ձեր գլխում այն այնքան էլ մեծ չէ:

Իհարկե, որքան ձեր գիտելիքը լայն է, և որքան կարգավորված, այնքան մեծ է հնարավորությունը, որ կգտնեք պետքական տարրերը (տես վարժ. 4)։

§ 7. Հածում. հնարավո՞ր է, որ պետք է իրավիճակը վերագնահատենք

Ենթադրենք, որ բավարարված չեք աշխատանքի ընթացքից: Ձեր գլխում ծնված տարբեր վարկածներ անհաջողության են մատնվել, ձեր փորձած տարբեր ճանապարհները փակուղի են մտել: Ձեր զննած պատկերը, խնդրի ամբողջական ըմբռնումը այդ վիճակում խառն է և մութ, ծանրաբեռնված մանրուքներով և միևնույն ժամանակ ամբողջական չէ. ինչ-որ էական տարր, ինչ-որ կարևոր օղակ պակասում է:

Գուցե դժբախտությունն այն է, որ ամբողջ ժամանակ քննել եք կողմնային ճանապարհներն ու փակուղիները, դրանով ձեզ ծանրաբեռնելով գործի հետ կապ չունեցող նյութով: Փորձեք վերադառնալ խնդրի սկզբնական, չգունազարդված դրվածքին. մի անգամ էլ դիտարկեք անհայտը, տվյալները և խնդրի պայմանը, խնդրի նախադրյալը և եզրակացությունը: Արդյո՞ք բոլոր պայմաններ եք հաշվի առել: Բոլո՞ր տվյալներն եք օգտագործելել: Բոլո՞ր նախադրյալներն եք հաշվի առել: Դրանց բոլո՞ր մասերն եք օգտագործել:

Այս հարցերը հատկապես տեղին են, եթե նախօրոք վստահ եք, որ անհայտը գտնելու համար պետք են խնդրի բոլոր տվյալները և խնդրի պայմանի բոլոր մասերը, կամ եզրակացության համար անհրաժեշտ է նախադրյալը ամբողջությամբ: Նույնիսկ եթե այդպիսի վստահություն չունեք և միայն կասկածում եք, որ բոլոր տվյալները և պայմանի բոլոր կետերը կամ նախադրյալները կարող են էական լինել, այդ դեպքում էլ նման հարցերը արդարացված կլինեն և կարող են օգուտ բերել: Նրանք հիշեցնում են, որ պետք փորձեք օգտագործել այն տվյալը կամ այն կետը, որը մինչ այդ դուրս եք թողել տեսադաշտից, և այդպիսով կարող է ձեզ հասցնել պակասող օղակին:

Դժբախտությունը կարող է նաև լինել, որ բավարար հստակությամբ չեք պատկերացնում խնդրի պայմաններում հիմնական տերմինների իմաստը: Ձեզ հասկանալի՞ են, ակնառու կերպով պատկերացնո՞ւմ եք խնդրի անբաժանելի մաս կազմող բոլոր հասկացությունները: Այս հարցը ձեզ կարող է ստիպել վերադառնալու որոշ հասկացությունների սահմանումների, և այդպիսով, միտք հղացնել լայնացնելու խնդրի դրվածքը. հույս կա, որ այն մեզ կօգնի ավելի լավ ձևակերպել խնդրի պայմանը և նոր օգտակար տարրեր գտնել:

§ 8. Հարցադրումներ անելու արվեստը

Նախորդ պարագրաֆներում տվեցինք խնդիր լուծողի տիպային մտավոր գործողությունների կամ մտավոր «քայլերի» ամփոփումը: Այդպիսի յուրաքանչյուր քայլի նկարագրությունը որպես գագաթնակետ ուներ հարց (կամ շեղատառ գրված խորհուրդ), որը կարող է ծառայել այդ կոնկրետ քայլի խտացված արտահայտություն, նրա պատկերը փոքր չափսերով: Կարևոր է հասկանալը, թե խնդիրը լուծողը (կամ ուսուցիչը) ինչպես կարող է օգտագործել այդ հարցերը:

Վերևում բերված հարցերից յուրաքանչյուրը, եթե տրվի ճիշտ ժամանակին և պատշաճ տեղում, կարող է խթանել ճիշտ պատասխան, ճիշտ գաղափար, մտքի լավ ուղղորդված շարժում, որոնք կարող են խնդրի լուծումը առաջ մղել: Այսպիսով, հարցը կարող է խթանիչի դեր խաղալ (նման դեպքերում քիմիկոսները ասում են «կատալիզատոր»), որը արագացնում է ցանկալի ռեակցիան: Նման հարցերը կարծես գաղափարների ինդիկատորներ լինեն:

Իհարկե, որոշ դեպքերում հնարավոր է, որ չիմանանք, թե հատկապես որ հարցը պետք է տալ: Այդ դեպքում կարող եք հարցերը հերթով փորձել, մինչև հասնեք այնպիսի հարցի, որ օգտակար կլինի: Այսպիսով, նախորդ պարագրաֆները կարող եք օգտագործել որպես պիտանի հարցերի կատալոգ, որպես դրանց թվարկում:

Սակայն, չի կարելի այդ թվարկումից օգտվել անկանոն ձևով՝ հարցերը պատահաբար ընտրելով, նաև չի կարելի նրանից մեխանիկորեն օգտվել՝ ընտրելով միշտ նույն հարցերը, անխախտ կարգով: Հարցերի այս ցուցակից օգտվեք, ինչպես արտադրությունում փորձառու բանվորը վարվում է իր գործիքների արկղի հետ: Նա ուշադիր հայացքով զննում է աշխատանքը, որը պետք է անի, հետո նոր ընտրում է գործիքը: Հնարավոր է, որ նա ստիպված լինի մի քանի գործիք փորձարկել, մինչև պետքականը գտնելը, բայց այդ դեպքում էլ նա գործիքները չի հանի պատահական կամ մեխանիկորեն հաստատված կարգով. նա դրանք ընտրում է մտածելով: Այդպես պետք է լինի պետքական հարցի ընտրությունը այս գլխում թվարկված հարցերի բազմությունից:

Իհարկե, բանվորը այդ վարպետությունը հավանաբար ձեռք է բերել եկարատև փորձի և ուրիշների աշխատանքին ուշադիր հետևելու շնորհիվ: Այդպիսի ճանապարհով կարող եք սովորել այստեղ հավաքված հարցերը կիրառելը: Դրանք օգտագործելը կարգավորող խիստ կանոն չկա: Սակայն, եթե այդ հարցերի ետևում կանգնած է ձեր անձնական փորձը, որը հենված է հաջողությունների և անհաջողությունների վրա, և եթե գիտեք նպատակը, որին ձգտում եք, հավանականությունը մեծ կլինի, որ լավ հարց կընտրեք:

Լավ բանվորի գործիքները միշտ սարքին վիճակում են և արկղում կարգով են դասավորված: Եթե այս գլխում նկարագրված հարցերը և դրանց հիմքում ընկած մտավոր տիպական գործողությունները ձեզ հայտնի են ոչ թե գրքերով, այլ փորձով, եթե դրանց դերը խնդիր լուծելու ընթացքում լավ եք հասկացել, մեծ հավանականություն կա, որ խնդիրներին կկարողանաք մոտենալ ավելի մասնագիտորեն, պակաս անճարտար, առանց օգտվելու պատահական հնարքներից, որոնք նման դեպքերում կօգտագործի անգետը:

Հնարավոր է, որ մտքի կարգավորվածության ցանկացած տեսակ հարցերի հավաքածու ունենալն ու դրանք ճիշտ օգտագործելու կարողությունն է: Բայց ինչպե՞ս կարելի է ուսումնասիրել հարցադրումների արվեստը: Արդյո՞ք այն ենթարկվում է ինչ-որ կանոնների:

12-րդ գլխին վերաբերող վարժություններ և լրացուցիչ ծանոթություններ

1. Փոխեք խնդրի ձևակերպումը: Մեր խնդրի նպատակն է ապացուցել (կամ հերքել) պնդումը. «Եթե A-ն ճշմարիտ է, ճշմարիտ է և B-ն»: Երբեմն հարմար է լինում խնդիրը ձևափոխել և փորձել ապացուցել (կամ հերքել) սկզբնական խնդրին համարժեք պնդումը՝ «Եթե B-ն կեղծ է, կեղծ է նաև A-ն» [1]: (Տես 9-րդ գլխի 10-րդ վարժությունը):

Ահա նմանօրինակ ևս մեկ իրավիճակ: Դիցուք՝ որոշման խնդրում x-ը անհայտն է, իսկ a, b, c, …, l –ը՝ տվյալները: (Այդ տվյալները և անհայտը, օրինակ, կարող են երկրաչափական պատկերի տարբեր մասերի չափսերը լինել): Հնարավոր է, որ ավելի նպատակահարմար լինի x անհայտի և տվյալներից մեկի, ասենք a-ի, դերերը փոխելը: Այդպես վարվելով՝ սկզբնական խնդրից անցնում ենք նոր խնդրի, որտեղ անհայտն է а-ն, իսկ տվյալները x, b, c, …, l։ (Տես 2-րդ գլխի 34, 35 և 36 վարժությունները):

Այստեղ դիտարկեցինք քննարկվող հարցի առարկայական բովանդակությունից անկախ ձևափոխությունների երկու տեսակ: Ձևափոխությունների այդպիսի տեսակների ուսումնասիրությունը, անկասկած, վերաբերում է էվրիստիկային:

2. Խնդիրը մաթեմատիկայի լեզվով արտահայտեք: Դեկարտի մեծ նախագծի ձևակերպումը, որը քննարկել ենք 2-րդ գլխի §1-ում, կարելի է խիստ սեղմել՝ հասցնելով շատ կարճ խորհրդի՝ «Ինչպիսին էլ լինի ձեր խնդիրը, այն ձևափոխեք մաթեմատիկական խնդրի՝ ներկայացնելով հանրահաշվական հավասարումների տեսքով»: Դեկարտի նախագիծը անիրականանալի դուրս եկավ, սակայն կարելի է վերակենդանացնել ընդհանրացման միջոցով՝ «Ձեր խնդիրը արտահայտեք մաթեմատիկայի լեզվով»: Այս խորհրդի հաջողությունը, իհարկե, կախված է մեթեմատիկայի լեզվի ձեր հարստությունից: Այսպես օրինակ՝ եթե գիտենք, որ կարող ենք օգտագործել ոչ միայն հանրահաշվական նշանները, ինչպես Դեկարտը, այլև դիֆերենցիալ և ինտեգրալ հաշվի նշանները, մեզ հասանելի խնդիրների քանակը զգալիորեն կաճի:

«Մաթեմատիկայի լեզու» հասկացությունը, իր լայն իմաստով, կարող է ընդգրկել բավականին հստակ տրամաբանական կառույցի ցանկացած տեսակ: Այդպիսի լայն ընկալման դեպքում «Արտահայտեք մաթեմատիկայի լեզվով» խորհուրդը, լինելով տեսականորեն անթերի, գործնականում կարող է անիմաստ թվալ, քանի որ կարող է միայն նշանակել «Փորձեք առավել պարզության հասնել» խորհուրդը [2]:

Սակայն, կա ավելի նեղ և նույնիսկ որոշ չափով անորոշ մեկնաբանություն, որը հաճախ ավելի օգտակար է լինում: Գրաֆիկները, դիագրամները կամ երկրաչափական պատկերները նույնպես մաթեմատիկական լեզվի տարատեսակներ են: Հաճախ օգտակար է լինում գծագիր անելը, խնդիրը երկրաչափական կառուցումների լեզվով արտահայտելը: Որոշ մարդիկ անհրաժեշտաբար կարիք են զգում իրենց գաղափարները երկրաչափական ինչ-որ նշանների միջոցով արտահայտելու:

3. Ապացուցեք հետևյալ պնդումը. եթե եռանկյան կողմը փոքր է մյուս երկու կողմերի միջին թվաբանականից, նրա դիմացի անկյունը փոքր կլինի մյուս երկու անկյունների միջին թվաբանականից:

(Որո՞նք են խնդրի գլխավոր մասերը: Դրանք արտահայտեք մաթեմատիկայի լեզվով՝ դրա համար օգտագործելով տարրական եռանկյունաչափության նշանակումները):

4. Գիտելիքի լավ կազմված և լավ կարգավորված պաշարը խնդիրը լուծողի կարևոր ակտիվն է: Այդ պաշարի լավ կազմակերպումը, որը հեշտ է մուտք բացում դեպի գիտելիքը, կարող է նույնիսկ ավելի կարևոր լինել, քան գիտելիքի աստիճանը: Ինչ էլ որ լինի, չափից ավելի գիտելիքը երբեմն վնասում է՝ խանգարելով խնդիրը լուծողին նկատել պարզ մոտեցումը. գիտելիքի լավ կազմակերպումը միշտ միայն օգտակար է:

Գիտելիքի լավ կազմակերպված պահուստում ավելի հաճախ պահանջվող օբյեկտները տեղավորվում են ամենահասանելի տեղերում. սովորաբար միասին օգտագործվող օբյեկտները միասին են պահվում, իսկ պիտակումը և տեղավորման կարգավորումը ծրագրվում է այնպես, որպեսզի հարմար լինի խմբավորել (զույգերով կամ միավորելով ավելի մեծ խմբերում) իրար հետ կապված օբյեկտները:

Իհարկե ձեր գրադարանում գրքերի կամ արկղում գործիքների խելամիտ դասավորումը օգտակար է, բայց շատ ավելի մեծ օգուտ կարող է բերել գիտելիքի խելամիտ դասավորումը ձեր հիշողության մեջ, և դա ակներևաբար շատ ավելի մեծ հոգածության է արժանի: Հիմա անցնենք խնդիրը լուծողի համար կարևոր կազմակերպման հարցերի:

1°. Յուրաքանչյուր կոնկրետ հարցում միշտ կան կարևոր փաստեր (կարևոր խնդիրներ, կարևոր թեորմներ), որոնք պետք է պահվեն ձեր հիշողության առջևի դարակում: Երբ ձեռնամուխ եք լինում խնդիրը լուծելուն, պետք է մոտակայքում, հենց ձեռքի տակ մի քանի կարևոր փաստ ունենաք. այդպես է փորձառու բանվորը դասավորում առավել հաճախակի օգտագործովող գործիքները իր համար ամենահասանելի տեղում:

Եթե ցանկանում եք տարրական երկրաչափությունից որևէ բան ապացուցել Էվկլիդեսի ոգով, որպես կարևոր փաստ՝ բնական է դիտարկելը եռանկյունների հավասարության երեք հայտանիշները և նմանության երեք հայտանիշները: Երբ, գործելով Դեկարտի ոգով, պատրաստվում եք տարրական երկրաչափության խնդիրը հանգեցնել հավասարումների համակարգի (տես գլուխ 2-ը), որպես կարևոր փաստ՝ կարելի է դիտարկել Պյութագորասի թեորեմը և նման եռանկյուններում հատվածների համեմատականության մասին թեորեմը: Նման ձևով ընտրվում են կարևոր փաստերը շարքերի զուգամիտության խնդիրներում և այլ խնդիրների բավականաչափ լայն դասերում:

2°. Ահա մեզ արդեն ծանոթ երկու հարց, որոնք նորից ու նորից խնդիր լուծողին օգնում են: Ինչպիսի՞ տվյալների միջոցով է հնարավոր որոշել նման անհայտը: Ո՞ր պայմանից կարելի է ստանալ այդպիսի եզրակացություն:.Հաշվի առնելով, որ այս հարցերը հատկապես հաճախ ենք օգտագործվում, պետք է կարծես «միասին պահել» նույն անհայտը ունեցող արդեն լուծած խնդիրները, ինչպես նաև միանման եզրակացություն ունեցող մեզ ծանոթ թեորեմները:

3°. Լա՞վ գիտեք արդյոք քաղաքը, որտեղ ապրում եք: Եթե շատ լավ գիտեք, պետք է կարողանաք քաղաքում երկու կետերը միացնող ամենակարճ ճանապարհն ընտրել, և իմանաք, թե տրանսպորտի ո՞ր տեսակներից է հարմար օգտվելը: Հենց այդպիսին պետք է լինի գիտելիքի ցանկալի կազմակերպումը. բնագավառում, որտեղ աշխատում եք, պետք է կարողանաք գտնել գործնականում հարմար կապ ցանկացած երկու կետերի միջև:

Գիտելիքի լավագույն կազմակերպմանը կարող է նպաստել իրար մոտիկ խնդիրների ընդհանուր ամփոփումը: Այսպես, օրինակ, այս գրքի առաջին մասը պարունակում է լայն տեսանկյունից դիտարկվող խնդիրներ, որոնք իրար հետ կապված են լուծման մեթոդի ընդհանրությամբ: Կարող ենք նաև դիտարկել խնդիրների շղթա, որոնք իրար հետ կապված են անհայտի կամ տվյալների ընդհանրությամբ կամ ինչ-որ նմանակությամբ և այլն:

Ինչպես հայտնի է, Էվկլիդեսը գրել է ոչ միայն «Հիմունքները», այլև մի քանի ուրիշ գիրք: Նրանցից մեկը՝ «Տվյալները», պարունակում է տարբեր տվյալների դիտարկումը, որոնց միջոցով սահմանվում են երկրաչափական առարկաները: Ուզում եմ հավատալ, որ Էվկլիդեսն իր «Տվյալները» գրել է, որպեսզի խնդիրը լուծողին օգնի հեշտ և մատչելի ձևով շարադրված երկրաչափական տեղեկություններից ընտրություն կատարելուն և նախատեսված է այն ըներցողների համար, ովքեր հաճախ են իրենց տալիս այս հարցը՝ ինչպիսի՞ տվյալների միջոցով կարելի է որոշել նման անհայտը:

5.      Ինչպիսի՞ տվյալների միջոցով կարելի է որոշել նման անհայտը: Հնարեք որոշման վերաբերյալ այնպիսի պարզագույն խնդիրներ, որտեղ անհայտը նկարագրվում է ստորև բերված արտահայտություններից մեկով.

1°. ... գտեք P կետը.
2°. ... գտեք AB հատվածի երկարությունը.
3°.  ... գտեք ABC եռանկայան մակերեսը.
4°.  ... գտեք ABCD քառանիստի ծավալը:

(Ամեն տեղ A, B, C, D տառերը կետեր են նշանակում):

6. Ի՞նչ պայմանից (նախադրյալից) կարելի այսպիսի եզրակացություն անել: Թվարկեք հարթաչափության պարզագույն թեորեմներ, որոնց եզրակացությունը համընկնում է ստորև բերված եզրակացություններից մեկի հետ.

1°. . . ., ապա AB=EF.
2° . . . , ապա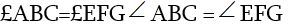 
3°. . ... ապա AB:CD = EF:GH
4°. ....   ապա AB < AC
(Ամեն տեղ A, B, C, D տառերը կետեր են նշանակում):

7. Քննարկվող հարցի հետ կապ ունեցող տեղեկություններ

Եթե a, b, c, d կողմերով և S մակերեսով քառանկյունը միաժամանակ և՛ ներգծյալ է, և՛ արտագծյալ (ներգծված է մի շրջանագծի և արտածված մեկ ուրիշի), ապա S²=abcd։

(Այս պնդման ապացույցը կարող է հեշտ կամ դժվար լինել՝ կախված այն բանից, թե այս հարցի հետ կապված որոշ պնդումների ծանոթ եք թե ոչ):

8. Եռանկյան և քառանիստի միջև նմանարկում

Ահա իրար նմանակերպ երկու խնդիր, որոնցից մեկը վերաբերում է եռանկյանը, իսկ մյուսը՝ քառանիստին.

• տրված եռանկյանը շրջանագիծ ներգծեք.
• տրված քառանիստին գնդոլորտ ներգծեք։

Իրար նմանակերպ թեորեմների և խնդիրների ուրիշ զույգեր թվարկեք: Նմանակերպ կլինե՞ն արդյոք դրանց լուծումները և ապացույցները, իսկ եթե ոչ, ինչպե՞ս կապված կլինեն իրար հետ:

9. Ձևակերպեք եռանկյուններին վերաբերող թեորեմ, որը նմանակերպ կլինի քառանիստների վերաբերյալ հետևյալ թեորեմին.

Քառանիստի երկու հանդիպակաց կողերի միջնակետերը միացնող հատվածն անցնում է այդ կողերին զուգահեռ ցանկացած հատույթի ծանրության կենտրոնով:

Կարո՞ղ է եռանկյան մասին թեորեմն օգնել քառանիստի մասին թեորեմն ապացուցելուն: Պատասխանեք համապատասխան հարցերին, որոնք վերաբերում են 10 և 11 վարժություններում բերված թեորեմներին:

10.  (Շարունակություն) Քառանիստի երկու հանդիպակաց կողերի միջնակետերով անցնող հարթությունը կիսում է քառանիստի ծավալը:

11.  (Շարունակություն) Քառանիստի երկնիստ անկյունը կիսող հարթությունը հանդիպակաց կողը բաժանում է հատվածների, որոնք համեմատական են այդ անկյունը կազմող նիստերի մակերեսներին:

12.  Ծանո՞թ եք արդյոք նմանատիպ խնդրի:

Լուծեք երեք հավասարումներով հետևյալ համակարգը x, y, z անհայտների համար (a, b, c մեծությունները տրված են).

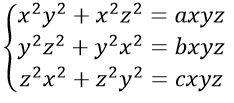
 (Այստեղ ունենք երեք անհայտներով երեք հավասարումների համակարգ: Այդ տեսակի համակարգերից ամենաուսումնասիրվածը գծային համակարգերն են: Կարո՞ղ եք «գծայնացնել» տրված համակարգը: Կարող ենք համակարգը գրել հետևյալ տեսքով.

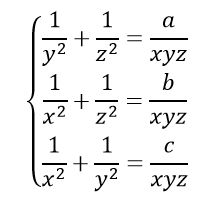
որը գծային է x^-2, y^-2, z^-2 նկատմամբ պայմանով, որ (երազենք…) xyz արտադրյալը մեզ հայտնի է: Լուծումը կունենա հետևյալ տեսքը

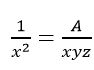 և այլն,

և այդպիսով մեր առջև նոր հորիզոն է բացվում (տեսնո՞ւմ եք այն):

13. Վերադարձեք սահմանումներին: Դիտարկեք երեք շրջանագիծ՝ f, f՛, v, որոնց կենտրոններն են համապատասխանաբար F, F՛, V: f և f՛ շրջանագծերը որոշակի են, իսկ v–ն փոփոխական, f՛ և v շրջանագծերը f–ի ներսում են, բայց ոչ իրար մեջ: Ապացուցեք հետևյալ պնդումը՝ եթե փոփոխական v շրջանագիծը շոշափում է f և f՛ շրջանագծերը, նրա կենտրոնների երկրաչափական տեղը էլիպս է:
(Ի՞նչ է էլիպսը)։ 

14. Մոտակա շրջապատի ուսումնասիրումը: Դուր եկա՞վ նախորդ խնդիրը (վարժություն 13): Իսկ լուծումը դուր եկա՞վ: Այդ դեպքում ուսումնասիրեք մոտակա շրջապատը. ծառի վրա գտել եք հասած և քաղցր մի խնձոր, բայց կարող է մի քանիսը:

Ձևափոխեք ձեր խնդիրը. կարող եք դիտարկել դրա ընդհանրացումը կամ մասնավոր դեպքերը, սահմանային դեպքերը, նմանակումները: Ինչ-որ նոր բան հայտնաբերելու և գիտահետազոտական աշխատանքի հմտություն ձեռք բերելու հնարավորություն ունեք:

Առաջադրվում է գտնել V  կետերի երկրաչափական տեղերը, որ համապատասխանում են f, f՛,  որոշակի շրջանագծերի և v փոփոխական շրջանագծերի մասին ձևափոխված պայմաններին:

1°. Մասնավոր դեպք: f և f՛շրջանագծերը համակենտրոն են:
2°. Սահմանային դեպք։ f-ը որոշակի ուղիղ է, f՛-ը՝ որոշակի շրջանագիծ (f-ից «դուրս», այսինքն f–ի հետ չհատվող), v–ն շոշափում է f-ը և f՛-ը:
3°. Նմանարկում: Երկու՝ f և f՛շրջանագծերը մեկը մյուսից դուրս են, իսկ v շրջանագծի շոշափումը այդ շրջանագծերին միևնույն բնույթն ունի. կա՛մ երկուսից էլ դուրս է, կա՛մ երկուսն էլ ընդգրկում է:
4°. 3° կետի մասնավոր դեպքը: Դիցուք f-ը և f՛-ը հավասար շրջանագծեր են, մնացածում 3° կետի պայմանները պահպանվում են:

Դիտարկեք նաև սկզբնական խնդրի կամ նրա տարբերակների այլ մասնավոր դեպքեր, սահմանային դեպքեր և նմանակումներ:

15. Ուշադրություն և գործողություն: 1° Իսկապես, ինչպես Դեկարտն էր պնդում (տես այս գլխի բնաբանը), մեթոդը ամբողջությամբ կազմված է բոլոր տարրերին ուշադրություն դարձնելուց, որոնք տրված հարցի հետ կապ ունեն (մեկը մեկից հետո և համապատասխան հաջորդականությամբ): Սակայն անկասկած է, որ խնդիրը լուծողի մեթոդական աշխատանքի զգալի մասը ուշադրության կենտրոնացումն է խնդրի հետ կապ ունեցող տարրերին (դրանք ընտրելով հաջորդաբար՝ մեկը մյուսից հետո) և դրանց համադրումներին:

«Ի՞նչ է անհայտը» հարցը և «Նայիր անհայտին» խորհուրդը նույն՝ խնդիրը լուծողի ուշադրությունը անհայտին սևեռելու նպատակն ունեն: Խնդիր լուծողը, աշխատելով մեթոդաբար, առաջ է շարժվում՝ կարծես ուղղորդվելով ներքին ձայնով.
- Դիտարկիր խնդիրն ամբողջությամբ:
- Նայիր անհայտին:
- Դիտարկիր տվյալները:
- Դիտարկիր պայմանները:
- Դիտարկիր տվյալներից յուրաքանչյուրը առանձին:
- Պայմանների յուրաքանչյուր կետը առանձին դիտարկիր:
- Հատկապես ուշադիր դիտարկիր այն տվյալը, որը դեռ չես օգտագործել:
- Հատկապես ուշադիր դիտարկիր պայմանի այն կետը, որը դեռ չես օգտագործել:
- Դիտարկիր այդ երկուսի համադրումը:
Եվ այդպես շարունակ:

2°. Ուշադրությունը կարող է գործողության սկիզբ լինել: Դիտարկեք անհայտը: Ո՞րն է անհայտը: Ինչպե՞ս կարելի է գտնել այդպիսի անհայտը: Ի՞նչ տվյալների միջոցով կարելի է որոշել այդպիսի անհայտը: Ծանո՞թ եք (կամ լուծել եք) նույն տեսակի անհայտ ունեցող խնդրի: Անհայտին սևեռված ուշադրությունը խնդիրը լուծողին ստիպում է փորփրել հիշողությունը՝ փնտրելով նույն անհայտն ունեցող լուծված խնդիրներ: Եթե այս ցանկը հաջող լինի, խնդիրը լուծողը կարող է փորձել լուծել՝ շարժվելով վերջից սկիզբ:

Չնայած այդպիսի դեպքը (անհայտին ուշադրություն դարձնելով խթանվող անդրադարձ աշխատանք) հատկապես հաճախ է հանդիպում և շատ օգտակար է, բայց խնդրի ուրիշ տարրերին էլ ուշադրության սևեռումը կարող է հասցնել օգտակար շփումների, և հետևաբար, հաջող գործողությունների: Այսպես, օրինակ, խնդրի ձևակերպման մեջ օգտագործված որևէ տերմինի ուշադրություն դարձնելը կարող է պահանջել վերադառնալ այդ տերմինի սահմանմանը, և այստեղից՝ ձևակերպման օգտակար փոփոխությանը, խնդրում նոր, օգտակար տարրեր ներմուծելուն:

3°. Հաջորդաբար ուշադրություն դարձնելով խնդրի տարբեր տարրերի և դրանց համադրումների, խնդիրը լուծողը հույս է ունենում դրանց մեջ հայտնաբերել այնպիսին, որ հնարավորություն կտա ինչ-որ խելամիտ գործողությունների, կամ (ավելի լավ) հենց այն, որը հնարավորություն կտա ամենախելամիտ գործողությունների: Նա հույս ունի գտնելու այնպիսի գաղափար, որ անմիջապես ցույց կտա, թե ինչ պետք է ձեռնարկել:

16. Արդյունավետ մտածողություն, ստեղծական մտածողություն: Մտածողությունը կարելի է արդյունավետ անվանել, եթե հասցնում է կոնկրետ խնդրի լուծմանը. մտածողությունը կարելի է ստեղծական անվանել, եթե միջոցներ է ստեղծում հետագա խնդիրներ լուծելու համար: Որքան մեծ է խնդիրների թիվը և լայն՝ բազմազանությունը, որոնց նկատմամբ կարելի է կիրառել ստեղծված միջոցները, այնքան բարձր է ստեղծական մտածողության մակարդակը:

Երբեմն խնդիրը լուծողի աշխատանքը կարելի է ստեղծական անվանել նույնիսկ այն դեպքում, որ նրան, չի հաջողվել խնդիրը լուծել. օրինակ՝ եթե նրա ջանքերը բացահայտել են միջոցներ, որոնք կիրառելի են ուրիշ խնդիրների նկատմամբ: Խնդիրը լուծողի աշխատանքը կարող է անուղղակի ստեղծական լինել. Օրինակ՝ եթե նա թողնում է չլուծված, բայց լավ խնդիրը, որը իր վերջո ուրիշների է հանգեցնում արգասաբեր գաղափարների:

Ինձ թվում է, որ հույները մեծ գործ են արել, որ մեզ թողել են անկյունը երեք հավասար մասերի բաժանելու խնդիրը, չնայած այդ խնդիրը չեն լուծել, և չնայած որ հաջորդ հարյուրամյակների ընթացքում այդ խնդիրը ապարդյուն անհավանական մեծ քանակի աշխատանքի աղբյուր է եղել: Նշենք, որ անկյունը երեք հավասար մասերի բաժանելու խնդիրը հակադրություն է բացահայտում, որ կիսել կարելի է ցանկացած հատված և անկյուն, մինչդեռ երեք հավասար մասերի կարելի է բաժանել (կարկինի և քանոնի օգնությամբ) միայն հատուկ ընտրված անկյուններ (ասենք 90⁰): Այս ճանապարհով գնալով՝ հետագայում հանդիպում ենք անկյունը 5, 7, 17 հավասար մասերի բաժանելու խնդիրներին, որոնք կապված են հավասարումները ռադիկալներով լուծելու խնդիրներին և, ի վերջո, Գաուսի, Աբելի և Գալուայի հայտնագործություններին, որոնք հանգեցրեցին անվերջ քանակությամբ խնդիրների նկատմամբ կիրառելի տեսությունների, որոնց մասին հույները, որ սկսել էին անկյունը երեք հավասար մնասերի բաժանելու խնդիրը, նույնիսկ չէին էլ կասկածում: 

13-րդ գլուխը

Թարգմանություն ռուսերենից 
Լուսանկարը` Արմինե Թոփչյանի

[1] Խնդրի այս ձևափոխումը «հակառակից ապացուցելու» մեթոդի բովանդակությունն է։
[2] «Մաթեմատիկական լեզու» տերմինի լայն ընկալման կարևոր մասը կազմում է ժամանակակից մաթեմատիակական տրամաբանության նշանային լեզուն, որի ստեղծումը կապվում է այս գրքում մի քանի անգամ նշված «համապիտանի մեթոդի» մասին Լեյբնիցի գաղափարների հետ: (Որոշ մաթեմատիկոսներ նույնիսկ հակված են նույնացնելու «մաթեմատիկական լեզու» հասկացությունը այդ նշանային լեզվի հետ)։ Սակայն այս գիրքը գրեթե չի շոշափում «մաթեմատիկական լեզվի» այդ տարատեսակը, քանի որ այն ամբողջությամբ վերաբերում է այն շրջանին, որը նախորդել է մաթեմատիկական տրամաբանության ծաղկմանը և մաթեմատիկայի մեթոդիկայում և մեթոդոլագիայում մաթեմատիկական տրամաբանության դերի և նրա նշանակումների մասին այժմ ընթացող լայն քննարկումներին: