Թվերի ընտրության և թվաբանական խնդիրների կազմության սկզբունքները
Primary tabs
Ի՞նչ է թվաբանությունը
Բ. Լ. Պաստերնակը գրել է, որ «նախապատրաստված անակնկալներն ավելի ձանձրալի են, քան թվաբանական խնդիրները»: Միտքը, թե թվաբանական խնդիրները ձանձրալի են, պատահական չէ. դրանց բազմաքանակ ժողովածուները լի են բթացնող վարժություններով, նախօրոք պատրաստված բաղադրատոմսերի կիրառումով, որոնք չեն ենթադրում ոչ մի մտավոր ջանք, և քննարկվող հարցերի (ինչպես նաև դրանց պատասխանների) նկատմամբ ոչ մի հետաքրքրություն չեն առաջացնում:
Ժամանակի այդ տաղտուկ» կորստից, որի ընթացքում, ինչպես ասում էր Մայակովսկին` «մարդն ախր մեծանում է հիմար և խոնարհ», խուսափելու պարզագույն ճանապարհը դպրոցից թվաբանությունն իսպառ վերացնելն է (իսկ «վայրկենապես քառակուսի արմատ հանել», ինչպես շարունակում է Մայակովսկին, կարող է և համակարգիչն անել):
Առաջարկվող գիրքը մեկ այլ տեսանկյան կողմնակից է. թվաբանական խնդիրները դրանք լուծող աշակերտներին ինքնուրույն մտածել սովորեցնելու հսկայական հնարավորություն են պարունակում՝ վերլուծելով ոչ ակնհայտ իրավիճակներ կյանքում, բնության և կյանքի տարբեր երևույթների սկզբնաղբյուրների բացահայտմանն ու բացատրմանը հասնելով (ինչպես նաև ընդունվող որոշումների հավանական հետևանքներին ճշգրիտ գնահատական տալով): Բանն այն է, որ հաճախ միևնույն (երբեմն պարզ) մաթեմատիկական գործողությունը թաքցնում է բացարձակապես տարբեր կենսական իրավիճակներ, իսկ թվաբանական խնդիրները այդ իրավիճակներում կողմնորոշվելու իդեալական ճանապարհ են:
Ահա այդպիսի խնդիրների մի շարք (այս խնդիրները վերցված են գրքի 21-23 էջերում ներկայացված մի երկու տասնյակ օրինակներից, որոնք վերաբերում են նույն գործողությանը).
- երեք խնձորից քանի՞սը կմնա, եթե ուտես դրանցից մեկը.
- քանի՞ սղոցումով է տախտակը երեք մասի բաժանվում.
- Տանյայի եղբայրների քանակը քանիսո՞վ է ավելի քույրերի քանակից, եթե Տանյան ունի երեք եղբայր ավելի, քան քույր.
- քանի՞ հարյուրամյակ առաջ է հիմնվել համալսարանը, որը հարյուր տարի հետո տոնելու է իր երեքհարյուրամյա հոբելյանը:
Այս չորս տարբեր հարցերի դժվարությունները լրիվ տարբեր են: Չնայած որ նրանք լուծվում են «միանման», դա կռահելը այդքան էլ հեշտ չէ: Ընթերցողին 3-1=2 հավասարության այլ ցուցադրություններով չձանձրացնեմ. գրքում ընթերցողն ինքը կգտնի և՛ դրանք, և՛ տասնյակ ավելի բարդ թվաբանական խնդիրներ: Այդ խնդիրները, իմ փորձի համաձայն, ավելի հեշտ լուծում են նախադպրոցականները, քան դպրոցական տարիքի երեխաները, իսկ դպրոցականները՝ ավելի հեշտ, քան ուսանողները, որոնք, ի դեպ, գերազանցում են իրենց պրոֆեսորներին:
Ֆիգարոն զուր չէր ասում, որ իր ամենօրյա աշխատանքն իրենից «ավելի շատ մտավոր ջանք է պահանջում, քան Գրենադան և Սևիլյան միասին ղեկավարելը»: Ստորև բերած թվաբանական խնդիրները ավելի շատ բան են սովորեցնում, քան հնգանիշ թվերի սյունակով գումարումը (կամ էլ երեքից մեկ հանելը, որով լուծվում են վերը նշված չորս խնդիրները):
Կարմիր գինով լի բաժակից մեկ գդալ լցրեցին սպիտակ գինով լի տակառի մեջ, իսկ հետո նույն գդալով խառնուրդից (ավելի վատ խառնված) մեկ գդալը ետ լցրին բաժակը: Արդյունքում ո՞րն է շատ՝ սպիտակ գինով լի տակառում կարմիր գինի՞ն, թե՞ սպիտակ գինին կարմիր գինով լի բաժակում:
Եզրափակելով ասածս, մեկ այլ թվաբանական խնդիր ներկայացնեմ (ինչպես արդեն փորձով ստուգել և հաստատել եմ, նախադպրոցականներն ավելի հմուտ են, քան նոբելյան մրցանակակիրները):
Գրապահարանի դարակի վրա որդը կրծել անցել է (կարճագույն ճանապարհով) Պուշկինի գրքի առաջին հատորի առաջին էջից մինչև կողքին գտնվող երկրորդ հատորի վերջին էջը: Յուրաքանչյուր հատորի էջերը միասին (հաստությամբ) 2 սանտիմետր են, իսկ յուրաքանչյուր կազմի հաստությունը` 2 միլիմետր: Ի՞նչ հեռավորություն է անցել որդը:
Այս խնդրի պատասխանը (4 միլիմետր) այնքան անսպասելի է, որ այն լուծող նախադպրոցականների ծնողները, սովորաբար չեն կարողանում ո՛չ գտնել, և ո՛չ էլ հասկանալ պատասխանը (դժվարացող ընթերցողին խորհուրդ կտայի գծել և տեսնել, թե ինչ տեսք ունեն գրապահարանի վրա իրար կողք կողքի գտնվող երկու հարևան հատորները): Դեկարտն արգելել է մաթեմատիկայում գծագրեր օգտագործել, որպեսզի նմանատիպ խնդիրները անհասանելի դառնան:
Չնայած առաջարկվող գիրքն ուղղված է ոչ թե խնդիր լուծողներին, այլ դրանք կազմողներին, դպրոցականները (որ չեն վախենում, չլսելու չեն տալիս արդեն իսկ հասկանալի և ակնհայտ փաստարկների փիլիսոփայական ընդհանրացումները) նույնպես կկարողանան այն օգտագործել. այս գիրքը սովորեցնում է ավելի շատ կողմնորոշվել կյանքում, քան կեղծ գիտական բարդաբանության մեջ:
Այս գիրքը գրողն իմ հայր Իգոր Վլադիմիրի Առնոլդն է (1900-1948), ով ԽՍՀՄ-ում մանկավարժական գիտությունների առաջին դոկտորն էր և մանկավարժական գիտությունների ակադեմիայի թղթակից անդամ:
Երբ նա մահացավ, ես 11 տարեկան էի, բայց նրանից մաթեմատիկական ոչ մի բան չեմ սովորել, նա ինձ ավելի մեծ սեր է ներշնչել ալպինիզմի, երկարատև ճամփորդությունների, փայտի վրա փորագրության արվեստի, ձկնորսության և դահուկավազքի նկատմամբ:
Իսկ երբ փորձեցի նրանից իմանալ, թե ինչու են դպրոցում սովորեցնում, որ երկու բացասական թվերի արտադրյալը դրական է ստացվում, հանրահաշվագետ Էմմի Նյոտերի այդ աշակերտն ինձ պատասխանեց. «Իրական թվերը բավարարում են օղակի աքսիոմներին (օրինակ (а + Ь)с = ас + Ьс), իսկ եթե երկու բացասական թվերի արտադրյալը դրական չլիներ, բաշխականության այս աքսիոմը կխախտվեր»:
Ես ոչ մի կերպ չէի հասկանում, թե ինչիս է պետք, որ աքսիոմները տեղի ունենան: Այդ ժամանակներից ի վեր ես չեմ ընդունում բոլոր տեսակի դեդուկտիվ-աքսիոմատիկ կարտեզիանական-դեկարտյան կառույցները, որպես հակագիտական դատարկաբանություն, որը հակասում է փորձերի վրա հիմնված բնական-գիտական մոտեցումներին:
Ինքս ինձ համար նշանների (-)•(-)=(+) օրենքը բացահայտեցի միայն մեկ տարի անց, երբ լուծում էի հետևյալ խնդիրը. «N քաղաքում մակընթացությունն այսօր կեսօրին է եղել: Ե՞րբ այն կլինի վաղը»: Օրերի և ամսի տևողությունները թույլ են տալիս հեշտորեն հասկանալ, որ տարբերությունը կազմում է մոտ 50 րոպե: Սակայն մակընթացությունը տեղի կունենա կեսօրից 50 րոպե առաջ, թե հետո` թույլ է տալիս որոշել միայն նշանների օրենքը (եթե գիտես, որ Երկիր մոլորակի պտույտը կատարվում է արևելքից արևմուտք և´ իր առանցքի, և´ Արեգակի շուրջը):
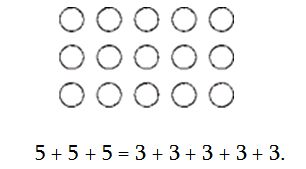
Թվաբանությունը բնությունը հասկանալու ամենակարճ ճանապարհն է, քանի որ այն գործ ունի ամենապարզ, ամենահիմնարար փորձարարական փաստերի հետ (օրինակ, քարերի հաշվումը տողերով և սյունակով միշտ բերում է միևնույն արդյունքին):
Հենց այս փորձարարական փաստերն են կազմում թվաբանության հիմքը, (որոնք հանրահաշվագետներն անվանում են «աքսիոմների հավաքածու» аЬ = Ьа և այլն):
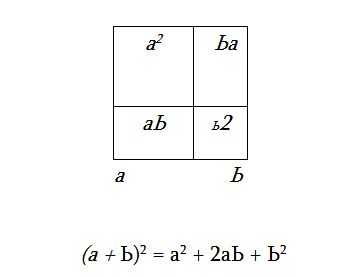
Այսպիսի դիտարկումների հանդեպ մեր ուղեղի ունակությունները համարժեք են շների մոտ Պավլովի պայմանական ռեֆլեքսների արտահայտմանը:
Օրինակ, Ժան-Ժակ Ռուսոյի օրինակին հետևելով, կտրելով а+Ь երկարության կողմով քառակուսին չորս ուղղանկյունների`ստանում ենք «Նյուտոնի երկանդամի» հանրահաշիվը սկսող թվաբանական թեորեմը:
Այնպես որ թվաբանական պարզագույն խնդիրները դեպի մաթեմատիկան և ամբողջ բնագիտությունը տանող ամենակարճ ճանապարհն է:
Վ. Ի. Առնոլդ
§ 1. Հարցադրում
Թվաբանական խնդիրները բավականին բազմազան և ոչ միանշանակ նպատակներ են հետապնդում, եթե բացառենք թվաբանական գործողությունների վարժանքի բնույթ ունեցողները: Նկատի ունենք նաև թվաբանության դասընթացի տեսական նյութի ամրապնդումը և մեծությունների միջև պարզագույն կախվածությունների հետ ծանուցումը, սովորողների հնարամտության մարզումը, ավելի ու ավելի բարդ «թվաբանական իրավիճակներում» նրանց ճիշտ կողմնորոշվելու ունակության զարգացումը: Սակայն առավել ստույգ այս նպատակները երբեք չեն արձանագրվել, խնդիրների դասակարգումը և ընտրությունը մինչ այժմ առավելապես բնորոշվել են պատմական սովորույթով` առավել ստույգ հաստատված սկզբունքներ չկան, որոնք թույլ կտային դատել այն մասին, թե հատկապես ինչի պետք է հասնել, ինչ կարգով, ինչ կարգի դժվարության խնդիրներ պետք է լուծվեն, ինչպիսի թեմատիկա և ձևավորում պետք է ունենան խնդիրները, ինչ կապի մեջ պետք է լինեն այս խնդիրները մաթեմատիկայի դասընթացի այլ մասերի հետ, ինչ պահանջներ պետք է ներկայացվեն թվային տվյալների ընտրությանը և այլն:
Այս բոլոր հարցերի վերաբերյալ մեթոդական գրականության մեջ կարելի է բավականին տարբեր և ոչ միանշանակ ցուցումների հանդիպել, սակայն դասավանդման պրակտիկայում հանդիպում են այս հարցերի բազմազան լուծումներ` ինչպես ծրագրերում, այնպես էլ համապատասխան ուսումնական ձեռնարկների բովանդակությունում:
Արդեն իսկ մինչհեղափոխական ժամանակներում միջին և տարրական դպրոցների առավել առաջադեմ և ակտիվ գործիչների միջավայրում ծագեցին և տարածում ստացան այն ուղղությունները, որ ձգտում էին դասավանդման պրակտիկայում արտացոլել նյութի և դասավանդման մեթոդների նորամուծությունների միտումները, որոնք բխում էին մաթեմատիկական ուղղությունների բավականին արագ աճի հետ և տեխնիկայում և ժամանակակից բնագիտության մեջ մաթեմատիկական մեթոդների տեսակարար կշռի կտրուկ աճի հետ:
Առավել սուր այս խնդիրները դրված են խորհրդային դպրոցի առջև, որ կոչված էր մինչ այժմ չտեսնված ծավալներով իրականացնել աշխարհում առաջին սոցիալիստական պետության աշխատողների` ժամանակակից գիտության և տեխնիկայի տիրապետման և ուսուցման նախապատրաստումը: Խորհրդային դպրոցի համար, այսպիսի իրավիճակն անտանելի է, երբ մաթեմատիկայի դասավանդման մեթոդները և բովանդակությունը, մասնավորապես հիմքերի հիմք հանդիսացող թվաբանությունը դեռ պահպանում են արդեն իսկ հնացած և կարծրացած ավանդույթները և սխեմաները և լիարժեք չեն համապատասխանում ժամանակի պահանջներին:
Դրությունը բարդանում է նաև նրանով, որ ուսուցման կոնկրետ պայմանները, նրա զանգվածայնությունը և միասնականացումը ոչ միայն զգալի, այլև համեմատաբար աննշան փոփոխություններ ներմուծելու ժամանակ ավելի զգույշ մոտեցումներ են պահանջում: Սակայն հենց դասավանդման զանգվածայնությունն ու միասնականացումը պարտադրում են անցկացնել նյութի մանրակրկիտ վերանայում, որպեսզի, ազատվելով այն ամենից, ինչը ավելորդ բալաստ է, մնացած ժամանակը և տեղը լրացվի իսկապես առավել անհրաժեշտ և պիտանի նյութով, առանց որի թվաբանության դասավանդումը միայն նվազագույն կերպով կկարողանա կատարել իր առջև դրված խնդիրները:
Մեզ թույլ տանք համեմատության համար հենվել այնպիսի առարկաների դասավանդման մեթոդիկաների մշակվածության վրա, որոնց մեջ անհրաժեշտ ունակությունների առկայությունը կամ էլ դրանց բացակայությունը հաստատվում են ոչ թե անուղղակի հատկանիշներով (հետագա ուսուցմանը ոչ բավարար պատրաստված լինելը, պրակտիկ հարցերի լուծման անկարողությունը), այլ անմիջականորեն ակնհայտ: Այստեղ կարելի է նշել, օրինակ, երաժշտության տեխնիկան կամ էլ օտար լեզուների ուսուցումը: Այստեղ չափազանց մանրակրկիտ են հավաքված և կազմված տարբեր տեսակի վարժությունները, հայտնի է, թե ինչի համար են դրանք պետք, ինչպես պետք է դոզավորել, ինչ արդյունքի պետք հասնել: Ուսումնասիրված են առավել հաճախ հանդիպող սխալները և կատարման թերությունները (կամ էլ լեզվի ուսուցման դեպքում, արտասանության, բառօգտագործման թերությունները և այլն), և դրանց վերացման համար հատուկ վարժություններ են մտածված: Բավական է ցանկացած երկու ձեռնարկ, մեթոդական երկու ուղեցույց համեմատել, որ համոզվենք` այս հարցում թվաբանությունը հետ է մնում բոլոր առարկաներից, չնայած որ հենց այստեղ պետք է ավելի պահանջկոտ լինենք և ավելի լավ մտածված և մշակված դետալացում պահանջենք:
Այսպիսով, մենք համարում ենք, որ մեզ մոտ ստեղծված պայմաններում թվաբանական խնդիրների բովանդակության, ձևի և դասակարգման մասնավոր հարցին ճիշտ մոտենալու համար անհրաժեշտ է (հաշվի առնելով ունեցած փորձարարական ամբողջ նյութը և ժամանակակից պայմաններում խորհրդային միջնակարգ դպրոցի աշակերտների մաթեմատիկական պատրաստության ընդհանուր խնդիրները) բավարար ամբողջականությամբ և կոնկրետությամբ որոշել` հատկապես ինչ մասնավոր նպատակների պետք է հասնել թվաբանական խնդիրների լուծման ժամանակ աշակերտների համապատասխան աշխատանքի արդյունքում:
Չնայած որ այս դրույթը կարող է տափակաբանություն թվալ, իրականում, թվաբանական նյութի նկատմամբ կոնկրետ կիրառման ժամանակ, այն ամենևին էլ պարզունակ չի լինում, քանի որ, ինչքան մեզ հայտնի է, նմանատիպ աշխատանք մեզ մոտ անհրաժեշտ մանրամասնությամբ դեռևս չի կատարվել: Առանձին, «սպառիչ ամբողջականության չհավակնող» անդրադարձները այս բնագավառում գրեթե պիտանի չեն. այստեղ անհրաժեշտ է հատկապես «ամբողջականության հավակնող» աշխատանք: Այս հոդվածի հեղինակը չի հավակնում այս աշխատանքը կատարելու ամբողջ ծավալով (և դժվար թե մեկ մարդու ուժերով հնարավոր լինի հասնել օբյեկտիվության անհրաժեշտ աստիճանի): Ավելի համեստ նպատակ է դրված` ուրվագծել այն բոլոր հիմնական դրույթները, որոնցից, հեղինակի կարծիքով, պետք է ելնել թվաբանության դասընթացում խնդիրները կազմելու և ընտրելու ժամանակ, մասնավորապես ուսուցման ուշ փուլերում:
§ 2. Թվանաբական խնդիրների ընտրությանը ու կազմելուն ներկայացվող պահանջների մասին
Սկզբում փորձեք կոնկրետացնել այն պահանջների բնույթը, որ մեր կարծիքով անհրաժեշտ է ներկայացնել պարտադիր նվազագույնում ընդգրկված թվաբանական խնդիրների բովանդակությանը: Նշենք, որ խնդիրների ընդհանուր քանակը, որ ուսուցման ընթացքում յուրաքանչյուր սովորող պետք է լուծի, այնքան էլ մեծ չէ: Այդ պատճառով տեղին է պահանջել, որպեսզի յուրաքանչյուր խնդիր (չէ՞ որ դրան կարող են հանդիպել սովորող միլիոնավոր երեխաներ) բոլոր առումներով այնքան ամբողջական լինի, որ հնարավոր լինի հիմնավորել և պաշտպանել միլիոնավոր տպաքանակի նրա իրավունքը: Կարծում ենք, որ այդ պահանջները կրտսեր և միջին դպրոցի վարժությունների ժողովածուում ներառված յուրաքանչյուր խնդրի վերաբերյալ միանգամայն բնական են: Խնդիրների հեղինակները պետք է կարողանան պատասխանել հարցերի, ասենք` այս տեսակի.
- Ի՞նչ նպատակ է հետապնդում տվյալ խնդիրը: Թվաբանության ուսուցման, դաստիարակության և մտքի վարժանքի հատկապես ի՞նչ տարրեր նկատի ունեն: Այդ նպատակների համար անհրաժե՞շտ է արդյոք հատկապես այդ խնդիրը ժողովածուի մեջ ներառելը: Ինչո՞ւ հատկապես այդպիսի, այլ ոչ ուրիշ մեծություններ, խնդրի հատկապես այդպիսի, այլ ոչ ուրիշ «բովանդակություն» է ընտրված: Ինչո՞ւ այդպիսի, այլ ոչ ուրիշ թվային տվյալներ: Համապատասխանո՞ւմ են դրանք արդյոք իրական իրավիճակին, որտեղ գուցե անհրաժեշտ լիներ այդպիսի խնդիր լուծել: Սովորողներին հետաքրքիր է արդյո՞ք առաջադրանքի բովանդակությունը, հարցադրումն արդյո՞ք գրավիչ է, բնական, առաջացնո՞ւմ է արդյոք մասնակիցների հետաարքրությունը պատասխանի կամ լուծման եղանակի հանդեպ, հատկապես ինչո՞վ: Հնարավոր չէ՞ այդ հետաքրքրությունը մեծացնել: Ե՞րբ հենց սովորողը ինքնուրույն կկարողանա լուծել տվյալ խնդիրը, դրա համար նա ի՞նչ պետք է հիշի, իմանա, կարողանա, պատկերացնի: Իսկ եթե չի կարողանում, ի՞նչի մասին է վկայում: Ուսուցիչն ինչո՞վ և ի՞նչ չափով պետք է նրան օգնի և ինչի՞ պետք է հասնի սովորողներից: Ինչպե՞ս է այդ խնդիրը կապված սովորողի նախորդ և հետագա աշխատանքի հետ, ինչո՞ւ է ժողովածուի հատկապես այս, այլ ոչ ուրիշ հատվածում զետեղված և այլն:
Առաջին հայացքից կարող է թվալ, որ խնդիր կազմողների նկատմամբ այսպիսի պահանջները չափազանց են: Կասեն` խնդիրների ժողովածու կա, սովորեցրեք երեխաներին լուծել այդ խնդիրները, և ամեն ինչ լավ կլինի, իսկ մանրամասներից ուսուցիչը գլուխ կհանի: Բայց ուզում ենք ընդգծել, որ այս հոդվածի հիմնական նպատակներից մեկը առաջին հերթին ցույց տալն է, թե որքանով է ուսուցման աչք ծակող թերությունների նկատմամաբ այդպիսի ավանդական հանդուրժողականությունն անընդունելի, ինչ հետևանքներ է այն թողնում, և երկրորդ, այդ թերությունների վերացման համար ուղիներ նշել:
Լուսանկարը` nonlin.ru-ից
- Բացվել է 3305 անգամ

