Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Սկիզբը

Գլուխ 2
Ոչինչ և ավելի քիչ մի բան, կամ որքան կարևոր է ազատ շարք ունենալը

Հնդկական համրանքի համակարգի հիմքում մեկից ինը թվանշաններն են: Նրանք ժամանակի ընթացքում ձևափոխվել և արդեն XVI դարի Եվրոպայում ժամանակակից տեսքն են ընդունել՝ 1, 2, 3, 4, 5, 6, 7, 8 և 9.

Կարող է թվալ` նոր բան չկա: Ե´վ հին հույները, և´ հին հրեաները թվերի համար տարբեր սիմվոլներ էին օգտագործում: Ե´վ մեկի, և´ մյուսի այբուբենի առաջին ինը տառն օգտագործում էին 1-9 թվերը նշանակելու համար: Հաջորդ ինը տառերը նշանակում էին՝ տասը, քսան, երեսուն և այդպես մինչև իննսուն թվերը: Հաջորդը ինը՝ հարուրյակները` հարյուր, երկու հարյուր, երեք հարյուր, մինչև ինը հարյուրը: Քսանութերորդ տառը հազար էր նշանակում: Այդպիսով, քսանութ տառը բավարար էր մեկից հազար թվային շարքը նշանակելու համար[1]: Երբ այբուբենի տառերը բավարար չէին լինում, ավելացնում էին հատուկ նշաններ կամ ձևափոխված տառեր:

Սակայն տառային նշանակումների կիրառումը հանգեցնում էր հասկացությունների շփոթի: Օրինակ, 15 թիվը հին հրեական գրությամբ «աստված» բառի առաջին երկու տառն է, այդ նույնը վերաբերում է նաև մի քանի այլ տառերի համադրությունների: Մյուս կողմից, յուրաքանչյուր բառի այս համակարգով կարելի էր որոշակի թվային նշանակություն վերագրել, ինչն արված էր աստվածաշնչյան շատ բառերի համար: Այս ընթացակարգն անվանում էին «գեմատրիա»:

Այս եղանակով շատ բառեր, այդ թվում և հատուկ անունները, ստանում էին հատուկ` առեղծվածային և գերբնական մեկնաբանություն: Այդպիսի մեկնաբանության ամենահայտնի օրինակը Հովհաննես Ավետարանիչի «Հայտնության» մեջ (այսինքն` Ապոկալիպսիսում) «գազան» բառն է, որը համապատասխանում է 666 թվին: Ավելի շուտ, որևէ տիրակալի անուն, որը այն ժամանակ նույնիսկ վտանգավոր էր ասել, հին հունական կամ հին հրեական այբուբենի տառերով նույնպես 666 թիվն էր նշանակում: Հնարավոր է, որ այդ տիրակալը Ներոն կայսրն էր: Այդ հին ժամանակներից մարդիկ հաճախ էին իրենց թշնամիների անունները թվերի տեսքով ծածկագրում:
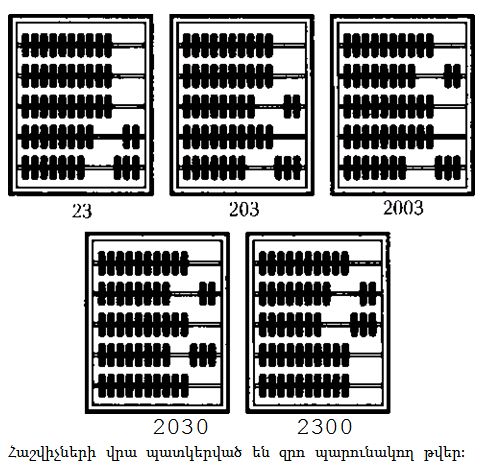
Հնդկական համակարգում, ի տարբերություն հին հրեականի և հին հունականի, բոլոր հնարավոր թվերը նշանակելու համար օգտագործում էին ընդամենը ինը թվանշան, ինչպես համրիչների դեպքում, ուր յուրաքանչյուր շարքում հատիկների նույն քանակն էր: Անհրաժեշտ էր, որ իրենց գրաված դիրքից կախված` թվանշաններին որոշակի արժեք տրվեր: Օրինակ, եթե ուզում ենք համրիչի վրա քսաներեք թիվը ցույց տալ, ներքևի (միավորների)շարքում տեղադրում ենք երեք հատիկ, իսկ հաջորդ՝ տասնյակների շարքում, երկու հատիկ: Հնդկական համակարգում այդ թիվը գրվում է 23, և երբ այն տեսնում ենք, միանգամից հասկանում ենք, որ տվյալ թիվը կազմված է երկու տասնյակից և երեք միավորից: Համապատասխանաբար, երեսուներկու թիվը կգրվի 32, որտեղ 3-ը տասնյակների քանակն է, իսկ 2-ը՝ միավորների: Քանի որ թվերի նշանակությունը կախված է դիրքից, ապա 32 և 23 թվերն բոլորովին տարբեր են:

Քիչ հավանական է, որ խորամանկ հին հույները չեն կարողացել այդպիսի համակարգ մշակել, չէ՞ որ նրանց հաջողվել է տարբեր բնագավառներում ամենատարբեր հայտնագործություններ անել: Նրանց, ինչպես նաև մյուսների համար (բացի հնդիկներից), մեթոդների զարգացման ճանապարհին իսկական խոչընդոտ էր համրիչի վրա դատարկ շարքի խնդիրը:

Պատկերացնենք, մեզ անհրաժեշտ է քսաներեքի փոխարեն երկու հարյուր երեք թիվը պատկերել: Համրիչի վրա ներքևի շարքում երեք հատիկ կդնենք, հաջորդ՝ տասնյակաների շարքում ոչինչ չենք դնի, և վերջապես հարյուրակների շարքում կդնենք երկու հատիկ: Իսկ ինչպե՞ս կգրվի այդ թիվը հնդկական համակարգում: Քսաներեքը գրում ենք 23, իսկ երկու հարյուր երեք թիվը, թվում է, թե նույն տեսքը պետք է ունենա՝ 23, բայց այս դեպքում 2 թիվը պետք է հարյուրակ նշանակի: Իսկ հիմա անցնենք հազարներին: Ինչպե՞ս համրիչի վրա երկու հազար երեք թիվը ցույց տանք: Ներքևի շարքում դնենք երեք հատիկ, տասնյակների և հարյուրյակների շարքերում ոչ մի հատիկ չենք դնի, և վերջապես հազարյակների շարքում երկու հատիկ դնենք: Իսկ ինչպե՞ս գրենք այդ թիվը հնդկական համակարգում: Նորի՞ց 23: Բայց այժմ երկուսը հազարյակների քանակն է նշանակում: Ի՞նչ է ստացվում. երեք տարբեր թվեր գրվում են նույն տեսքո՞վ: Ոչ, նրանք տարբեր ձևով են գրվում, և դա հնարավոր եղավ հնդիկների կողմից հաշվի համակարգում կատարած ամենամեծ կատարելագործման շնորհիվ: Ինչպե՞ս կարելի է այս երեք թվերը գրել, որ դրանք տարբերվեն: Կարելի է, ասենք, յուրաքանչյուր թվանշանի վերևում համապատասխան քանակի կետեր դնել, որը կնշանակի, թե որ կարգին է պատկանում տվյալ թվանշանը՝ հարյուրյակների, հազարյակների կամ տասնյակների: Օրինակ մեկ կետը՝ միավոր, երկուսը՝ տասնյակ, երեքը՝ հարյուրակ, չորսը՝ հազարյակ: Բայց գրառման այդպիսի համակարգը ծանր ու անհարմար է, և հնդկական համակարգը հիմնված է լրիվ ուրիշ սկզբունքի վրա:

Հին հնդիկների ամենամեծ ձեռք բերումը եղավ բացակա կարգի(այսինքն` համրիչի այն շարքի, որում ոչ մի հատիկ չկա) համար հատուկ նշան ներմուծելը: Արաբներն այդ նշանն անվանեցին «սիֆր», այսինքն դատարկ, անգլերենում անունը ձևափոխվեց «zero», իսկ ռուսերենում ադ նշանը ստացավ «ноль» անունը: Բայց ռուսերենում «սիֆր» բառը նույնպես մնաց: Նրանից առաջացան «цифра» (թվանշան), «шифр» (ծածկագիր), «шифро­вать» (ծածկագրել) բառերը:

Զրոն նշանակում են այսպես «0». Այժմ երկու հարյուր երեքը կարելի է գրել 203, իսկ երկու հազար երեքը՝ 2003, երկու հարյուր երեսունը՝ 230, երկու հազար երեսունը՝ 2030. Յուրաքանչյուր դեպքում մենք զրոյով նշանակում ենք հաշվիչի այն շարքը, որում հատիկները տեղաշարժված չեն:

Քսաներեքը կարելի է գրել 0023 կամ 00023 կամ նույնիսկ 000000023, բայց այդպես երբեք չեն անում: Հաճելի է գրել միայն առաջին իմաստալից նիշը, իսկ համրիչի վրա առաջին իմաստալից նիշից վերև բոլոր շարքերը հավասարեցվում են զրոյի):

Հենց զրո թվանշանի գյուտը, այսպես կոչված, արաբական թվանշանները հարմար և գործնական դարձրեց: Այդ գյուտը իսկական հեղափոխություն դարձավ: (Տարօրինակ է, որ «զրոյի», այսինքն` «ոչնչի» հայտնագործումը մարդկության հետագա զարգացման համար այդքան կարևոր դարձավ: Բայց ավելի տարօրինակ է, որ հին դարերի շատ հայտնի մաթեմատիկոսներ չէին էլ մտածել այդ «ոչնչի» մասին):

Հաշիվների փոխանցումը թղթին

Երբ հաշվում ենք` օգտագործելով արաբական թվերը, առաջինը, ինչ պետք է անենք, զրոյից մինչև ինը թվերի գումարները հիշելն է: Ինչպե՞ս ենք հաշվել սովորում: Սկզբում հիշում ենք, որ 1+1=2, 2+3=5, 4+5=9, 6+7=13 և այլն: Շատ կարևոր է յուրացնել, որ 0+0=0:

Երբ հաշվում ենք համրիչներով, ոչինչ հիշելու կարիք չկա: Անհրաժեշտ է միայն մեկից մինչև տասը հաշվել սովորել: Այս փուլում թղթի վրա գրած թվերի օգնությամբ հաշվարկների առավելությունը դեռևս նկատելի չէ: Թվում է, թե համրիչներն ավելի հարմար են:

Իսկ հիմա փորձենք երկու մեծ թվեր գումարել, օրինակ 5894 և 2578. Այն, ինչ անհրաժեշտ է՝ տասի սահմաններում թվերը գումարել կարողանալն է: Սկզբում թվերը տրոհենք միավորների, տասնյակների, հարյուրյակների և հազարյակների, այսինքն՝ կարգերի: 5000 և    800 և     90 և 4 գումարած 2000 և 500 և 70 և 8` 7000 և 1300 և 160 և 12: Այժմ տրոհենք 1300 թիվը` 1000 և 300, 160–ը՝ 100 և 60, իսկ 12-ը՝ 10 և 2. Հետո պետք է միայն հազարները հազարներին ավելացնել, հարյուրները՝ հարյուրներին, տասնյակները՝ տասնյակներին: Արդյունքում կստանանք` 8000 և 400 և 70 և 2, այսինքն` 8472.

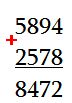
Պարզեցումն այն է, որ չենք գրում «զրոները» և «միավորներ» ենք փոխանցում հաջորդ կարգ, այսինքն` տասնյակները տեղափոխում ենք տասնյակների շարք և այլն:

Հանումը գումարման հակառակ գործողությունն է: Ենթադրենք, որ պետք է 531-ից 298 հանել: Այս դեպքում նույնպես թվերը ներկայացնում ենք կարգային գումարելիների տեսքով` 500 և 30 և 1 հանած 200 և 90 և 8:

Սկզբում կարող է թվալ, որ պետք է 1-ից 8 հանենք, և 30-ից՝ 90. Բայց այդպես չէ, մենք կարող ենք մեկ տասնյակ և մեկ հարյուրյակ պարտք վերցնենք հաջորդ կարգերից: Աղյուսյակը նոր տեսքով գրենք. 400 և 120 և 11 հանած 200 և 90 և 8` 200 և 30 և 3:

Այսպիսով, պատասխանը՝ 233:

Երբ կատարում ենք սյունյակներով հանում, հենց այս սկզբունքին ենք հետևում, չնայած գրառման ձևն ավելի պարզեցված է լինում:

Համրիչով հաշվելուն սովոր մարդը այս գործողությունն ավելի արագ կկատարի, քան այս երկու թվերի տարբերությունը հաշվող միջին սովորողը` թղթի վրա: Բայց համրիչը, ամեն ինչից բացի, մեխանիկական հմտությունների զարգացում է պահանջում:

Միևնույն ժամանակ, երբ սյունյակով ենք հաշվում, գրանցում ենք բոլոր քայլերը, այս դեպքում հեշտ է ստուգում կատարելը: Հաշվիչ օգտագործելիս դա չի կարելի անել: Սյունյակներով հաշվելու մեթոդն այնքան արդյունավետ է հաշվիչներով հաշվելուց, որքան թվերի հաշվիչներով ցուցադրումը՝ մատներով ցույց տալուց:

Հատում ենք զրոյի սահմանը

Թվաբանություն սովորող յուրաքանչյուր առաջին դասարանցի գիտի, որ կարելի է ցանկացած երկու թիվ իրար գումարել: Գիտի նաև, որ այդ կանոնը հանմանը չի վերաբերում: Կարելի է 7-ից 5 հանել և ստանալ 2: Կարելի է 7-ից 7 հանել և 0 ստանալ: Իսկ կարելի՞ է 7-ից 8 հանե՞լ: Հին Հունաստանում այդ հարցին բացասական էին պատասխանում: Ինչպե՞ս կարելի է գործողություն կատարել, որի արդյունքը ոչնչից փոքր լինի: Ախր «ոչինչ»-ը ծայրագույն սահմանն է, որից այն կողմ գնալու տեղ չկա:

Այս տեսակետն իշխում էր մինչև 1500-ական թվականները: Իսկ մեր օրերում միանգամայն ակնհայտ է թվում, որ կարող են գոյություն ունենալ «ոչնչից», այսինքն՝ զրոյից, փոքր թվեր: Ենթադրենք, թե յոթ դոլար ունես, իսկ ընկերդ հանկարծ մոտենում և հիշեցնում է, որ ութ դոլար պարտք ունես: Ազնիվ մարդ լինելով, դու իսկույն վերադարձնում ես յոթ դոլարը և ասում, որ մնացած մեկ դոլարը կվերադարձնես՝ հենց որ գումար ունենաս:

Այժմ «ոչնչից» քիչ ունես. դրամ չունես, և հակառակը, դեռ մեկ դոլար էլ պարտք ես: Այլ կերպ ասած, եթե յոթից հանենք ութ, կստանանք զրոյից մեկով քիչ թիվ: Ի՞նչն է այստեղ դժվար կամ անհասկանալի:

Պատկերացնենք, պատրաստվում եք քաղաք գնալ, որը ձեր գտնվելու վայրից յոթ կիլոմետր հարավ է: Եվ այսպես, դուք գնում եք հարավ: Անցնում եք մեկ կիլոմետր, և ձեզ մնում է վեց կիլոմետր անցնելու, անցնում եք երկու կիլոմետր, մնում է ևս հինգը: Անցնում եք յոթ կիլոմետր, և ահա տեղում եք: Մինչև քաղաք մնաց անցնելու զրո կիլոմետր:

Բայց դուք այնքան ցրված եք (կամ այնքան համառ), որ շարունակում եք շարժվել ևս մեկ կիլոմետր դեպի հարավ: Եվ այսպես, անցաք ութ կիլոմետր և հայտնվեցիք քաղաքից մեկ կիլոմետր հարավ: Մինչև քաղաք յոթ կիլոմետր էր, իսկ դուք անցաք ութը: Այսինքն՝ դուք ստանում եք զրոյից փոքր թիվ: Իհարկե դուք կարող եք ասել, որ հեռավորությունը նորից սկսեց մեծանալ: Բայց չէ՞ որ հիմա շարժվում եք հակառակ ուղղությամբ: Մի՞թե դա նույնն է:

Իրավիճակը հստակեցնելու համար նկարենք ուղղաձիգ գիծ և նրա վրա կետով նշենք քաղաքի տեղը: Այդ կետը կհամարենք ելման կետը կամ զրոն: Այժմ ուղղի վրա նշենք մի քանի հավասար հատվածներ՝ զրոյական կետից վերև և ներքև: Թող յուրաքանչյուր հատված համապատասխանի մեկ կիլոմետրի: Հաշվարկման կետից վերև ընկած թվերը (այսինքն` քաղաքից հյուսիս) կանվանենք սովորական (կամ դրական) իսկ դեպի ներքև՝ (այսինքն` քաղաքից հարավ) զրոյից փոքր կամ բացասական թվեր:

Հիմա դրականը թիվը բացասական թվից տարբերելու համար մեզ հատուկ նշան է անհրաժեշտ: Սովորաբար դրա համար օգտագործում են այն մեթոդի վրա հիմնված նշանակումների համակարգը, ըստ որի հնարավոր է այդ թիվն ստանալ: Ցանկացած դրական թիվ ստանում ենք ուրիշ դրական թվեր գումարելով: Դրական թվի խորհրդանիշ է հանդիսանում «+» նշանը, դրա համար էլ դրական թվերը նշանակում ենք +1, +2, +3 և այլն: Հենց «դրական թիվ» անվանումն ասում է այն մասին, որ այդ թիվը իրականում գոյություն ունի:

Բացասական թվերը ստանում ենք հանման արդյունքում, ասենք, (2 - 3) հանման դեպքում ստանում ենք զրոյից մեկ միավոր փոքր թիվ: Դա նշանակում են -1: Այսպիսով, բացասական թվերը նշանակում են -1, -2, -3 և այլն[2]:

Պատահական չէ, որ զրոյից փոքր թվերը ստացել են բացասական անվանումը: Նույնիսկ, երբ մաթեմատիկոսները յուրացրել էին զրոյից փոքր թվերի հետ գործողությունները, անհրաժեշտ էր շեշտել, որ այդ թվերն իրականում գոյություն չունեն:

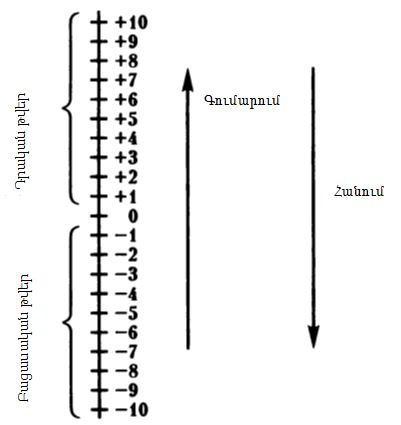
Ուշադրություն դարձրեք, որ զրոն ոչ դրական թիվ է, ոչ էլ բացասական: Այժմ ունենք նշագիծ ուղղաձիգ ուղիղ, այսինքն` սանդղակ, և կարող ենք այն օգտագործել գումարման և հանման գործողությունների համար: Քանի որ դրական թվերը մեծանում են սանդղակով դեպի վեր շարժվելիս, իսկ դրական թվերի գումարման գործողությունները հանգեցնում են թվերի մեծացմանը, կարող ենք համարել, որ գումարումը սանդղակով դեպի վեր շարժումն է:

Հանումը գումարման հակառակ գործողությունն է, դրա համար էլ հանումը սանդղակով դեպի վար շարժումն է:

Ենթադրենք, թե պետք է +2-ին գումարենք +5: Այս արտահայտությունը կարելի է գրառել հետևյալ ձևով` (+2)+(+5): Փակագծերն օգտագործեցինք գումարման գործողության նշանը դրական թվերի նշանից տարբերելու համար: Բայց քանի որ մենք վարժվել ենք, որ սովորաբար գործ ունենք դրական թվերի հետ, հաճախ նրանցից առաջ «+» նշանն ուղղակի չենք գրում: Այդ դեպքում ստանում ենք՝ 2+5: Անհրաժեշտ է «+» նշանը դրական թվի առջև դնել միայն այն դեպքերում, երբ հատուկ ուշադրություն է հրավիրվում թվի նշանին:

Այժմ մեր սանդղակի վրա երկու հատված բարձրանանք դեպի վեր: Դա 2 թիվն է: Ավելացնենք ևս 5 հատված և կանգ առնենք 7-ի վրա, այսինքն` 2+5=7: Կարող ենք սկսել 5-ից և բարձրանալ երկու հատված: Էլի 7 կստանանք: Այստեղ ձեր ուշադրությունը նորից եմ հրավիրում այն փաստին, որ գումարելիների տեղերը փոխելիս գումարը չի փոխվում:

Այժմ հանումով զբաղվենք: Ենթադրեն, պետք է 5-ից 2 հանենք: Սանդղակի 5 կետից երկու հատված շարժվում ենք դեպի ներքև և հասնում ենք 3 կետին: Այսպիսով, ստանում ենք՝ 5-2=3:

Հիմա պարզենք, թե ինչպես վարվենք բացասական թվերի հետ: Կարո՞ղ ենք նրանց հետ գործողություններ կատարել, ինչպես դրական թվերի հետ: Եթե այո, ապա նրանք շատ օգտակար կլինեն, չնայած որ «իրական» թվեր չեն: Եվ իսկապես, բացասական թվերը լայն կիրառություն գտան ոչ միայն գիտության մեջ և ինժեներական գործում, այլև առօրյա գործունեության մեջ: Դրանք գործածվում են, օրինակ, հաշվապահության մեջ, ուր մուտքերն ու եկամուտները նշանակում են դրական թվերով, իսկ ծախսերը՝ բացասականներով:

Բացասական թվերով գործողություններ ենք կատարում

Սկսենք հասարակ օրինակից: Պարզենք, թե ինչի է հավասար 2–5 արտահայտությունը: +2 կետից հինգ հատված իջնենք, երկուսը` մինչև զրոն և երեքը՝ զրոյից ներքև: Կկանգնենք -3 կետի վրա: Այսինքն` 2-5=-3: Իսկ հիմա ուշադրություն դարձրեք, որ 2-5 ամենևին հավասար չէ 5-2: Եթե թվերի գումարման դեպքում նրանց դիրքը նշանակություն չունի, հանման դեպքում լրիվ ուրիշ է: Թվերի դասավորությունը նշանակություն ունի:

Այժմ դիտարկենք սանդղակի բացասական մասը: Ենթադրեք, որ անհրաժեշտ է -2-ին ավելացնել +5: Այս պահից սկսած` մինչև այս գլխի վերջը դրական թվերի առջև կդնենք  «+» նշանը և կվերցնենք փակագծերի մեջ ինչպես դրական, այնպես էլ բացասական թվերը, որպեսզի չշփոթենք գումարման և հանման գործողությունների նշանների հետ): Այժմ մեր խնդիրը կարելի է գրել այսպես՝ (-2)+(+5): Որպեսզի այն լուծենք, պետք է -2 կետից բարձրանանք հինգ հատված և կհասնենք +3 կետին: Այս խնդրի մեջ կա՞ արդյոք գործնական իմաստ: Իհարկե կա: Պատկերացրեք, որ 2 դոլար պարտք ունեք, իսկ աշխատել եք 5-ը: Այսպիսով, երբ դուք ձեր պարտքը վերադարձնեք, ձեզ մոտ 3 դոլար կմնա: Կարելի է այդպես շարժվել դեպի ներքև սանդղակի բացասական մասով: Պատկերացրեք, թե պետք է -2-ից 5 հանենք, կամ (-2)-(+5): Սանդղակի -2 կետից իջնում ենք ներքև հինգ հատված և հասնում -7 կետին: Ինչպիսի՞ գործնական իմաստ կա այս խնդրում: Ենթադրենք, որ 2 դոլար պարտք ունեք և ստիպված եք ևս 5դոլար պարտք անել: Այժմ ձեր պարտքը 7 դոլար կլինի:

Տեսնում ենք, որ բացասական թվերով էլ կարելի է գումարման և հանման գործողություններ կատարել, ինչպես դրական թվերով:

Իհարկե, դեռ ոչ բոլոր գործողություններն ենք յուրացրել: Բացասական թվերին գումարում և նրանցից հանում էինք միայն դրական թվեր: Իսկ ինչպե՞ս վարվենք, երբ պետք է բացասական թվերը գումարել կամ բացասական թվից հանել բացասական թիվ: Գործնականում դա նման է պարտքերի գործողություններին: Պատկերացրեք, որ ձեր պարտքից 5 դոլար դուրս են գրել, դա նույնն է, եթե դուք 5 դոլար ստանայիք: Մյուս կողմից` եթե ես ինչ-որ ձևով ստիպեի ձեզ հանձն առնել ուրիշի 5 դոլար պարտքը, դա նույնն է, թե ձեզանից վերցնեի այդ 5 դոլարը: Այսինքն -5 հանելը նույնն է, ինչ ավելացնել +5. Իսկ ավելացնել -5 նույնն է, ինչ հանել +5:

Սա մեզ թույլ է տալիս ազատվել հանում գործողությունից: Իսկապես, «5-2»-ը նույնն է, ինչ (+5)-(+2), կամ էլ մեր կանոնի համաձայն (+5)+(-2): Ե´վ այս, և´ մյուս դեպքում նույն արդյունքն ենք ստանում: +5 կետից պետք է ցած իջնենք երկու հատված և կստանանք +3: Իսկ 5-2 դեպքը ակնհայտ է, քանի որ հանումը դեպի ներքև շարժումն է:

 (+5)+(-2) դեպքում դա պակաս ակնհայտ է: Թիվ ենք ավելացնում, դա նշանակում է շարժում դեպի վերև,բայց բացասական թիվ ենք ավելացնում, այսինքն` լրիվ հակառակ գործողություն է, և այդ երկու փաստերը համադրելով` նշանակում է, որ պետք է շարժվենք ոչ թե սանդղակով վերև, այլ հակառակ ուղղությամբ, այսինքն` վար: Այսպիսով նորից +3 կստանանք:

Ըստ էության, ինչո՞ւ է պետք հանումը գումարումով փոխարինել: Ինչո՞ւ «հակառակ իմաստով» վերև շարժվել: Ավելի հեշտ չէ՞ արդյոք ուղղակի ներքև շարժվելը: Պատճառն այն է, որ գումարման ժամանակ գումարելիների կարգը նշանակություն չունի, մինչդեռ հանման դեպքում շատ կարևոր է:

Արդեն պարզել էինք, որ (+5)-(+2)-ը նույնը չէ, ինչ (+2)-(+5): Առաջին դեպքում պատասխանը +3 է, իսկ երկրորդում՝ -3. Մյուս կողմից և´ (-2)+(+5)-ը, և´ (+5)+(-2)-ը արդյունքում +3 են տալիս: Այսպիսով, հանման գործողությունից հրաժարվելով և անցնելով գումարմանը, կարող ենք գումարելիների դասավորության պատահական սխալներից խուսափել: Նման ձևով կարելի է գործել բացասական թվի հանման դեպքում՝ (+5)-(-2)-ը նույնն է, ինչ (+5)+(+2). Երկու դեպքում էլ արդյունքում +7 ենք ստանում: Սկսում ենք +5 կետից և շարժվում «ներքևին հակառակ ուղղությամբ»,այսինքն` վերև: Հենց այդպես էլ վարվեցինք, երբ լուծում էինք (+5)+(+2) արտահայտությունը:

Հանումը գումարումով փոխարինելը սովորողներն ակտիվորեն օգտագործում են, երբ սկսում են հանրահաշիվ ուսումնասիրել, դրա համար էլ այս գործողությունն անվանում են «հանրահաշվական գումարում»: Իրականում դա այնքան էլ արդար չէ, քանի որ այդպիսի գործողությունն ակնհայտորեն թվաբանական է, ոչ թե հանրահաշվական: 

Շարունակությունը

Թարգմանություն ռուսերենից