Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Գլուխ 1
Թվեր և ... թվեր

Թվերի նշանակումը

Երկրի վրա մարդիկ միակ արարածները չեն, որոնց հասու է թվերի իմացությունը: Կենդանիներին նույնպես կարելի է սովորեցնել առարկաների քանակը տարբերել: Բնականաբար, ոչ ոք չի մտածում, որ կենդանիները գիտակցաբար են հաշվում, բայց անշուշտ, կարողանում են թվերը տարբերել:

Մեզանից շատերը խաղաքարտերով խաղալիս երբեք ուշադրություն չեն դարձնում վերևի ձախ անկյունում գրված փոքրիկ թվերին: Նույնիսկ միջին խաղացողը դրա կարիքն առանձնապես չի զգում:

Խաղի նկարագրության մեջ էլ թվեր չեք գտնի: Եվ դա ոչ ոքի չի անհանգստացնում: Սովորաբար խաղաքարտի թիվն իմանում ենք առաջին հայացքից՝ առանց հաշվելու:

Մարդկության պատմության որոշիչ պահը եկել է այն ժամանակ, երբ պարզ օրինակներն արդեն բավարար չէին:

Դժվար չի նայել քարանձավի ներսը և համոզվել, որ երկու երեխաներն էլ տեղում են, կամ էլ աչք գցել քարե կացիններով դարակին` վստահանալու, որ բոլոր չորսն էլ անվնաս են: Բայց պահանջվեց ավելի բարդ տեղեկություն, և ինչ-որ պահի մարդը որոշեց, որ անհրաժեշտ է թվեր օգտագործել: Ասենք, պետք լինի հարևանի մոտ գնալ ու ասել. «Լսի´ր, ծերուկ, պատահաբար, իմ քարե կացիններից մեկը չե՞ս վերցրել, երբ նախորդ անգամ իմ քարանձավ էիր մտել»: Եվ եթե հարևանը պատասխանի. «Աստված քեզ հետ, ինչո՞ւ ես այդպես մտածում», կարելի է հետևյալ փաստարկը բերել.  «Լսիր, ընկեր ջան, մինչ քո գալը չորս կացին ունեի, իսկ քո գնալուց հետո երեքն է մնացել»:

Այսինքն, պարզվեց, որ շատ հարմար է, երբ յուրաքանչյուր թիվ անուն ունի:

Անկասկած, սկզբում միայն մի քանի անուն էին մտածել, որոնք բավարար էին միայն պարզագույն տեղեկություններ ընդհանրացնելու համար: Որոշ պարզունակ ցեղեր անգամ այսօր չունեն երկու կամ երեք թվերի անուններից ավելի: (Դա, իհարկե, չի նշանակում, որ նրանք ավելի շատ թվեր չգիտեն: Ասենք, կարող են չորս թիվը նշանակել «երեք ու մեկ» տեսքով):  

Գրեթե բոլոր դեպքերում առաջին տասը թվերի համար գոյություն ունեն հատուկ անուններ՝ մեկ, երկու, երեք, չորս, հինգ, վեց, յոթ, ութ, ինը և տասը:

Կարելի էր շարունակել, տասից մեծ թվերի համար էլ անուններ հնարել, բայց դա լուրջ դժվարություններ կստեղծեր: Հեշտ չէր լինի «քառասուներեք», «յոթանասունինը» և մինչև անվերջություն թվերի հատուկ անունները հիշելը: Մյուս կողմից, մեկից տասը թվերի անունները հիշելը հեշտ է, քանի որ մեր ձեռքերին տասը մատ ունենք. դա հիշողության յուրօրինակ համակարգ է:

Մարդն ասում էր «չորս» և ցույց էր տալիս չորս մատ, ասում էր «վեց» և ցույց էր տալիս վեց մատ: Դիմացինը տեսնում էր մատները և հեշտությամբ հասկանում էր, թե ինչ նկատի ունի խոսակիցը, նույնիսկ եթե մոռացել էր, ինչ էին նշանակում «չորս» և «վեց» բառերը:

«Մատ» բառը լատիներեն «digitus» է, և  պատահական չէ, որ անգլերենում, որտեղ այդ բառը փոխառվել է լատիներենից, նոր նշանակություն է ստացել: «Digit»-ը անգլերեն նշանակում է թվանշան: Միանգամայն տրամաբանական է նաև, որ բոլոր առաջին տասը թվերին անվանում են թվանշան, այսինքն «digits», քանի որ հնում այն երկու հասկացությունները՝ մատներ և թվեր, փաստորեն նույնական էին:

Կարող է թվալ, որ գոյություն ունեն  տասից ավելի մեծ թվերի առանձին անուններ, բայց այդպես չէ: Ժամանակի հետ լեզուն վերափոխվում է, որոշ բառեր փոխարինվում են ուրիշներով, և այդ ժամանակ բառը երբեմն կորցնում է իր սկզբնական նշանակությունը: Ի՞նչ է նշանակում «տասնմեկ» բառը: Դա «տասը» և «մեկն»-է: Անգլերեն «տասնմեկը» «eleven»-է: Այդ բառն անգլերենում հայտնվել է հին գերմաներենից, որտեղ նշանակում էր «մեկով ավելի»:

Դժվար չէ այսպիսի մի պատկեր երևակայել: Մի մարդ մյուսին տասը մատն է ցույց տալիս և ավելացնում. «էլի մեկը»:

Հենց այդպես էլ ձևավորվել է «տասներկու» բառը, այսինքն «տասը» և «երկուս», «տասներեք», և այդպես մինչև քսան[1], այսինքն «երկու տասնյակ»: Անգլերենում էլ ամեն ինչ նույնն է: Տասներկուս` «twelve», նշանակում է  «երկուսով ավելի», այսինքն` տասից հետո երկու:

Տասներկուսից հետո ամեն ինչ հեշտանում է: Thirteen, տասներեքը «երեք և տասն» է, fourteen տասնչորսը`  «չորս և տասը», այդպես մինչև քսան: Քսան, twenty`ուղղակի «երկու տասնյակ», thirty`«երեք տասնյակ», forty`«չորս տասնյակ», այդպես մինչև հարյուր:

Ռուսերենում բացառություն է միայն «сорок» բառը: Ինչո՞ւ ենք ասում «сорок», ոչ թե «четыредесят»` «չորս տասնյակ»: Բանն այն է, որ հնում ռուսները հաշվել են «соро­к»-ներով[2], այդ պատճառով չորս տասնյակի համար հատուկ բառ են հնարել: Ասում էին, որ Մոսկվան «քառասուն քառասուն եկեղեցիների» քաղաք է, այսինքն Մոսկվան 40 х 40 կամ 1600 եկեղեցի ուներ: Այդ ժամանակներում հաշվի համար ոչ միայն դրամ են օգտագործել, այլ նաև սամույրի մորթի: Քառասուն մորթին մեկ մուշտակ էր, այսինքն` քառասուն թիվը նույնպիսի սահմանային թիվ էր, ինչպես տասը, հարյուրը, հազարը և այլն:

Թվի նշանակումը մատներով

Կարելի՞ է մատներն օգտագործել տասից ավելի մեծ թվեր նշանակելու համար: Օրինակ, ինչպե՞ս մատներով ցույց տաք 54 թիվը: Մի օր մի երիտասարդի տեսա, որ իր ընկերոջն սկզբում հինգ անգամ արագ-արագ ցույց տվեց ափերը բաց մատներով, հետո չորս մատ, այսինքն` սկզբում հինգ տասնյակ, հետո չորս, ընդամենը՝ 54: Այս ամենը հիանալի է, բացառությամբ նրա, որ դիտորդը պետք է զգոն լինի, որպեսզի մեկ կամ մի քանի տասնյակ բաց չթողնի: Նման դեպքերում սովորաբար հարցնում են «հիսունչո՞րս»: Իսկ դա ինչ է նշանակում, որ մատներով թվերը ցույց տալն անօգուտ էր: Իհարկե, մենք ստիպված չենք մատներով հաշվելու հմտություններ զարգացնել, դպրոցում թվերը բոլորովին այլ մեթոդներով ենք սովորում, և դրանք ավելի արդյունավետ են: Բայց եթե ստպված լինեինք մատներով հաշվել, օրինակ, կարող էինք պայմանավորվել հաշվի հետևյալ կարգը: Երբ  ձեռքի ափը պահում ենք դեպի ներս,  բացված մատները տասնյակ են նշանակում: Երբ ափերը դեպի դուրս են,  մատների քանակը ցույց է տալիս միավորները: Այդ ժամանակ նույն 54 թիվը մատներով կարելի է հետևյալ կերպ ցույց տալ: Մի ձեռքի ափը պահեք դեպի ներս, ցույց տալով հինգ մատ, իսկ մյուսը՝ ափով դեպի դուրս, ցույց տալով չորս մատ: Այդպիսով, երկու շարժումով կարելի է 10-ից 99 ցանկացած թիվ ցույց տալ:

Ահա և հասանք տասը տասնյակին, այսինքն` հարյուրին: «Հարյուր» բառը նույնպես հնուց է եկել: Ձեռքի ափերը դեպի ներս դարձնելով և տաս մատը ցույց տալով, կարող ենք նույնիսկ տաս տասնյակ ցույց տալ:

Իսկ ի՞նչ անենք, երբ անհրաժեշտ է տասնմեկ տասնյակ ցույց տալ: Դա նույնպես հնարավոր է:

Հասնելով հարյուրին, շարունակում ենք նույնությամբ գործել: Հարյուրին հաջորդող թիվը «հարյուր և մեկ»-ն է, այսինքն` հարյուր մեկը: Ի՞նչը կարող է ավելի պարզ ու հեշտ լինել: Շարունակում ենք առաջ ընթանալ, անցնում ենք տարբեր թվեր, որոնց անունները ձևավորվում են նույնպիսի պարզ սխեմայով, օրինակ` «հարյուր և քսաներեք» դա «հարյուր քսաներեք»-ն է, «հարյուր և յոթանասունինը» «հարյուր յոթանասունինն»-ն է, այդպես մինչև «հարյուր և իննսունինը», այսինքն «հարյուր իննսունինը»: Այժմ երկու հարյուրյակ ունենք, այսինքն` երկու հարյուր: Այս եղանակով կարող ենք հասնել մինչև «ինը հարյուրյակի և իննսունիննի», այսինքն` «ինը հարյուր իննսունինին»: Այստեղ հարմար է «տասը հարյուրյակ» թվի համար սկզբունքորեն նոր անուն ներմուծել: Այդ թիվը ստացավ «հազար» անունը. նրա ծագումը նույնպես դարերի խորքն է գնում:

Այժմ կարելի է նորից թվերը մատներով «գրելու»  նույն սկզբունքն օգտագործել և շարժվել առաջ:

Կարող ենք, օրինակ, պայմանավորվել, որ երբ մատները ներքև են ուղղված, իսկ ձեռքի ափը դեպի դուրս, ապա մատների քանակը հազարների քանակ է ցույց տալիս, իսկ երբ մատները ներքև են, ձեռքի ափը ներս, ապա՝ հարյուրների: Երբ մատները դեպի վերև են,  ձեռքի ափը՝ դուրս, ապա մատների քանակը տասնյակներ է նշանակում: Եվ վերջապես, երբ մատները դեպի վերև են, ձեռքի ափը՝ ներս, ապա մատների քանակը միավորների քանակն է ցույց տալիս:

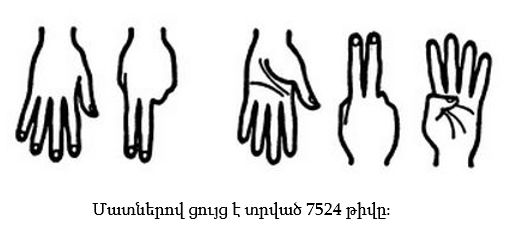
Ուստի, եթե ուզում ենք մատներով ցույց տալ «յոթ հազար հինգ հարյուր քսանչորս», կարող ենք չորս շարժումով անել. «յոթ մատ ներքև՝ ափով ներս, հետո հինգ մատ ներքև՝ ափով դուրս, երկու մատ վերև՝ ափը ներս, հետո չորս մատ վերև՝ ափը դուրս»:

Կենցաղում հազարից բարձր թվեր համարյա չենք օգտագործում, դրա համար էլ «տասը հազար», «քսան հազար» և այլ թվերի համար նոր անուններ անհրաժեշտ չէին ո´չ ռուսերենում, ո´չ  անգլերենում և ո´չ էլ եվրոպական շատ լեզուներում: «Տասը հազար»-ից հետո «տասը հազար մեկ»-ն է գալիս և  այդպես մինչև «տասը հազար ինը հարյուր իննսունինը», իսկ հետո` «տասնմեկ հազար»... «տասներկու հազար»... «հարյուր հազար» և այլն:

Հույն մաթեմատիկոսները տասը հազար թվի համար հատուկ անուն էին օգտագործում: Նրանք այդ թիվը  «տուպավ»[3] էին անվանում (նրանից է սկիզբ առել «անթիվ» կամ «անհամար» ժամանակակից բառը), բայց այդ թիվն օգտագործվում էր միայն գիտնականների նեղ շրջանակում և երբեք  լայն կիրառություն չի ունեցել: Այնպիսի թվերի համար, ինչպիսիք են  «միլիոն»-ն ու «միլիարդ»-ը, միայն ուշ Միջնադարում են անուններ հայտնվել, իսկ մարդկության պատմության մեծ մասում բավարար է եղել միայն երկու ձեռքի ափն ու տասը մատը, որպեսզի անհրաժեշտ թիվը ցույց տան:

Համրիչ

Ամենևին չեմ պնդում, որ մեծ թվերը մատներով արտահայտելու իմ համակարգը երբևէ օգտագործվել է: Այն ժամանակ, երբ սկսեցին կիրառվել տասնյակները, հարյուրյակները, հազարյակներն ու տասը հազարյակները, մարդկությունն արդեն հաշվումների համար յուրատեսակ արհեստական մատներով հարմարավետ գործիքի էր տիրապետում:  Դա համրիչն էր կամ հուներեն՝ «աբակը»:

Ամենահասարակ համրիչը հորիզոնական ակոսներով տուփ էր, որոնցից յուրաքանչյուրում տասը կլոր քար կամ ճալաքար կար: Ակոսների երկարությունը բավարար էր, որպեսզի  քարերն աջից ձախ շարժվեին:

Այդպիսի համրիչներից Հին Հունաստանում, Հին Հռոմում օգտվում էին և ավելի ուշ ժամանակներում: «Գետաքար»-ը լատիներեն «calculus» է, որից ծագել է «calculate» բառը, ինչ անգլերեն նշանակում է  «հաշվել»:

Հետագայում հայտնվեցին ուրիշ ձևի համրիչներ: Դա հորիզոնական ձողերով փայտե շրջանակ էր, որի վրա տասը սկավառակ էր հագցված, դրանց «հատիկ» էին անվանում: Ձողը բավական երկար է, որ «հատիկներ» կարողանան տեղշարժվել: Սկզբունքորեն յուրաքանչյուր ձողը  տասը մատներով ափի մոդելն է:

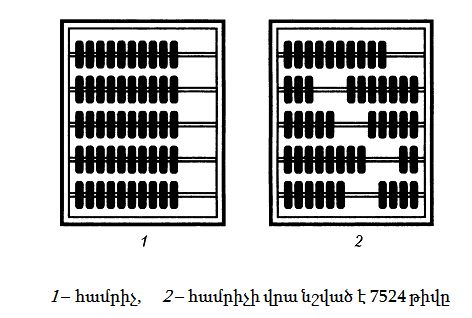
Եթե սկզբում բոլոր հատիկները ձախ կողմում են, մեկ հատիկ շարժելով դեպի աջ,  նմանակում ենք մեկ մատ բարձրացնելու ժեստին: Իսկ հիմա պայմանավորվենք, որ հատիկների ներքևի շարքը միավորներն են, նրանից վերև՝տասնյակները: Ավելի վերև՝ հարյուրյակները, իսկ հարյուրյակներից վերև՝ հազարյակները: Այժմ 7524 թիվը փորձենք պատկերացնել համրիչով: Ստորին շարքում անհրաժեշտ է 4 հատիկ տեղաշարժել, հաջորդում՝ 2, հաջորդում՝ 5, վերջապես, ավելի վերևում՝ 7:

Հասկանալի է, որ ավելի հարմար է օգտվել համրիչից, քան թվերը մատներով ցույց տալ: Համրիչը մի քանիս առավելություն ունի, և դրանք բավականին լուրջ են:  Նախ, ինչ-որ թիվ ցույց տալու համար պետք չէ հիշողությունը քչփորել, թե ինչպես դասավորես մատներն ու ձեռքի ափը: Երկրորդ՝ կարող ես ամբողջ թիվը ոչ թե մաս-մաս, այլ միանգամից ամբողջը ցույց տալ, նույնիսկ եթե դա տասը կամ հարյուր հազար է: Կարիք չկա հիշելու, թե քանի հազարյակ, հարյուրյակ և տասնյակ կար: Երրորդ՝ երբ օգտվում ես համրիչից, կարող ես ինչքան ասես շարք ավելացնել, այդպիսով սկզբունքորեն ցուցադրելով կամայական մեծ թիվ: Եվ վերջապես, համրիչները միաժամանակ երկու թիվ ցույց տալու և դրանց հետ ինչ-որ գործողություն կատարելու հնարավորություն են տալիս:

Հաշվում ենք համրիչով

Մարդուն դեռևս նախապատմական ժամանակներում անհրաժեշտ էր թվերը գումարել և հանել: Ենթադրենք, որ դուք հարևանից նետի մի քանի սլաք եք ձեռք բերել, և անհրաժեշտ է իմանալ, թե այժմ քանի ծայրակալ ունեք:

Կամ էլ, ասենք, ձեր ոչխարները մի քանի գառ են ունեցել, դուք պետք է իմանաք, թե ավելացումից հետո քանի գլուխ ոչխար դարձավ ձեր հոտը:

Ամենապարզ ձևը հաշվելն է: Ենթադրենք` ունեք հինգ սլաք և ձեռք եք բերել ևս երկուսը: Դրանք դնում եք միասին և հաշվում եք, ստացվում է՝ յոթ: Կամաց-կամաց հաշվելու հմտություն է ձևավորվում, և արդեն իմանում եք, որ հինգ գումարած երկու հավասար է յոթ:

Բայց մեր հիշողությունն անսահման չէ, և երբ անհրաժեշտ է մեծ թվեր գումարել, օրինակ` քսաներեք և հիսունչորս, պատասխանը գտնելն ավելի դժվար է: Պատկերացրեք հին ժամանակների հովվի, որի հոտում հիսունչորս ոչխար կար, իսկ հետո ավելացավ ևս քսաներեքը: Ահա նա երկար-բարակ հաշվում է, շփոթվում, նորից սկսում, էլի շփոթվում... և սեփական անճարությունից կատաղում է: Թերևս, ավելի լավ է այս մեթոդով հաշվող մարդուց հեռու մնաք:

Ահա այստեղ կարող է օգնության գալ համրիչը: Դա շատ հարմար սարք է, որն օգնում է հաշվել այդ երկու թվերի գումարը՝ առանց հատուկ մտավոր ջանքերի: Հիմա ընդհանրապես կարիք չկա այդ հիմար ոչխարների կողքին լինելու, որ չեն կարողանում տեղում կանգնել և անընդհատ դես ու դեն են փախչում: Կարելի է տուն գնալ և այնտեղ հաշվել: Եթե պետք է հիսունչորսին քսաներեք գումարել, ապա հաշվիչի ներքևի, այսինքն` միավորի շարքում, տեղափոխում ենք չորս հատիկ: Հաջորդ՝ տասնյակների շարքում՝ հինգ: Հիմա ներքևի շաքում ավելացնում ենք ևս երեքը, իսկ հաջորդին՝ երկուսը: Արդյունքում  յոթանասունյոթ ենք ստանում: Ճիշտ է, հաշվելիս գումարը ոչ մի անգամ տասը կամ ավելի մեծ թիվ չստացվեց:

Ճիշտ նույն ձևով, առանց ավելորդ հարցերի, կարելի է ավելի մեծ թվեր գումարել: Օրինակ` պետք է գումարել երկու հարյուր հիսուներեք հազար հարյուր տասներկուս և հարյուր քսանվեց հազար ութ հարյուր երեսունմեկ թվերը: Համրիչ օգտագործելով, կարող ենք  հեշությամբ որոշել գումարը, որը հավասար է երեք հարյուր յոթանասունինը հազար ինն հարյուր քառասուն երեքի: Բայց այդ հեշտությունը մասամբ գալիս էր նրանից, որ գումարելիս ոչ մի շարքում տասից մեծ թիվ չստացանք:

Իսկ հիմա պատկերացրեք, որ պետք է համրիչով գումարել յոթ և ութ թվերը: Որքան էլ տարօրինակ է, դա ավելի բարդ է, քան մի քանի հարյուր հազարների գումարը հաշվելը, ինչ նոր արեցինք:

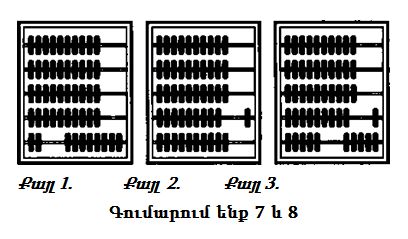Նայեք նկարին:

Սկզբում ներքևի շարքում ութ հատիկ աջ եք տեղափոխում: Այժմ պետք է դրանց ավելացնել ևս յոթը, բայց մեզ անհրաժեշտ շարքում միայն երկու ազատ հատիկ կա:

Ի՞նչ անենք: Ամեն ինչ շատ պարզ է: Սկզբում տեղափոխեք մնացած երկուսը: Այժմ ամբողջ տասնյակ ունեք: Փոխարինում եք կատարում. այդ շարքի տասը հատիկները փոխարինում եք հաջորդ շարքի մեկ հատիկով, այսինքն` տասնյակների շարքում գցում ենք մեկ հատիկ: Արդեն կարող եք ավարտել գումարումը, քանի որ միավորների շարքը ազատ է: Պետք էր յոթ հատիկ տեղափոխել: Երկուսն արդեն տեղափոխել էինք: Այսինքն, մնացել է հինգը: Ներքևի շարքից հինգ հատիկ տեղափոխում ենք աջ և ստանում ենք արդյունքը` մեկ տասնյակ և հինգ միավոր, այսինքն` տասնհինգ:

Տասը հատիկի այսպիսի փոխարինումը վերևի շարքի մեկ հատիկով հարմար է բոլոր շարքերի համար: Տասը տասնյակը կարելի է փոխարինել մեկ հարյուրյակով, տասը հարյուրյակը՝մեկ հազարյակով և այլն:

Այդպիսով, երբ համրիչ ենք օգտագործում, տասից ավելի հատիկ հաշվելու անհրաժեշտություն չկա: Իրականում բավարար է մինչև հինգը հաշվելը: Չէ՞ որ եթե աջ եք տարել հինգ հատիկից ավելի, պետք  կլինի միայն հաշվել ձախ կողմի հատիկների քանակը (դրանք հինգից քիչ են լինելու), որպեսզի իմանաք, թե քանիսն են աջ կողմում: Ասենք, եթե ձախ կողմում մնացել է մեկ հատիկ, նշանակում է, որ աջում ինն է:

Երբ հատիկները հինգն են կամ քիչ, մեզ  համար հեշտ է, առանց հաշվելու, առաջին հայացքից տարբերել դրանց քանակը: Այդ պատճառով էլ փորձառու աշխատողը, որ անընդհատ համրիչով է հաշվում, կարող է գումարման կամ հանման գործողությունը մեծ արագությամբ կատարել, ավելի արագ, քան դա արվում է սովորական մեթոդով՝ թղթի վրա, սյունակային եղանակով: Համրիչով  աշխատող ամենահայտնի մասնագետներին հաջողվել է գերազանցել նույնիսկ սեղանի էլեկտրական հաշվիչ մեքենաներին:

Համրիչ օգտագործելով, կարող եք հեշտությամբ ցույց տալ, որ գումարելիների տեղափոխությունից գումարը չի փոխվում: Կարևոր չէ, թե որ թիվն եք առաջինը գցել համրիչի վրա: Կարող եք սկզբում գցել յոթը, հետո` ութը, կամ հակառակը, արդյունքը նույնն է մնում՝ տասնհինգ:  Այնպես, որ այս կանոնը լավ հիշեք՝ գումարելիների տեղերը փոխելիս գումարը չի փոխվում:

Թվերը պատկերում ենք տառերի միջոցով

Այսպիսով, պարզեցինք, թե համրիչն ինչ օգտակար և հարմար գործիք է: Բայց հաշվարկման արդյունքները պետք է ինչ-որ ձևով գրանցել: Ե´վ հին Բաբելոնում, և´ Հին Եգիպտոսում կանոնավոր կերպով գրանցում էին տիրակալների գանձարան մուտք արվող հարկերը, տուրքերը, պաշարները և  շատ ուրիշ բաներ: Կարելի է, իհարկե, թվերը բառերով գրանցել, ինչպես դա արվել  է գլխի սկզբում, օրինակ`  երկու հարյուր հիսուներեք հազար հարյուր տասներկու: Այդպիսի գրառումը կարելի է ցանկացած լեզվով անել, բայց դա բավական հոգնեցնող է և անհարմար: Եվ օգնության եկան հապավումներն ու նշագրումները:
Արդեն հին ժամանակներում դպիրները թվերը գրելու համար նշաններ, սիմվոլներ և այբուբենի տառեր էին օգտագործում: Կքննարկենք թվերը տառերով պատկերելու համակարգը, որն օգտագործել են հին հռոմեացիները: Այն մինչև հիմա էլ օգտագործվում է: Հռոմեական թվանշանները կարող ենք տեսնել հուշարձանների, հանրային շինությունների, ժամացույցների, դիպլոմների և պատվոգրերի վրա, այնպես որ դրանք մեզ շատ լավ ծանոթ են:

Մեկ թիվը հռոմեական համակարգում նշանակվում  է I, երկուսը՝  II, երեքը՝  III, չորսը՝  IIII, հինգը՝ V (հնարավոր է, սա ձեռքի ափի թեքումը դեպի բթամատ սխեմատիկ պատկերն է), վեցը՝  VI, յոթը՝  VII, ութը՝  VIII, ինը՝ VIIII, տասը՝  X (հնարավոր է, այս նշանը պատկերում է երկու ափերի դեպի բթամատ թեքումը, մեկը՝ մատներով վերև, մյուսը՝ ներքև): Հետո գալիս է հիսունը` L, հարյուրը` С, հինգ հարյուրը` D, հազարը`М . Այսպես հազար ինը հարյուր հիսունութ թիվը հռոմեական թվագրության համակարգում այս տեսքը կունենա MDССССLVШ (այսինքն` մեկ հազար + հինգ հարյուր + հարյուր + հարյուր + հարյուր + հարյուր + հիսուն + հինգ + մեկ + մեկ + մեկ):
Ուշադրություն դարձրեք, որ հռոմեական թվագրության համակարգում հատուկ սիմվոլները, անկախ իր զբաղեցրած տեղից, միշտ նույն թիվն են նշանակում:

Ասենք, МБССССЬУШ փոխարեն կարելի է գրել  СLСDIIVСМСI, և դա նույն թիվը կլինի: Միակ պատճառը, որը ստիպեց դպիրներին աջից ձախ նվազման կարգով դասավորել սիմվոլները, թիվը կարդալու հարմարավետությունն էր: Մոտավորապես այնպես, ինչպես բրիջ խաղի ժամանակ, խաղաքարտի նշանակությունը միշտ նույնն է մնում, բայց խաղացողները դասավորում են դրանք աջից ձախ՝ նվազման կարգով:

Մեր օրերում ուսուցման մի փոքր փոփոխված համակարգ են օգտագործում:

Փոքր թիվ արտահայտող նշանը դնում են մեծի առջև, երբ այն պետք է մեծից հանել: Օրինակ, մենք սովորել ենք չորս թիվը գրել IV, և ոչ թե՝ IIII, իսկ ինը հարյուրը՝ СМ, և ոչ թե՝ DСССС: Հին հռոմեական թվագրության համակարգի այս կատարելագործումը ներմուծվել է արդեն միջնադարում՝ գրությունը կրճատելու նպատակով, և հին հռոմեացիները դրանից չեն օգտվել:

Այսպիսով, հռոմեական թվագրության համակարգում սիմվոլի նշանակությունը կախված չէր նրա դիրքից, այսինքն` այդ համակարգը տարբերվում էր համրիչով նշագրման համակարգից, որտեղ թվի նշանակությունը կախված էր, թե որ շարքում է այն գտնվում:

Այնուամենայնիվ,  հռոմեական թվագրման համակարգում էլ կարելի է գումարման գործողություն կատարել: Օրինակ, մեզ անհրաժեշտ է գումարել  МDССССLVШ և ММССССLХХII թվերը: Գրենք նոր թիվը` նշելով երկու թվերի թվանշանները միասին:
Կստանանք.МММDССССССССLLХХVIIШ:

Այժմ պարզեցնենք այս արտահայտությունը:

Հինգ միավորը կամ ШII-ը V է, երկու հատ հիսունը (LL)` հարյուր (С).

Փոփոխարինում կատարով՝  ստացվում է МММDСССССССССХХVV:

Բայց երկու հինգը (VV) կլինի տասը, հինգ հատ հարյուրը (ССССС)` հինգ հարյուր (D):

Եվս մի փոփոխություն  կատարելով հետևյալ արդյունքը կստանանք` МММDDССССХХХ.

Բայց երկու հատ հինգ հարյուրը կանի հազար (М). վերջին հնարավոր փոփոխությունը կատարենք և կստանանք վերջնական արդյունքը` ММММССССХХХ, այսինքն չորս հազար չորս հարյուր երեսուն:

Մի´ կասկածեք, որ Հին Հռոմում փորձառու դպիրը կայծակնային արագությամբ կարող էր այս գործողությունը կատարել: Բայց կան ուրիշ, թվային շատ անհրաժեշտ գործողություններ, որոնք հեշտ է համրիչով կատարել և դժվար՝ հռոմեական թվանշաններ օգտագործելով: Հենց թվերը գրելու ռացիոնալ համակարգի բացակայությունը կանգնեցրեց մաթեմատիկայի զարգացումը Հին Հունաստանում, քանի որ հույները թվերը գրում էին ոչ պակաս դժվար և անհարմար եղանակով, քան հռոմեացիները: Եթե հնադարի ամենամեծ մաթեմատիկոս Արքիմեդը տիրապետեր ժամանակակից թվագրության համակարգին, նա կկարողանար Նյուտոնից շատ առաջ հանգել դիֆերենցիալ հաշվի գաղափարին, ինչը տասնութ դարով կարագացներ գիտության զարգացումը: Մեր թվարկության  IX դարում մի հնդիկ, ում անունը չի պահպանվել, մշակեց  այն հաշվարկման համակարգը, որը մինչև հիմա օգտագործվում է:

Հնդկաստանից այդ համակարգը տարածվեց  արաբական արևելք, իսկ արաբներն էլ բերեցին Եվրոպա: Դրա համար էլ մեր թվանշաններն անվանում են արաբական, չնայած ճիշտ կլիներ այն հնդկական անվանելը: Հնդկական համակարգը ուղղակի մոդելավորեց թվերի պատկերումը համրիչի միջոցով. դրա մասին` մի փոքր ուշ: Անհասկանալի է, թե ինչու այդ հայտնագործությունն այդքան երկար սպասել տվեց, չէ՞ որ համրիչներն արաբական թվերից շատ վաղ էին հայտնագործել:

Շարունակությունը

Թարգմանություն ռուսերենից
Լուսանկարը`fantlab.ru-ից