Թվային բուրգից մինչև գունավոր գորգ

Երկար տարիներ աշխատելով կրտսեր դպրոցում, շփվելով հիմնականում մինչև 10, 11 տարեկան երեխաների հետ, դասավանդողը, չկիրառելով` կարող է մոռանալ մաթեմատիկայից որոշ թեմաներ: Դրանից զերծ մնալու համար (Գևորգ Հակոբյանի խորհրդով) որոշեցինք մաթեմատիկայի որոշ թեմաներ պարզեցնել, փոփոխել այնքան, որ հասանելի լինի անգամ կրտսեր դպրոցի սովորողին, միևնույն ժամանակ սովորողին հնարավորություն տալով զբաղվելու մաթեմատիկայով՝ խնդիրներով, որոնք լուծելու համար պահանջվում է երկար ժամանակ (մի քանի պարապմունք), փորձարարությամբ, զարգացնելով ուշադրություն, դիտողականություն, աշխատանքի ճշտակատարություն, ցրելով պատկերացումը, թե մաթեմատիկոսները թափթփված ժողովուրդ են: Կարևոր է նաև առաջին հայացքից իրար հետ կապ չունեցող թեմաներն իրար կապելը:

Նախկինում էլ այդպիսի փորձեր մի քանի անգամ արել եմ, և այդ պարապմունքները առավել հետաքրքիր և արդյունավետ են անցել: Որպես աշխատանքային թեմա` ընտրեցինք Պասկալի եռանկյունը:

Ընթացքը: Աշխատել ենք մաթեմատիկայի ընտրությամբ դասերին, 4-5-րդ դասարանցիների հետ:

Նախնական փուլ: Սկսեցինք օրինաչափություն թեմայից. սովորողների հետ մի քանի պարզ օրինակներ վերհիշեցինք ամենամսյա մաթեմատիկական ֆլեշմոբից (հաճախ են հանդիպում այդպիսի խնդիրներ, որոնք, կարգի համաձայն, հետո դասարանում քննարկում ենք), ինչպես նաև ընտրված նոր խնդիրներ առաջարկեցինք: Սովորողներն էլ հնարավորություն ունեցան իրնց ստեղծած նմանապտիպ խնդիրները առաջարկելու:

Առաջին քայլ: Իրար ետևից նկարիր 10 քառակուսի (այստեղ սովորողները մեկ անգամ ևս վերհիշում են word ծրագրի գործիքները, կային սովորողներ, ովքեր համառորեն աշխատում էին paint ծրագրով), ընտրիր երկու գույն: Գունավորի'ր քառակուսիները այնպես, որ հարևան (իրար կպած) քառակուսիները լինեն տարբեր գույնի:

Օրինակ`

Երկրորդ քայլ: Իրար ետևից նկարիր 10 քառակուսի, փորձիր գունավորել հետևյալ կանոնով: Առաջին երկու քառակուսիները գունավորիր կապույտ, իսկ մնացած քառակուսիները ներկելու համար նայիր նախորդ երկու քառակուսիների գույնին.

ա) եթե ներկված են նույն գույնով, հաջորդը կարմիր ներկիր:
բ) եթե ներկված են տարբեր գույներով, հաջորդը կապույտ ներկիր:

Տես`

Այստեղ այն սովորողները, ովքեր ավելի արագ էին նկարում, շտապեցին շարքը շարունակել և հետաքրքիր եզրահանգումներ արեցին, ինչպես`

• եթե քառակուսիները համարակալենք, երեքի պատիկ տեղերում քառակուսին միշտ կարմիր կլինի,
• եթե շարքում վանդակների թիվը երեքի պատիկ է, ապա առաջին և վերջին վանդակների գույները տարբեր կլինեն, իսկ մնացած դեպքերում կլինի կապույտ (5-րդ դասարանցի Կարինե Գոմցյանի եզրահանգումը):

Երրորդ քայլ: Ստեղծագործական փուլ: Իրար ետևից նկարիր քառակուսիներ (10-ից շատ): Ընտրի'ր տարբեր գույներ, փորձիր ինչ-որ կանոնով գունավորել քառակուսիները և կանոնը բառերով ձևակերպել:

Այս փուլը, թերևս, ամենահետաքրքրին էր ինձ համար. բոլոր սովորողները (28 սովորող) տարբեր գույներ ընտրեցին և ունեցանք շատ տարբեր լուծումներ, տարբեր պատկերներ: Հետաքրքիր էր չորրորդ դասարանի սովորող Յանայի կանոնը՝ քառակուսիների գույները փոխվում են ծիածանի յոթ գույների նման՝ նույն հերթականությամբ. իր կանոնը կիրառելու համար Յանան երկարացրել էր քառակուսիների շարքը:

Չորրորդ  քայլ: Իրար ետևից նկարիր 10 քառակուսի, առաջին երկու քառակուսիներում գրիր 1 թիվը, երրորդից սկսծ՝ յուրաքանչյուր քառակուսում գրիր նախորդ երկու քառակուսիներում գրված թվերի գումարը:

Գունավորիր զույգ թվերը կարմիր, իսկ կենտ թվերը` կապույտ։

Այստեղ ևս սովորողները, նայելով թվերին, գույներին, եկան հետևյալ եզրակացության`

• երկու կենտ թվերի գումարը միշտ զույգ է,
• կենտ և զույգ թվերի գումարը կենտ է:

Հինգերորդ  քայլ: Այս փուլում փորձեցինք փոխել քառակուսիների դիրքը, դրանք դասավորեցինք բուրգի նման: Տես նկարը։

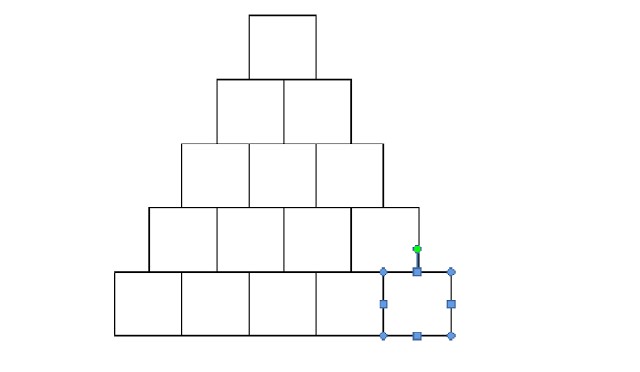
Առաջադրանքներ

1. Շարունակի'ր քառակուսիներով տողերը լրացնել այնքան, որ վերջին տողում լինի 20-ից ոչ պակաս քառակուսի:

2.Վերցրու երկու գույն` կապույտ և կարմիր, ներկիր քառակուսիներով պատրաստած բուրգը հետևյալ կանոնով`
ա) ամենավերևի քառակուսին կապույտ ներկիր,
բ) յուրաքանչյուր տողի առաջին և վերջին քառակուսիները կապույտ ներկիր,
գ) մնացած քառակուսիները ներկելու համար նայիր այդ քառակուսու անմիջապես վերևում տեղադրված երկու քառակուսիների գույնին.

• եթե նույնն են` կարմիր ներկիր,
• եթե տարբեր են` կապույտ:

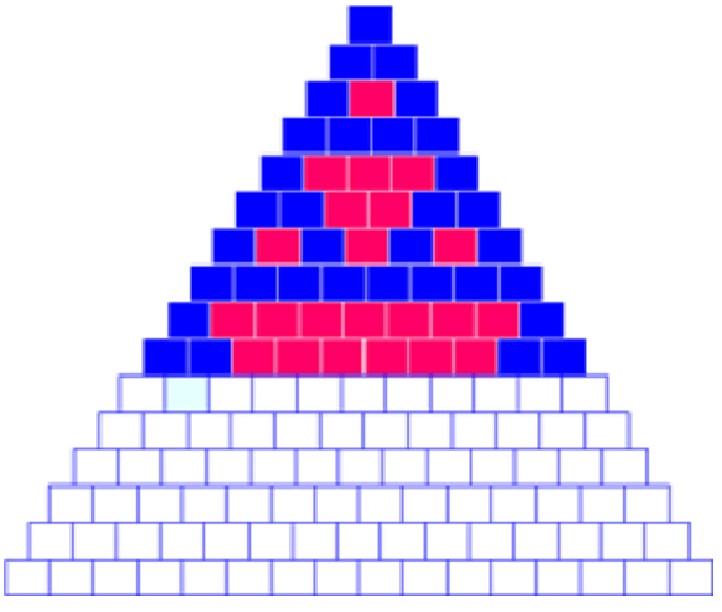
Վեցերորդ  քայլ: Աշխատանքը բոլորն էլ մեծ ոգևորությամբ էին կատարում, քանի որ գույները բուրգը գեղեցիկ նախշերով էին լցնում, դարձնում նախշազարդ գորգ լիներ:

Ուսումնասիրում ենք ստացած գունավոր բուրգը:
Փորձենք գունավոր բուրգը դարձնել թվային.

ա) ամենավերևի քառակուսում 1 գրիր.
բ) յուրաքանչյուր տողի առաջին և վերջին քառակուսիներում գրիր 1.
գ) մնացած քառակուսիներում թվերը գրելու համար, հաշվիր, այդ քառակուսու անմիջապես վերևում տեղադրված երկու քառակուսիների թվերի գումարը.
դ ) կառուցիր թվային բուրգը այնպես, որ վերջին տողում քառակուսիների թիվը լինի 16-ից ոչ պակաս:

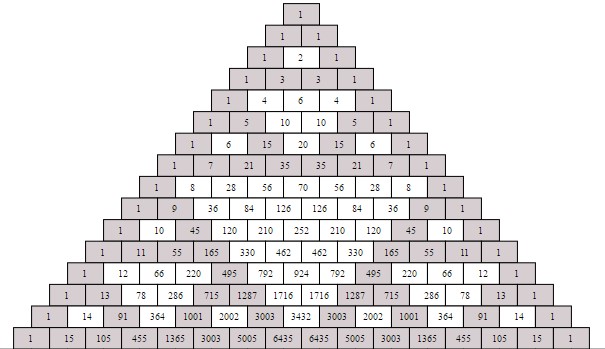
Յոթերորդ  քայլ։ Եզրահանգման փուլ:

Մառա Մկրտչյանն առաջինն էր, որ աշխատանքը ավարտեց, և մի քանի եզրակացություն արեց`

• սպիտակ եռանկյան մեջ գրված բոլոր թվերը զույգ են:
• յուրաքանչյուր տողի երկրորդ վանդակների կամ նախավերջին վանդակների թվերը իրար հաջորդող թվային շարք է,
• կա տող, որի բոլոր թվերը կենտ են.
• թվային բուրգն ունի համաչափության առանցք:

Եղան սովորողներ, ովքեր այդպես էլ դժվարացան բուրգը մինչև վերջ կառուցել (15 տող) և ըստ կանոնի այն դարձնել թվային:

Այստեղ կարևոր էր նաև այն, որ սովորողները կապ գտնեին թվային բուրգի որևէ տողի համարի և այդ տողում տեղադրված թվերի գումարի միջև, բայց այս փուլում, կարծում եմ, ե'ս էլ, տիար Գևո'րգն էլ (նշեմ, որ մաթեմատիկայի ընտրությամբ դասերը միասին ենք անցկացնում) մի քիչ շտապեցինք և ոչ մի սովորող չնկատեց, որ թվային բուրգի n-րդ տողի թվերի գումարը հավասար է 2^n-ի:

Այնուհետև դիտարկեցինք հետևյալ խնդիրները:

Խնդիր 1. Ունենք երեք աշակերտ` Արման, Ալեն, Սամվել:

ա) Քանի ՞ եղանակով է հնարավոր ընտրել մեկ հերթապահ:
Լուծում: Հնարավոր է երեք տարբերակով` Ալեն, Արման, Սամվել:
Պատասխան` 3:

բ) Քանի ՞ եղանակով է հնարավոր երկու սովորողի հերթապահ ընտրել:
Լուծում:
Արման, Ալեն
Արման, Սամվել
Ալեն, Սամվել
Պատասխան` 3:

գ) Քանի ՞ եղանակով է հնարավոր երեք սովորողի հերթապահ ընտրել:
Հնարավոր է մեկ դեպք` Արման, Սամվել, Ալեն:
Պատասխան`1:

Խնդիր 2. Ունենք չորս աշակերտ` Արման, Ալեն, Սամվել, Կարեն:

ա) Քանի ՞ եղանակով է հնարավոր ընտրել մեկին հերթապահ:
Լուծում։ Հնարավոր է չորս դեպք` Արման, Ալեն, Սամվել, Կարեն:
Պատասխան`4:

բ) Քանի ՞ եղանակով է հնարավոր ընտրել երկու սովորողի հերթապահ:
Լուծում: Արման, Ալեն,
Արման, Սամվել
Արման, Կարեն
Ալեն, Սամվել
Ալեն Կարեն
Սամվել, կարեն
Հնարավոր է 6 դեպք:
Պատասխան`6։

գ) Քանի՞ եղանակով է հնարավոր ընտրել երեք սովորողի հերթապահ:
Լուծում: Արման, Ալեն, Սամվել
Արման, Ալեն, Կարեն
Արման, Սամվել, Կարեն
Ալեն, Սամվել, Կարեն
Պատասխան`4

դ) Քանի ՞ եղանակով է հնարավոր ընտրել չորս սովորողի հերթապահ:
Լուծում։ Հնարավոր է մեկ դեպք` Արմեն, Ալեն, Սամվել, Կարեն:
Պատասխան` 1։

Խնդիր 3. Կառուցիր աղյուսակ 6x6 չափի: Փորձիր նախորդ երկու խնդիրների տվյալները և պատասխանները տեղավորել աղյուսակում հետևյալ ձևով`

Սովորողները աղյուսակում թվերը տեղադրելուց հետո միայն նկատեցին, որ այն համընկնում է իրենց կառուցած բուրգի տողերում գրված թվերի հետ և աղյուսակի հինգերոդ տողի թվերը (երբ հերթապահների թիվը հինգ սովորող է) դասավորեցին միանգամից, առանց խնդիրը լուծելու:

Ի՞նչն է զարմանալի. մենք վաղուց վերջացրել ենք այդ աշխատանքը, բայց 5-2 դասարանից Վահան Մանուչարյանը ասաց, որ պարապ ժամանակ դեռ շարունակում է թվային բուրգը մեծացնել, մինչև…