Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Սկիզբը 
Նախորդ հատվածը

Գլուխ 4. Կոտորակված թվեր

Բաժանում ենք միավորները

Մարդկությունը չէր կարող համաձայնել բաժանման սահմանափակումների հետ: Ենթադրենք, որ երկու խնձորը անհրաժեշտ է չորս երեխաների միջև բաժանել: Լրիվ անօգուտ է նրանց բացատրելը, որ այդպիսի բաժանում հնարավոր չէ, քանի որ չկա այնպիսի թիվ, որը 4-ով բազմապատկելիս 2 ստանանք: Եվ ոչ մի մայր այդպես չի անի: Նա պարզապես կկիսի յուրաքանչյուր խնձորն ու ամեն երեխայի կտա կես խնձոր (կամ այդ խնձորներից խյուս կպատրաստի):

Այս համակարգին հետևելով՝ մարդկությունն արդեն վաղուց է սովորել չափման հիմնական միավորները բաժանել ավելի փոքրերի և այդ նոր միավորներին սեփական անուններ տալ: Օրինակ, ծավալի չափման ամերիկյան համակարգում գոյություն ունի կվարտ անունով միավոր. եթե կվարտը կիսենք, կստանանք երկու նոր միավոր՝ փինտ: Եթե դուք ունեք երկու կվարտ գարեջուր, որը պետք է բաժանեք չորս մարդու, ապա յուրաքանչյուրը կստանա մեկական փինտ:

Կարելի է միավորը երկուսից մեծ թվերի էլ բաժանել: Օրինակ, բուշելը (ծավալի չափման ամերիկյան ևս մեկ միավոր) կարելի է բաժանել  4 պեկի, իսկ  պեկը՝ 8 կվարտի: Մեկ ֆունտը կարելի է բաժանել 16 ունցիայի, իսկ 1 կվարտը՝ 32 հեղուկ ունցիայի: Այս բոլոր թվերը ինչ-որ մեծություն կիսելու արդյունք են, ապա այդ մասերից յուրաքանչյուրը նորից են կիսել և այլն:

Կարելի է, օրինակ, մեկ կվարտը բաժանել երկու մարդկանց միջև, եթե յուրաքանչյուրին տանք 16 հեղուկ ունցիա (այսինքն՝ 1 փինտ): Իսկ եթե մեկ կվարտը պետք է բաժանել չորս մարդու միջև, ապա յուրաքանչյուրը կստանա 8 հեղուկ ունցիա (այսինքն՝ կես փինտ): Իսկ եթե 8 մարդ է, ապա յուրաքանչյուրին՝ 4 հեղուկ ունցիա (կամ 1 ջիլ):

Այս ամենը հիանալի է, բայց ի՞նչ անենք, եթե պետք է ինչ-որ բան երեքի բաժանել: Չենք կարող կվարտը, որը 32 ունցիա է պարունակում, բաժանել երեքի, քանի որ 32-ը 3-ի չի բաժանվում: Կվարտը հարմար է  բաժանել 16-ի կամ 32-ի:

Հետևաբար, օգտակար կլինի ընտրել ինչ-որ միավոր, որը հնարավորինս շատ թվով բազմապատիկ կունենա:

Այդ թվերից մեկը 12-ն է: Մեկ ֆութը 12 դյույմ է, տրոյական (ֆրանսիական Տրուա քաղաքի անունով) ֆունտը 12 տրոյական ունցիա է պարունակում, իսկ 12-ն, ինչպես հայտնի է, դյուժինն է:

Ուշադրություն դարձրեք դյուժինին, շատ օգտակար միավոր է: Եթե մի դյուժին խնձոր ունեք, կարող եք բաժանել երկու վեցյակի, երեք քառյակի, չորս եռյակի, վեց զույգի, տասներկու հատ մեկի: Շատ կարևոր է, որ 12-ը բաժանվում է ոչ միայն 2-ի և 4-ի, այլև 3-ի:

Դյուժինն առաջ օգտագործում էին առևտրի մեջ, քանի որ դյուժինը հեշտ է տարբեր եղանակներով բաժանել ավելի մանր մասերի: Գոյություն ուներ նաև միավոր, որը հավասար էր դյուժին դյուժինի (գրոս), որը հավասար էր 12х12 կամ 144. 144 թիվը ավելի շատ բազմապատիկներ ունի՝ 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48 և 72:

Այդպիսի համակարգը հարմար է և գործնական, այն հեշտ է օգտագործել առօրյա կյանքում, և կան մարդիկ, որ նույնիսկ ափսոսում են, որ մեր հաշվարկի համակարգի հիմքում 10-ն է, ոչ թե 12-ը: 10 թիվն ունի միայն երկու արտադրիչ՝ 2 և 5: Տասը չի բաժանվում ո՛չ 3-ի, ո՛չ էլ 4-ի: Համակարգի հիմքում 10 թվի հայտնվելու միակ պատճառը մեր յուրաքանչյուր ձեռքի 5 մատ ունենալն է: Այ, եթե վեց լիներ….

10 թիվը մի առավելություն ունի12-ի նկատմամբ: 10-ը բաժանվում է 5-ի, իսկ 12-ը՝ ոչ: Հին բաբելոնցիները փորձում էին մեկ թվի մեջ միավորել 10 և 12 թվերի բոլոր առավելությունները: Այդպիսի թիվը պետք է բաժանվի ոչ միայն 2-ի, 3-ի և  4-ի, այլև 5-ի: Այդպիսի ամենափոքր թիվը 60-ն է: Այս թիվն օգտագործվում է աստղագիտության մեջ: Տարին 365 օր և մի քանի ժամ է: Տարին այն ժամանակն է, որի ընթացքում Արեգակն ավարտում է իր (թվացյալ) շրջանաձև պտույտը երկնքում անշարժ աստղերի նկատմամբ: Եթե ամբողջ շրջանը բաժանենք ճանապարհի մեծությանը, որն անցնում է Արեգակը մեկ օրում (այսինքն «ճանապարհ-օր»-ում),  կստանանք շրջանի մեկ երեք հարյուր վաթսունհինգերորդ մասը:

Բաբելոնցիների տարին հավասար էր 360 օրվա (նրանք կա´մ ճիշտ չէին հաշվել տարվա տևողությունը, կա´մ ուղղակի 365 կլորացրել էին մինչև 360՝ հաշվարկները կատարելու հարմարության համար): Այս թվի հետ հեշտ է աշխատելը, քանի որ 360-ը 60х60-ն է: Դրա համար էլ նրանք երկնային ոլորտը և ուրիշ շրջաններ 360 հավասար մասերի են բաժանել, որոնց մեր օրերում անվանում ենք աստիճաններ: Այնուհետև յուրաքանչյուր աստիճանը բաժանգլ են 60 մասի, որոնք անվանում ենք րոպեներ, իսկ յուրաքանչյուր րոպեն` ևս 60 մասի՝ 60 վայրկյանի:

Մինչև հիմա էլ հետևում ենք բաբելոնյան համակարգին: Ավելին, քանի որ ժամանակը չափվում է երկնքում երկնային մեծ մարմինների շարժմամբ, մեր ժամը բաժանված 60 րոպեի, իսկ րոպեն՝ 60 վայրկյանի:

Ժամանակի հաշվելու դեպքում ևս 12-ական համակարգի հետքերի ենք հանդիպում: Գիշերն ու ցերեկը  բաժանված են 12 ժամի: Հնում, մինչև ժամացույցի գյուտը, ժամի տևողությունը փոփոխվում էր տարվա եղանակից կախված: Ձմռանը ցերեկվա ժամերը կարճ էին, քան ամռանը, իսկ գիշերայինները՝ երկար: Մեր օրերում ժամի տևողությունը հաստատուն է համարվում, դրա համար էլ ամռանը ցերակային ժամանակն ավելի երկար է, քան ձմռանը, գիշերայինը` հակառակը՝ կարճ:

Այնուամենայնիվ մեր ժամացույցների թվատախտակների վրա ընդամենը 12 թիվ կա, և, հետևաբար, մենք ժամանակըը որոշում ենք գիշերվա ժամը 1-ի և ցերեկվա ժամը 1-ի միջև: (Բանակում ընդունված է 12-ից հետո հաշվել  ժամը 13, 14 և այլն, բայց առօրյայում այդպիսի նշանակում չենք օգտագործում):

Միավորի մասեր

Ինչ սովորական մարդն արեց չափման սովորական միավորների հետ, կարող են նաև մաթեմատիկոսներն անել իրենց վերացական թվերի հետ: Ինչո՞ւ միավորը չբաժանեն երկու, երեք, չորս և այլն  հավասար մասերի: Որպեզի այդպիսի բաժանումն անիմաստ չլինի, պետք է միավորի այդ մասերին անուններ տալ: Հետո պետք է միավորի մասերի համար հարմար նշան գտնել: Եվ, վերջապես, պետք է մշակել համակարգ, որը թույլ կտա այդ մասերի հետ սովորական թվաբանական գործողություններ կատարել:

Հետո, եթե թվերի մասերով կարելի է գործողություններ անել, ինչպես սովորական թվերով, նշանակում է, որ թվերի մասերը ինչպես գործնական, այնպես էլ տեսական հարցերում կարելի է դիտարկել որպես սովորական թվեր:

Թվերի մասերի անունները եկել են առօրյա խոսքից: Երկու հավասար մասերն անվանում են կես: Մասերը, որ ստացվում են թիվը ինչ-որ քանակի մասերի բաժանելուց, անվանում են այդ  մասերի քանակին համապատասխան անուններով՝ այսինքն` երրորդ, չորրորդ, հինգերորդ և այլն: Կեսը ստանում են միավորը երկու հավասար մասերի բաժանելուց: Այլ կերպ՝ դա 1:2-ն է: Այսպիսի բաժանման դեպքում մեկ ամբողջ թիվ չենք ստանա, և անիմաստ է այն փնտրել: Պետք է ուղղակի այդ թվաբանական գործողության համար նշանակում ընտրել: Այդ նշանակումը դարձավ 1/2-ը: Դա կարելի է կարդալ կա´մ «մեկ երկրորդ» կամ «կես»: Եթե մենք 1-ը բաժանում ենք 3-ի, ապա ստանում ենք համապատասխանաբար մեկի երրորդ մասը կամ մեկ երրորդ: Եթե բաժանում ենք 5-ի, ստանում ենք մեկ հինգերորդը և այլն: Մենք  չենք փորձի լուծել այդ վարժությունները,   1/2, 1/3, 1/5-ը ուղղակի նշանակումներ են: Երբ ասում ենք, որ 1:3=1/3, ուղղակի հաստատում ենք, որ «3 մասի բաժանած միավորը հավասար է մեկը բաժանած 3-ի»:

Հուսահատեցնո՞ղ է հնչում: Կարող եք հարցնել, իսկ ի՞նչ է այդ միավորը, որ բաժանում ենք 3-ի: Պատասխանը պարզ է՝ ի´նչ կարևոր է: Եթե  կարող եք  մեծության հետ աշխատել, ինչպես սովորական թվի, դա լիովին բավարար է: Միավորի այդ մասերն անվանում են կոտորակներ («կոտորել» բառից): Ի տարբերություն կոտորակների, այն թվերը, որոնց հետ առաջ գործ ունեինք, կոչվում են ամբողջ: Հիմա տեսնենք, թե ինչ գործողություններ կարելի է անել կոտորակների հետ: Պետք է պարզել, թե կոտորակներն ինչպես գումարենք և հանենք: Ենթադրենք, անհրաժեշտ է գումարել  1/3 և 1/3: Բառերով հեշտ է բացատրելը: Մեկ երրորդը և մեկ երրորդը միասին երկու երրորդ կդառնան (ինչպես եթե մեկ խնձորին մեկ խնձոր ավելացնես, հավասար կլինի երկու խնձորի):

Հետո պետք է որոշել, թե ինչպես թվաբանական նշանների օգնությամբ գրառվի այս գործողությունը: Քանի որ մեկ երրորդը 1/3-ն է, տրամաբանական է ենթադրել, որ երկու երրորդը կլինի 2/3։ Բայց ի՞նչ է նշանակում այդ մեծությունը: Ի՞նչպես 2-ը բաժանենք 3-ի: Պատկերացնենք` երկու կտոր կարկանդակ ունենք, իսկ երեխաները երեքն են: Երբ յուրաքանչյուր կարկանդակը երեք մասի բաժանենք, վեց կտոր կլինի: Արդեն յուրաքանչյուր երեխայի կարելի է երկու կտոր տալ: Այսպիսով յուրաքանչյուր երեխա կստանա 2/3:

Այսպես դատելով` կարող ենք ցույց տալ, որ ցանկացած բաժանման արդյունք կարելի է ներկայացնել կոտորակի տեսքով: Քառասուներեք կարկանդակը բաժանենք յոթանասուներեք մարդու, արդյունքում  կստանանք 43/72, այսինքն` յուրաքանչյուրը կստանա  կարկանդակի 43/72 կտոր:

Վերադառնանք բազմապատկմանն ու բաժանմանը: Ցույց տվեցինք, թե ինչի է հավասար 1/5+1/5+1/5, նույն ձևով կարելի է ցույց տալ նաև, որ 1/5+1/5+1/5=3/5, իսկ 3/5-2/5=1/5:

Ընդհանուր կանոն դուրս բերեցինք: Նույն հայտարարն (հայտարար կոչվում է կոտորակի  այն մասը, որը գտնվում է գծից ցած) ունեցող կոտորակների գումարման և հանման ժամանակ անհրաժեշտ է առաջին կոտորակի համարիչից հանել երկրորդ կոտորակի համարիչը:

Այդ նույն կանոնը գործում է նաև կոտորակի և ամբողջ թվի բազմապատկման ժամանակ: Բազմապատկում են միայն կոտորակի համարիչը: 1/7-ը 6-ով բազմապատկելիս ստանում ենք   6/7, իսկ 18/23-ը 9-ի բաժանելիս կստանանք 2/23: Ճիշտ այդպես էլ խնձորների դեպքում է. մեկ խնձորը բազմապատկելով 6-ով, 6 խնձոր կստանանք, իսկ 18 խնձորը բաժանելով 9-ի, երկու խնձոր կլինի: Գումարման ժամանակ հնարավոր է, որ համարիչը հասնի հայտարարի մեծությանը: Օրինակ՝ 1/3+1/3+1/3=3/3 կամ 3x1/3=3/3: Ինչի՞ է հավասար 3/3-ը:

Ակնհայտ է, եթե միավորը բաժանենք երեք մասի, իսկ հետո նորից այդ երեք մասերը գումարենք, կստանանք սկզբնական թիվը, այսինքն` միավոր: Այլ կերպ ասած` 3/3=1, և այս արտահայտությունը համապատասխանում է կոտորակի մեր սահմանմանը, այսինքն` 3:3=1.

Ճիշտ այդպես էլ 2/2-ը, 4/4-ը, 27/27-ը, 109476/109476-ը հավասար են մեկի:

Իսկ ի՞նչ անենք, եթե պետք է 1/3-ը բազմապատկել 4-ով: Կստանանք 4/3, իսկ ի՞նչ է նշանակում այսպիսի արտահայտությունը:

4/3 կոտորակը կարելի է ներկայացնել 1+1/3,  կամ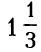 տեսքով, կամ մեկ ամբողջ մեկ երրորդ:

Դպրոցում աշակերտներին, սովորաբար, վարժեցնում են, որպեսզի կոտորակի հնարավորինս մեծ ամբողջ մաս առանձնացնեն: Այսինքն 4/3-ը ներկայացնել 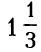 տեսքով, 27/5-ը՝  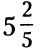տեսքով: Սակայն այդ ձևփոխությունը ոչ միշտ է անհրաժեշտ:

Իրականում 4/3-ով և 27/5-ով թվաբանական գործողություններ կատարելն ավելի հարմար է, քան 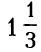 –ով և 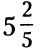 -ով: Ըստ Էության, կոտորակի ամբողջ մասն առանձնացնելու ձգտումն առաջացել է միայն բնական պահպանողականության, այլ ոչ թե նպատակահարմարության նկատառումներից:

Մեկից փոքր կոտորակները, այսինքն այն կոտորակները, որոնց համարիչը փոքր է հայտարարից, անվանում են կանոնավոր կոտորակներ: Եվ հակառակը, կոտորակները, որոնց համարիչը մեծ է հայտարարից, անվանում են անկանոն, այսինքն` այս կոտորակների անվանումն իսկ հավանություն չտալու երանգ ունի:
Այնուամենայնիվ, չի կարելի մոռանալ, որ բոլոր կոտորակների հետ գործողություններն իրականացվում են նույն կանոնով: Մաթեմատիկական տեսանկյունից և´ այս, և´ մյուս կոտորակները հավասար չափով կանոնավոր են:

Խաղի մեջ է մտնում հայտարարը

Դիտարկենք 6/3 կոտորակը: Նրա մեծությունը 2 է, քանի որ 6/3=6:3=2: 

Ի՞նչ կլինի, եթե հայտարարն ու համարիչը բազմապատկենք 2-ով: Ակնհայտ է, որ կոտորակի մեծությունը չփոխվեց, քանի որ 12/6-ն էլ է հավասար 2-ի: Կարելի է նաև հայտարարն ու համարիչը բազմապատկել 3-ով և ստանալ 18/9, կամ 27-ով՝ 54/27, կամ 101-ով` 606/303: Այս դեպքերից յուրաքանչյուրում կոտորակի արժեքը, որը ստացվում է համարիչը հայտարարին բաժանելով, 2 է: Սա նշանակում է, որ կոտորակի մեծությունը չի փոխվել: Այսպիսի օրինաչափություն նկատվում է նաև մյուս կոտորակների դեպքում: Եթե 120/60 կոտորակի համարիչն ու հայտարարը (մեծությունը 2 է) բաժանենք 2-ի (արդյունքը` 60/30), կամ 3-ի (արդյունքը` 40/20), կամ 4-ի (արդյունքը` 30/15) և այլն, յուրաքանչյուր դեպքում կոտորակի մեծությունն անփոփոխ է մնում և հավասար 2-ի: Այս կանոնը տարածվում է նաև այն կոտորակների վրա, որոնց արժեքը ամբողջ թվի հավասար  չէ: Եթե 1/3 կոտորակի համարիչն ու հայտարարը բազմապատկենք 2-ով, արդյունքում 12/6 կստացվի, այսինքն` կոտորակի արժեքը չփոխվեց: Իսկապես, եթե կարկանդակը բաժանեք 3 մասի և վերցնեք մեկը կամ բաժանեք 6 մասի և վերցնեք 2-ը, երկու դեպքում էլ կունենաք նույն մեծության կարկանդակ: Հետևաբար, 1/3 և  2/6 թվերը նույնական են:

Ձևակերպենք ընդհանուր կանոն: Ցանկացած կոտորակի համարիչն ու հայտարարը կարող ենք բազմապատկել կամ բաժանել միևնույն թվով, և այդ դեպքում կոտորակի արժեքը չի փոխվում: Այս կանոնը շատ օգտակար է: Օրինակ, այն թույլ է տալիս մի շարք դեպքերում, բայց ոչ միշտ, խուսափել մեծ թվերի հետ գործողություններից:

Օրինակ կարող ենք 126/189 կոտորակի համարիչն ու հայտարարը բաժանել 63-ի և կստանալ 2/3, որով ավելի հեշտ է հաշվարկ անելը: Եվս մեկ օրինակ: 155/31 կոտորակի համարիչն ու հայտարարը կարող ենք բաժանել 31-ի և կստանանք 5/1 կոտորակը կամ 5, քանի որ 5:1=5: Այս օրինակում առաջին անգամ հանդիպեցինք կոտորակի, որի հայտարարը 1 է: Հաշվարկների ժամանակ այսպիսի կոտորակները կարևոր դեր են խաղում: Անհրաժեշտ է հիշել, որ ցանկացած թիվ կարելի է բաժանել 1-ի, ընդ որում նրա արժեքը չի փոխվի: Այսինքն`273/1-ը հավասար է 273, 509993/1-ը հավասար է 509993 և այլն:

Հետևաբար, կարող ենք թվերը չբաժանել ամբողջների և կոտորակների, քանի որ յուրաքանչյուր ամբողջ թիվ կարելի է ներկայացնել 1 հայտարար ունեցող կոտորակի տեսքով:

Այսպիսի կոտորակների հետ, որոնց հայտարարը 1 է, կարելի է կատարել նույն թվաբանական գործողությունները, ինչ և մնացած կոտորակների հետ՝ 15/1+15/1=30/1, 4/1x3/1=12/1:

Կարող եք հարցնել, թե ինչ օգուտ նրանից, որ ամբողջ թիվը ներկայացնենք 1 հայտարար ունեցող կոտորակի տեսքով, չէ՞ որ ամբողջ թվի հետ աշխատելը հարմար է: Հարցն այն է, որ երբ միևնույն ժամանակ գործ ունենք ամբողջ և կոտորակային թվերի հետ, ամբողջ թվի ներկայացումը կոտորակով` արդյունավետ տարբեր գործողություններ կատարելու հնարավորություն ենք ստանում:

Ենթադրենք, պետք է գումարենք 1/3 և 1/5 թվերը: Գիտենք, որ գումարել կարելի է միայն այն կոտորակները, որոնց հայտարարները հավասար են: Կնշանակի, որ պետք է սովորենք կոտորակները այնպիսի տեսքի բերել, որ հայտարարները հավասար լինեն: Այս դեպքում նորից պետք կգա այն, որ կոտորակի համարիչն ու հայտարարը, առանց նրա արժեքը փոխելու, բազմապատկենք նույն թվով:

Ս կզբում 1/3 կոտորակի համարիչն ու հայտարարը  5-ով բազմապատկենք: Կստանանք 5/15. կոտորակի արժեքը չփոխվեց: Այնուհետև 1/5 կոտորակի համարիչն ու հայտարարը բազմապատկենք 3-ով: Կստանանք՝  3/15, նորից կոտորակի արժեքը չփոխվեց: Հետևաբար, 1/3+1/5= 5/15+3/15=8/15: 

Այժմ փորձենք այս համակարգը կիրառել ինչպես ամբողջ, այնպես էլ կոտորակային թվեր պարունակող գումարման դեպքում:

Պետք է գումարենք 3+1/3+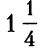: Սկզբում բոլոր գումարելիները բերենք կոտորակի տեսքի. կստանանք 3/1+1/3+5/4: Այժմ բոլոր կոտորակները բերենք նույն հայտարարի, դրա համար պետք է առաջին կոտորակի համարիչն ու հայտարարը բազմապատկենք 12-ով, երկրորդը՝ 4-ով, երրորդը՝ 3-ով: Արդյունքում կստանանք՝  36/12+4/12+15/12, որն էլ հավասար է 55/12: Եթե ուզում եք ազատվել անկանոն կոտորակից, այն կարելի է ներկայացնել ամբողջ և կոտորակային մասեր ունեցող թվի տեսքով`55/12=48/12+7/12 կամ  :

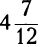Զրոյից փոքր կոտորակներ

Հենց նոր սովորած բոլոր կանոնները, որոնք թույլ են տալիս կոտորակներով գործողություններ կատարել, ճիշտ են նաև  բացասական թվերի դեպքում: Այսպես` -1:3 արտահայտությունը կարելի է գրել նաև -1/3, իսկ 1:(-3)-ը՝ 1/-3 տեսքով: Քանի որ, ինչպես բացասական թիվը դրական թվի բաժանելու, այսպես էլ դրական թիվը բացասականի բաժանելու արդյունքում բացասական թիվ ենք ստանում, երկու դեպքում էլ պատասխանը բացասական թիվ է ստացվում: Այսինքն` (-1):3=-1/3, կամ 1:(-3)=-1/3: Այսպիսի գրության դեպքում մինուս նշանը վերաբերում է ամբողջ կոտորակին, ոչ թե առանձին համարիչին կամ հայտարարին: Մյուս կողմից, (-1):(-3) արտահայտտությունը կարելի է գրառել նաև  -1/-3, և քանի որ, բացասական թիվը բացասական թվի բաժանելու դեպքում դրական թիվ ենք ստանում, ապա -ը կարելի է գրել այսպես +1/3: Բացասական կոտորակների գումարումն ու հանումը կատարում են նույն կերպ, ինչպես դրական կոտորակների գումարումն ու հանումը: Օրինակ՝ ինչ է նշանակում 1-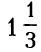: Երկու թիվն էլ կոտորակի տեսքով ներկայացնենք 1/1-4/3: Կոտորակները բերենք ընդհանուր հայտարարի և կստանանք՝ 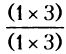-4/3, այսինքն 3/3-4/3 կամ -1/3:

Շարունակությունը

Թարգմանություն ռուսերենից 
Լուսանկարը` Լիանա Հակոբյանի բլոգից