Գաղափարի ծնունդը

Մաթեմատիկական հայտնություն

9-րդ գլուխը

Գլուխ 10

Բայց իմ մտքում փայլատակեց մի նոր լույս 
Եվ ինձ պարզեց խորհուրդը այդ տեսիլքի։
Դանթե, Դրախտ, Երգ XXXIII

§1. Լույսի առկայծում

Խնդրի լուծումը կարող է միանգամայն անսպասելիորեն հայտնվել: Երկար ժամանակ խնդիրը փորփրում էինք առանց նկատելի ինչ-որ առաջընթացի, և հանկարծ մեր գլխում գերազանց գաղափար է փայլատակում, ոգեշնչման բռնկում, հանկարծ մթության մեջ տեսնում ենք լույսի առկայծումը։ Դա նման է այն  բանին, երբ ուշ գիշերով մտնում ես հյուրանոցային անծանոթ համար, որտեղ նույնիսկ չգիտես, թե լույսը որտեղից են միացնում: Մթության մեջ փնտրում ես անջատիչը, դեմ ես առնում ինչ-որ կահույքի, շոշափում ես ինչ-որ սուր անկյուններ, անձև զանգվածներ: Բայց ահա անջատիչը գտնվեց, լույսը միացրիր, և ամեն ինչ իր տեղն ընկավ: Անձև զանգվածները որոշակիացան, ծանոթ առարկաների ուրվագծեր ընդունեցին, ընդ որում պարզվեց, որ այդ առարկաները տեղադրված են այնտեղ, որտեղ և պետք է լինեին, և որ շատ լավ են հարմարեցված՝ իրենց նշանակությամբ կիրառվելու համար:

Հենց այսպես կարող են երևալ խնդիր լուծողի ապրումները, որ նրան ուղեկցում են խնդիրը լուծելիս. գաղափարը հանկարծակի առկայծում է, որը մինչ այդ անորոշ, ցրված, խճճված թվացող մասերի միջև բերում է պարզություն, կարգ, կապ ու նպատակահարմարություն:

Սակայն նման հարցերում սեփական փորձի հատիկն ավելի թանկ է, քան մի տոննա նկարագրությունը: Ծանոթանալու համար, թե ինչ է այդպիսի անձնական փորձը, մեզ ինչ-որ կոնկրետ օրինակ է պետք: Հնարավոր է, որ այդ նպատակին ամենահարմարը մաթեմատիկական պարզ օրինակներն են. նրանք կարող են մեզ աշխատանքի նյութ տալ, անհանգստություն և հայտնագործության հրճվանք զգալու հնարավորություն և «վարժեցնեն մեր աչքերը՝ ճշմատությունը տեսնելու պարզ և հստակ» (վերջին արտահատությունը Դեկարտից եմ փոխ առել):

§ 2. Օրինակ

Ինձ ազատություն կտամ և կփորձեմ մի փոքր փորձ կատարել ընթերցողի հետ: Կձևակերպեմ հասարակ, բայց ոչ շատ ծեծված երկրաչափական խնդիր, իսկ հետո կփորձեմ վերականգնել դրա ապացույցին տանող գաղափարների հաջորդականությունը: Մտադիր եմ դանդող առաջ գնալ, շատ դանդաղ, հաջորդաբար բացելով գաղտնիքները, ընդ որում՝ այդ գաղտնիքներից յուրաքանչյուրը բացելով ոչ թե միանգամից, այլ՝ աստիճանաբար: Հուսով եմ, որ նախքան պատմության վերջին հասնելը, ընթերցողը կկարողանա որսալ գլխավոր գաղափարը (եթե, իհարկե, ինչ-որ բան դրան չխանգարի), և քանի որ այդ գաղափարը շատ անսպասելի կլինի, նա կկարողանա բավարարվածություն ապրել իր ոչ մեծ բացահայտումից:

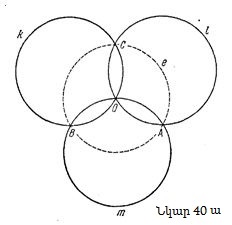Ա. Եթե նույն շառավիղն ունեցող երեք շրջանագծեր անցնում են մի կետով, նույն շառավիղը կունենա նաև այն շրջանագիծը, որ անցնում է դրանց հատումների մյուս երեք կետերով:

Սա էլ հենց այն թեորեմն է, որը պետք է ապացուցել: Թեորեմի պնդումը կարճ է և պարզ, բայց այնտեղ կարծես ինչ-որ բան է պակասում: Գծագրելով (նկ. 40ա) և հարմար նշանակումներ ներմուծելով՝ հանգում ենք խնդրի ավելի մանրամասն տարբերակին:

Նույն r շառավղով երեք՝ k, l, m շրջանագծերը անցնում են նույն O կետով:  l և m շրջանագծերը հատվում են A կետում, m և k շրջանագծերը՝ B կետում, k և l շրջանագծերը՝ C կետում: Պահանջվում է ապացուցել, որ A, B և C կետերով անցնող e շրջանագիծը կունենա նույն r շառավիղը:

40ա նկարում պատկերված են k, l, m և e շրջանագծերը և նրանց հատման չորս կետերը: Սակայն այս գծագիրը կարող է բավարար չթվալ, քանի որ այնքան էլ պարզ չէ և ամբողջական չէ. տպավորություն է ստեղծվում, որ այնտեղ ինչ-որ բան պակասում է. թվում է, որ ինչ-որ էական բան հաշվի չի առնված:

Հիմա գործ ունենք շրջանագծերի հետ: Ի՞նչ է շրջանագիծը: Յուրաքանչյուր շրջանագիծ որոշվում է իր կենտրոնի դիրքով և շառավղով՝ շրջանագծի բոլոր կետերը նրա կենտրոնից նույն հեռավորության վրա են: Բայց մոռացել ենք դիտարկել այդ չորս շրջանագծերի համար ընդհանուր r շառավիղը. այսպիսով, ուշադրություն չենք դարձրել պայմանի էական մասին: Եկեք սկզբում նշանակենք մեր շրջանագծերի կենտրոնները՝ k շրջանագծինը՝ K, l շրջանագծինը՝ L, m շրջանագծինը՝ M տառերով: Որտե՞ղ է ամենահարմարը գծել r շառավիղը: Հավանաբար, իմաստ չունի առավելություն տալ k, l, m շրջանագծերից որևէ մեկին կամ հատման A, B, C կետերից որևէ մեկին: Այդ պատճառով էլ, թերևս, միացնենք երեք կենտրոններից յուրաքանչյուրը այդ շրջանագծերին պատկանող հատման կետերին՝ K-ն B, C, O կետերին և այլն:

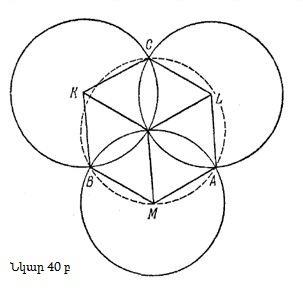
Ստացված գծագիրը (նկար 40բ) հուսահատեցնող ծանրաբեռնված է:

Այնտեղ ուղիղ և կոր այնքան գծեր կան, որ հնարավոր չէ «մի հայացքով ընդգրկել». «տեղում չի մնում»: Այս պատկերը կարող է հիշեցնել հին ամսագրերից ծանոթ որոշ նկարներ, այդպիսի նկարը դիտավորյալ մի քիչ անորոշ են անում. եթե դրան ուղիղ նայես, մի պատկեր կտեսնես, իսկ եթե ամսագիրը թեքես՝ որոշակի հատուկ դիրք տալով, և նկարը դիտես որոշակի անկյան տակ, հանկարծ ուրիշ պատկեր է երևում, որը զարմացնում է որպես առաջինի շատ թե քիչ սրամիտ մեկնաբանություն: Կարո՞ղ եք մեր խճճված՝ ուղիղներով և շրջանագծերով ծանրաբեռնված գծագրի վրա գտնել մեկ ուրիշ, հնարավոր է, մեր նպատակների համար ավելի օգտակար պատկեր:

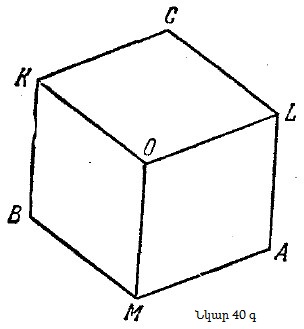
Մեզ պետքական այդ պատկերը, որը թաքնված է մեր ծանրաբեռնված գծագրի խճճված գծերի մեջ, կարող ենք նկատել կա՛մ պատահաբար, կա՛մ աստիճանաբար: Փնտրվող գծագրին մեզ կարող են հասցնել այն ճիգերը, որոնք գործադրում ենք տրված խնդիրը լուծելիս, կամ ինչ-որ երկրորդական, ոչ էական հանգամանք: Այսպես, օրինակ, երբ զբաղված էինք մեր անկատար գծագիրը գծելով, կարող էինք նկատել, որ ամբողջ պատկերը լրիվ որոշվում է նրա կազմում մտնող «ուղղագիծ» (հատվածներից բաղկացած) մասով (նկար 40գ):   

Վերջին հանգամանքը մեզ կարևոր է թվում: Այն էականորեն պարզեցնում է նկարի երկրաչափությունը և, հնարավոր է, որ պարզաբանում է գործի տրամաբանությունը: Եվ այն բերում է մեր թեորեմի հետևյալ փոփոխված ձևակերպմանը.

Բ. Եթե հետևյալ ինը հատվածներից յուրաքանչյուրը՝

               KO,               KB,               KC
               LC,                LO,               LA
               MB,               MA,              MO

հավասար է r, գոյություն ունի այնպիսի E կետ, որ հետևյալ հատվածներից յուրաքանչյուրը՝

               EA,                EB,                EC

նույնպես r կլինի:

Վերջին պնդումը մեր ուշադրությունն ուղղում է 40գ նկարին: Այս նկարը ինչ-որ բանով ուշագրավ է. այն ինչ-որ ծանոթ բան է հիշեցնում: (Հատկապես ի՞նչ):

Իհարկե, 40գ նկարում պատկերված քառանկյուններից յուրաքանչյուրի, օրինակ՝ OLAM-ի, բոլոր չորս կողմերը հավասար են միմյանց, այսինքն՝ դրանք բոլորը շեղանկյուն են: Շեղանկյունը մեզ քաջ ծանոթ պատկեր է. այն մտովի առանձնացնելով մեր գծագրում՝ պատկերը կարող ենք ավելի լավ «տեսնել»:

Շեղանկյան հակադիր կողմերը զուգահեռ են: Հենվելով այդ հանգամանքին, կարելի է 40գ գծագրի պատկերը կազմող 9 հատվածները բաժանել երեք խմբի, որոնցից յուրաքանչյուրում միմյանց զուգահեռ հատվածներ են, օրինակ՝ հատվածների այդպիսի մի խմբում են AL, MO, BK հատվածները: (Հիմա ի՞նչ կարող է հիշեցնել մեզ այդ պատկերը):

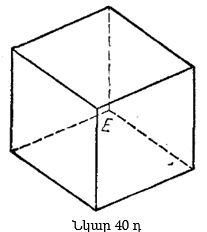
Պետք է չմոռանանք այն նպատակը, որին ձգտում ենք: Ենթադրենք, որ թեորեմի եզրակացությունը ճիշտ է: Գծագրի վրա նշելով e շրջանագծի E կենտրոնը և A, B, C կետերում վերջացող երեք շառավիղները (նկար 40դ)՝ ստանում ենք (ենթադրաբար) նոր շեղանկյուններ, նոր զուգահեռ հատվածներ: (Հիմա ամբողջ պատկերն ի՞նչ է հիշեցնում):

Իհարկե, 40դ նկարը ներկայացնում է զուգահեռանիստի 12 կողերի պրոյեկցիան՝ տեղադրված այնպես, որ բոլոր պրոյեկցիաները ունեն նույն երկարությունը:

Նկար 40գ-ն «անթափանց զուգահեռանիստի» պրոյեկցիան է. տեսնում ենք միայն 3 նիստերը, 7 գագաթները և 9 կողերը, մինչդեռ 3 նիստերը, 1 գագաթը և 3 կողերը գծագրի վրա չեն երևում: Այս պատկերը 40դ նկարի մասն է, բայց այնպիսի մասը, որը որոշում է մեզ հետաքրքրող ամբողջ պատկերը: Եթե զուգահեռանիստը և պրոյեկտման ուղղությունը այնպես են ընտրված, որ 40գ նկարի վրա պատկերված ինը կողերի պրոյեկցիաները հավասար են r (այսինքն, այնպիսին են, որ պետք է լինեին խնդրի պայմանի համաձայն), մնացած երեք կողերի պրոյեկցիաներն էլ պետք է հավասար լինեն r: Ութերորդ՝ չերևացող E գագաթի պրոյեկցիայից դուրս են գալիս r երկարությամբ երեք հատված, իսկ այդ պրոյեկցիան A, B, C կետերով անցնող և r շառավղով շրջանագծի կենտրոնն է:

Մեր թեորեմը ապացուցված է, ընդ որում ապացուցված է անսպասելիորեն սրամիտ գաղափարով, այն է, որ մենք հարթ պատկերը դիտարկում ենք որպես տարածական մարմնի պրոյեկցիա:

Այս ապացույցում տարածաչափական հասկացություններ են օգտագործվում: Ինձ թվում է՝ մեծ փորձանք չէ, մանավանդ որ հեշտ ուղղվող է: Իսկապես, քանի որ գիտենք, որ E կենտրոնի դիրքը կարող է շատ հեշտությամբ բնութագրվել, EA, EB, EC հատածների երկարությունները կարելի է ընդգրկել՝ առանց տարածաչափությանը դիմելու: Սակայն այստեղ չենք պնդիր այդ տեսակետը:

§ 3. Օգտակար գաղափարի բնութագրիչ կողմերը        

Հենց նոր հարմար օրինակի վրա ցուցադրեցինք օգտակար գաղափարը բնութագրող տարբեր գծեր: Նրա ծնունդը ցուցադրեցինք շատ դանդաղ: Ամբողջ ձայնով հաղթական իր մասին հայտնելու փոխարեն մեզ ներկայացավ որպես խեղճ կակազող[1]: Ճիշտ է, դա մտածված էր արված, որպեսզի ընթերցողին հնարավորություն տրվեր մասնակցելու մաթեմատիկական փաստը բացահայտելուն: Մեր օրինակը կարող է մի քիչ միակողմանի թվալ նաև այլ իմաստով, ինչը, սակայն, անխուսափելի է, քանի որ գաղափարները իրենք շատ բազմազան են: Սակայն, եթե ընթերցողը մեր օրինակը դիտարկի բարյացակամ ըմբռնումով, հարկ եղած լույսի ներքո, համապատասխան շրջանակում, սեփական փորձի ֆոնին, նրա համար օրինակն օգտակար ցուցադրություն կլինի տարբեր հատկանիշների, որոնք բնորոշ են օգտակար գաղափարներին և բավականին հաճախ են հանդիպում: 

Շատ հաճախ օգտակար գաղափարը հանկարծակի է առաջանում: Այն շատ էական նոր տարր է ներմուծում և փոխում է մեր տեսակետը: Նրանից հետո գալիս է հաստատուն վստահություն, որ նպատակը հասանելի է:

Հանկարծակիությունը շատ բնորոշ հատկանիշ է, բայց այն նկարագրելը շատ դժվար է: Եթե 40բ նկարը ուսումնասիրելուց հետո ընթերցողի աչքին զուգահեռանիստի պատկերը հանկարծ «բարձրացավ» գծերի և տառերի խառնաշփոթից, նա լավ կհասկանա, թե խոսքն ինչի մասին է: Հավանական է, որ նրան ինչ-որ չափով պարզ կլինի, թե ինչ պետք է հասկանալ ոգեշնչում ասելով, և ինչու տպավորիչ գաղափարի հանկարածակի հայտնվելը երբեմն նկարագրում են որպես հազիվ լսելի հուշում, որի համար պարտական ենք մեր ներքին զգացողությանը, կամ որպես նշան, որը տրվել է գերբնական էակի կողմից:

Նշենք, որ մեր թեորեմը ապացուցելիս առաջացած ամենակարևոր տարրը զուգահեռանիստի մասին գաղափարն էր: Բավականին զարմանալի է, որ տարածական մարմինը դարձավ հարթաչափական խնդրի լուծման բանալին: Շատ ավելի են այն դեպքերը, երբ կարևոր տարրը թաքնված է այն բնագավառում, որին ինքը խնդիրն է պատկանում: Եթե հարթաչափական խնդիր է, կարելի է սպասել, որ կարևոր տարրը կլինի գծագրում ավելացրած նոր գիծ, կամ անսպասելիորեն մտաբերած թեորեմ, կամ դրա նման ինչ-որ բան:

Մեր դեպքում իրերին սովորական հայացքի փոփոխությունը շատ ազդու երևաց: Շրջանագծերը նահանջեցին ետին պլան և հետո լրիվ անհետացան. առաջին պլան եկան ուղիղ հատավծներ, ընդ որում դադարեցինք դրանք որպես շառավիղներ ընկալել և կապեցինք ինչ-որ զուգահեռանիստի հետ: (Որտեղի՞ց հայտնվեց): Նախկին շառավիղները, դրանց ծայրակետերը, այդ շառավիղներով կազմաված քառանկյունները, նոր իմաստ ձեռք բերեցին՝ նրանք համապատասխանաբար դարձան տարածական մարմնի կողեր, գագաթներ և նիստեր: Խնդրին պատկանող տարրերին վերաբերող տեսակետը ոչ միայն ցուցադրական է, այլև տիպական: Խնդիրը լուծող ցանկացած գաղափար բերում է իրերի նկատմամբ ընդհանուր հայացքի այդպիսի հեղափոխական վերակառուցման, և սա վերաբերում գրեթե յուրաքանչյուր խնդրի լուծմանը: Գաղափարի առաջանալու հետ միաժամանակ խնդրի տարրերը սկսում են նոր դեր խաղալ, նոր իմաստ են ձեռք բերում: Երկրաչափական խնդրի լուծման պրոցեսում նրա տարրերը փոխվում են տեղերով և վերախմբավորվում են՝ նրանք կազմում են եռանկյուններ կամ համապատասխան կողմերով եռանկյունների զույգեր, կամ շեղանկյուններ, կամ ծանոթ ուրիշ փոխդասավորություններ, որոնք ծառայում են ուսումնասիրության նպատակներին: Գիծը, որը մինչև օգտակար գաղափարի ծնվելը ուղղակի գիծ էր, նոր իմաստ է ձեռք բերում՝ դառնում է եռանկյան կողմ, որի հավասարությունը մեկ այլ եռանկյան շատ էական է դառնում խնդրի լուծման համար, կամ այդ գիծը դառնում է երկու զուգահեռ ուղիղների հատող, կամ ինչ-որ ուրիշ կերպ մասնակցում է վերջնական գծագրում: Գաղափարի հայտնվելուց հետո մենք ավելի շատ ենք տեսնում՝ ավելի շատ իմաստ, ավելի շատ հեռանկար և ավելի շատ հարաբերակցություն: Գաղափարի հայտնվելը նման է մութ սենյակում լուսավորությունը միացնելուն:

Օգտակար գաղափարն առաջանում է վստահության հետ միաժամանակ, որ նպատակը հասանելի է: Հանկարծակի ծագած գաղափարը ցուցադրում է նոր ազդեցիկ քայլ դրամատիկ անկարգության մեջ, տպավորություն է ստեղծում իր կարևորությամբ, իր հետ բերում է հաստատ վստահություն: Այդ վստահությունը սովորաբար արտահայտվում է այսպիսի բացականչություններով. «Դե, արդեն վերջ», «Վերջապես գտա այն, ինչը պետք էր», «Այ թե ինչն էր խորամանկությունը», «Հասկանալի է»: Մեր օրինակում զուգահեռանիստը նկատելը դեռ բավարար չէր, եթե չեք նկատել, որ հենց դա է բերելու խնդրի լուծմանը, ուրեմն դեռ չունեք խնդիրը լուծող գաղափարը: Ձեզ ավելին է պետք: Իհարկե, պետք չէ բոլոր մանրամասներով տեսնել, թե զուգահեռանիստը ինչպես է հասցնում խնդիրը լուծելուն, բայց պետք է անկասկածելի զգացողություն առաջանա, որ անպայման կտանի դրան:  

§ 4. Գաղափարի կախվածությունը պատահականությունից

Պատահաբար հանգել եք գաղափարի՞: Եթե պատասխանեք «այո», ուրեմն ձեր բախտը բերել է: Չէ՞ որ դուք չեք կարող ստիպել գաղափարին հայտնվել այն ժամանակ, երբ ցանկանում եք: Ես իմ առաջ որոշակի խնդիր եմ դրել: Ես նրանով լրջորեն եմ զբաղվում. այն հստակ ձևակերպել եմ ինձ համար, պարզորոշ պատկերացնում եմ այն: Ես խորացել եմ իմ խնդրում և … Սպասում եմ օգտակար գաղափարի, բայց այն կհայտնվի՞: Հնարավոր է, որ կհայտնվի, ընդ որում անմիջապես. հնարավոր է՝ կհայտնվի որոշ ժամանակ հետո, իսկ հնարավոր է, որ ցանկալի գաղափարը ընդհանրապես չհայտնվի:

Կարիք ունենք արգասաբեր գաղափարների. բնական է, որ ձգտում ենք արգասաբեր գաղափարներ ունենալ ձեռքի տակ, մեր տրամադրության տակ: Բայց իրականում գաղափարներն են մեզ տնօրինում, նրանք մեր տերերն են և ինքնակամ են: Իհարկե, նրանք կարող են մեզ հանկարծակի համակել, բայց ավելի հաճախ նրանք ուշանում են, երբեմն նրանք ստիպում են իրենց շատ երկար սպասել, իսկ երբեմն ընդհանրապես հրաժարվում են մեզ ծառայելուց: Գաղափարները գալիս են, երբ իրենք են ցանկանում, այլ ոչ այն ժամանակ, երբ մենք ենք սպասում: Գաղափարին սպասելը նույնն է, ինչ սպասել վիճակախաղով շահելուն:

Իսկ եթե համաձայնենք, որ գաղափարները պատահական հյուր են, խնդրի լուծումը պետք է հիմնականում կախված լինի երջանիկ պատահականությունից: Շատերը կարծում են, որ հենց այդպես է: Սեմյուել Բաթլերն[2] այդ միտքն արտահատել է սրամիտ քառյակով [3].

Աշխարհի բոլոր գյուտերի պատճառը
Ոչ առաջինը դրանց արարելն է, ոչ էլ արդյունքը ուղեղի աշխատանքի
Առանձին մարդկանց բախտը բերել է՝
Հանգեն դրանց սխալմամբ կամ էլ վրիպումով[4]։

Դժվար է հավատալը, որ այդքան լայնորեն տարածված կարծիքը կարող է ամբողջովին հիմքից զուրկ լինել, որ այն լրիվ սխալ է: Իսկ ամբողջությա՞մբ է այն ճշմարիտ: Եվ արդյո՞ք ամեն անգամ խնդիր լուծելիս պետք է հույսներս ամբողջությամբ պատահականությանը թողնենք: Հույս ունեմ, որ նախորդ բոլոր գլուխները կարդալուց հետո ընթերցողն ամեն դեպքում կարողացավ այս մասին որոշակի կարծիք կազմել:

10-րդ գլխին վերաբերող վարժություններ և լրացուցիչ դիտողություններ

1. Գաղափարի հայտնվելու հանկարծակիությունը: Մի մեջբերում և դրա մեկնաբանություն:

1°. Մեջբերենք Թոմաս Փենի[5] գրքից մի հատված։

Յուրաքանչյուր հետազոտող, որ հետազոտում է մարդկային մտքի գործունեությունը և զարգացումը՝ հիմնվելով սեփական մտքի դիտարկումների վրա, չի կարող նկատած չլինել, որ գոյություն ունի երկու տարբեր տեսակ այն բանի, որը միտք է կոչվում. առաջինին պատկանում են նրանք, որ մենք ենք ակտիվորեն առաջացնում մտածողության ակտի միջոցով, խորհրդածելով, երկրորդին՝ նրանք, որոնք մեր գիտակցության մեջ բռնկվում են ինքնակամ: Ես որպես կանոն այդ ինքնակամ եկվորների հետ վարվում եմ մեծագույն քաղաքավարությամբ և ձգտում եմ ուսումնասիրել, որքան թույլ են տալիս կարողություններս, թե նրանք արժանի՞ են ուշադիր ընդունելության. հենց նրանց միջոցով եմ ձեռք բերել բոլոր գիտելիքներս:

2°. Լիխտենբերգը մի անգամ նկատել է, որ պետք չէ ասել «մտածում եմ», այլ՝ «մտածվում է», ինչպես ասում են. «լուսանում է», «ցրտում է». Լիխտենբերգը[6]  պնդում է, որ կան մտածողության ինքնակամ ակտեր, որոնք չենք կարող ղեկավարել, ինչպես չենք կարող ղեկավարել բնության մեծ ուժերը:

Այստեղ կարող ենք ավելացնել, որ մեր բանականությունը երբեմն իրեն պահում է համառ ձիու կամ ջորու նման՝ տարօրինակ կենդանու, որոնց պետք է ընտելանանք և ժամանակ առ ժամանակ առաջ քշենք, որպեսզի նրան ստիպենք մեզ ծառայել, քանի որ, ընդհանրապես ասած, նա հաճախ է մերժում իր ծառայությունները:      

2. Երկու փորձ: Որոշ (բայց ոչ շատ) ժամանակը, որը ծախսում ենք խաչբառեր լուծելու համար, կարող է լավ փոխհատուցվել. այստեղ հնարավորություն է առաջանում ուսումնասիրելու խնդիր լուծելու պրոցեսին վերաբերող ինչ-որ բան, ծանոթանալու, թե ինչպես ենք մտածում, և ինչպես պետք է մտածենք:

1°. Մի խաչբառում կարդացել եք փնտրվող բառի բացատրությունը. «Զգացմունքի բավականին սովորական տեսակ (15 տառ). Սկզբում կարող է ենթադրություն չունենաք, թե ինչ բառ է, կարող է չհասկանաք բացատրությունը: Սակայն տրվածի հետ հատվող բառը, որը կարողացել ենք գտնել, լրացուցիչ ինֆորմացիա է տալիս՝ ցույց է տալիս փնտրվող բառի մեջտեղում մի տառ: Երկրորդ բառը տալիս է երկրորդ տառը, հետո գտնում եք երրորդ տառը, կամ չորրորդը, և հանկարծ փնտրվող բառը «գալիս է ձեր գլուխը»:

Վերցրեք թղթի թերթ և ձեռնամուխ եղեք 422-րդ էջում տեղադրված խնդրի լուծմանը: Սկզբում խնդրի լուծումն ամբողջությամբ ծածկեք թղթով: Նշենք՝ թուղթը ներքև իջեցնելով բացեք միայն առաջին տողը. գլխի ընկա՞ք, թե ինչ բառ է: Եթե ոչ՝ բացեք հաջորդ տողը, հետո՝ նորը և այլն, այսպես գործնականում կծանոթանաք, թե ինչպես է «գաղափարը խփում գլխիդ»:

2°. Եթե գոնե մի քիչ ծանոթ եք մաթեմատիկական անալիզին (շատ քիչ), կարող եք նմանօրինակ աշխատանք անել անորոշ ինտեգրալ հաշվելիս: Վերցրեք թղթի թերթ և բացեք գրքի 422-րդ էջը:

11-րդ գլուխը

Թարգմանություն ռուսերենից 
Լուսանկարը՝ Արևիկ Ներսիսյանի