Խնդիրներ խնդրի մեջ

Մաթեմատիկական հայտնություն

8-րդ գլուխը

Գլուխ 9

Եթե կառուցման կամ ապացուցման ընթացքում ընդունում ենք ինչ-որ բան, որն ավելի վաղ ապացուցված չի եղել, բայց փաստարկում է պահանջում, այդ ենթադրությունը համարում ենք կասկածելի, ուսումնասիրման արժանի և այն անվանում ենք լեմա:
Պրոկլ, Մեկնություններ. Էվկլիդեսի I գրքի 1 նախադասությունը

.... Մի բան իմանալու կախվածությունը մեկ այլ բան իմանալուց,... իսկույն կարող ենք իմանալ՝ ավելի օգտակար չի լինի արդյոք սկզբում ինչ-որ ուրիշ բան ուսումնասիրել, հատկապես՝ ինչը և ինչ կարգով ուսումնասիրել....
Դեկարտ, Մտածողության կանոնների ուղեցույց, Կանոն VI, Ընտիր երկեր, էջ 96

Ձեզ համար ինչպե՞ս է ավելի լավ վարվելը այս խնդրի հետ:Այն հանգիստ թողեք և մի ուրիշ խնդիր մտածեք:
Մաթեմատիկայի ավանդական պրոֆեսոր

§ 1. Օժանդակ խնդիրներ

Մեզ համար մեծ հետաքրքրություն է ներկայացնում Վոլֆգանգ Քյոլերի՝ մարդանման կապիկների դիտարկումները: Ահա այդ փորձերից մեկի սխեմատիկ նկարագրությունը:

Վանդակում շիմպանզե կա, և նա սոված է: Վանդակի դրսի կողմում բանան կա գետնին: Շիմպանզեն կարող է ձեռքը ճաղերի միջով անցկացնել, բայց բանանին չի կարող հասնել: Կապիկը ջանասիրաբար, բայց ապարդյուն փորձել է հասնել բանանին, և ահա նստած է նրա առջև: Վանդակից դուրս, բայց հասանելիության սահմանում, գետնին փայտ կա ընկած, սակայն կապիկը, ըստ երևույթին ոչ մի ուշադրություն չի դարձրել: Հանկարծ շիմպանզեն ակտիվանում է, վերցնում փայտը, անշնորհք կերպով քաշում է բանանը, մինչև կարողանա ձեռքով հասնել, հետո վերցնում է բանանը և ուտում:

Մեր կապիկը երկու խնդիր լուծեց:

Ա. Վերցրեց բանանը:
Բ. Վերցրեց փայտը:

Ա խնդիրը ավելի շուտ էր ծագել, քան Բ խնդիրը: Սկզբում կապիկը փայտի նկատմամբ, որը ուտելու չէր, ոչ մի հետաքրքրություն չէր ցուցաբերում, սակայն նախ լուծեց Բ խնդիրը: Բ խնդրի լուծումը ճանապարհ բացեց սկզբնական Ա խնդիրը լուծելու համար: Կապիկն անմիջական հետաքրքված էր Ա խնդիրը լուծելու և միայն անուղղակի կերպով՝ Բ խնդիրը լուծելու հարցով. Ա-ն վերջնական նպատակն էր, Բ-ն՝ միայն դրան հասնելու միջոց. Ա-ն նրա գլխավոր, հիմնական խնդիրն էր, Բ-ն՝ միայն օգնող («օժանդակ», երկրորդական) խնդիր:

Փորձենք ընդհանուր գծերով նկարագրել այդ կարևոր տերմինի նշանակությունը: Օժանդակ խնդիրն այն խնդիրն է, որին ստիպված ենք ուշադրություն դարձնել, կամ որի վրա պետք է աշխատենք ոչ թե հենց իր համար, այլ այն պատճառով, որ այդ ուշադրությունը կամ աշխատանքը մեզ կօգնեն լուծելու այլ, մեր հիմնական խնդիրը: Օժանդակ խնդիրը նպատակին հասնելու միջոց է, այն մեզ նպատակին հասնելու հնարավորություն է տալիս. սկզբնական խնդիրը նպատակն է և ճանապարհի վերջը:

Անհասանելի թվացող խնդրի լուծման ճանապարհը գտնելը՝ դրա համար հատուկ մտածված, հետո լուծված օժանդակ խնդրի միջոցով, մտավոր գործունեության առավել բնորոշ ցուցադրումներից մեկն է: Եվ շիմպանզեի գործողությունը որպես խելամիտ գործողություն մեկնաբանելուց դժվարությամբ կարող ենք հրաժարվել: Պատրաստվում են օժանդակ խնդիրների դասակարգում անել՝ դրա համար նախօրոք քննելով մի քանի մաթեմատիկական օրինակ:     

§ 2. Համարժեք խնդիրներ. երկկողմանի ռեդուկցիա

Սկսենք հետևյալ օրինակից: Դիցուք, մեր խնդիրն է երեք անհայտով երեք հավասարումների համակարգի լուծումը՝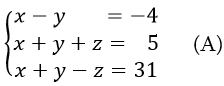

(A) համակարգից անցնենք մեկ ուրիշ՝ (B) համակարգի, որտեղ.

1°. առաջին հավասարումը համընկնում է (A) համակարգի առաջին հավասարման հետ,
2°. երկրորդ հավասարումը (A) համակարգի երկրորդ և երրորդ հավասարումների գումարն է,
3°. երրորդ հավասարումը (А) համակարգի երկրորդ և երրորդ հավասարումներ տարբերությունն է:

Երեք հավասարումների նոր համակարգը հետևյալ տեսքը կունենա.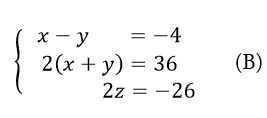

(B) համակարգի ստանալու ձևը ցույց է տալիս, որ (A) համակարգին բավարարող x, y, z թվերը անպայման կբավարարեն և (B)  համակարգին: Ճիշտ է նաև հակառակը՝ (B)  համակարգին բավարարող (x, y, z) թվերը պետք է բավարարեն նաև (A) համակարգին: Սա բավականին ճշմարտանման է թվում, բացի դրանից, կարող է տարբեր ձևերով ապացուցվել. օրինակ այսպես՝ (B)  համակարգի վերջին երկու հավասարումները 2-ի բաժանելով ստանում ենք հետևյալ համակարգը՝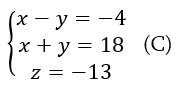

Իսկ (C)-ից կարելի է վերադառնալ (A)-ին՝ (C) համակարգի առաջին հավասարումը թողնելով նույնը, հետո՝ սկզբում գումարելով, իսկ այնուհետև հանելով վերջին երկու հավասարումները: Կարճ ասած՝ եթե x, y, z երեք թվեր բավարարում են (A) և (B) համակարգերից մեկին, նրանք կբավարարեն նաև մյուսին:

(A) և (B) համակարգերը նույնական չեն. նրանք նույն հավասարումները չունեն: Այդ պատճառով էլ, խիստ ասած, չենք կարող պնդել, որ երկու խնդիրները, որոնցից մեկը (A) համակարգը լուծելն է, իսկ մյուսինը՝ (B) համակարգը, նույնական են: Սակայն կարող ենք ասել, որ այդ խնդիրները համարժեք են: Բերենք նշված տերմինի ընդհանուր սահմանումը, որը օգտագործում են մեզ պետքական իմաստով՝ երկու խնդիր համարժեք են, եթե նրանցից մեկի լուծումը հետևում է մյուսի լուծումից:

Մի խնդրից իրեն համարժեք մեկ այլ խնդրի անցնելը կոչվում է երկկողմանի (կամ հակադարձելի, կամ դարձելի, կամ համարժեք) ռեդուկցիա: Այսպես, օրինակ, երկկողմանի ռեդուկցիա էր մեր սկզբնական խնդրից, որն էր (A) համակարգը լուծելը, անցնելը (B) համակարգը լուծելուն: Մեր դեպքում այդպիսի ռեդուկցիան օգտակար էր. (B) համակարգը ավելի հեշտ է լուծելը, քան (A)-ն: Իսկապես, (B)-ն ավելի մոտ է (C)-ին, քան (A)-ն, իսկ (C)-ն գրեթե խնդրի վերջն է. (С)-ն ուղղակի տալիս է z-ի մեզ հետաքրքրող արժեքը, և x-ն ու y-ը գտնելու համար շատ ջանք թափելու հարկ չի մնում:

§ 3. Համարժեք խնդիրների շղթաներ

Վերադառնանք § 2-ի (С) համակարգին. Առաջին և երկրորդ հավասարումները գումարելով և հանելով ստանում ենք նոր համակարգ՝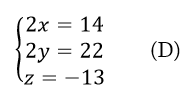

որտեղից էլ՝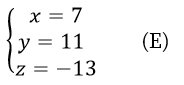

Ունենք հինգ համակարգից բաղկացած հաջորդականություն (որոնցից յուրաքանչյուրը երեք հավասարում ունի)՝ (A), (B), (C), (D), (E)։

Այս համակարգերից յուրաքանչյուրին համապատասխանում է x, y, z անհայտների համար այդ համակարգին բավարարող արժեքները գտնելու խնդիրը: [(E) համակարգի նկատմամբ, որը «խնդրի» լուծման վերջնական գրառումն է, «խնդիր» տերմինը օգտագործվում է ոչ թե բուն, սովորական իմաստով, այլ ընդհանրական իմաստով]: Այս խնդիրներից յուրաքանչյուրը համարժեք է նախորդին (ինչպես նաև հաջորդին), ինչպես շղթայի յուրաքանչյուր օղակը կապված է հարևանների հետ. այստեղ ունենք համարժեք խնդիրների շղթա:

Մեր շղթայում (A)-ն սկիզբն է, իսկ (E)-ն՝ վերջը. (A)-ն հավասարումների ելման համակարգն է, իսկ (Е)-ն՝ արդեն լուծումն է: Սա լուծմանը հասցնող բացարձակապես անսխալական ճանապարհ է: Սկսելով առաջադրված խնդրից՝ կազմում ենք խնդիրների շղթա, որոնցից յուրաքանչյուրը համարժեք է լուծմանը և ավելի մոտ է նրան, քան նախորդը. այս կերպ անցնելով խնդրից խնդիր՝ վերջին քայլով հասնում ենք լուծմանը:

Սակայն նույնիսկ մաթեմատիկայում անհայտը փնտրելու կամ ապացույցի փորձերում հաճախ ենք հանդիպում նրան, ինչը կարելի է ոչ լրիվ բավարարվածություն անվանել: Այդ պատճառով էլ կդիտարկենք օժանդակ խնդիրների ուրիշ տեսակներ:

§ 4. Ավելի կամ պակաս արդյունավետ օժանդակ խնդիրներ. միակողմանի ռեդուկցիա

Սկսենք սխեմատիկ խնդիր դիտարկելուց.

Ա. Գտեք բուրգի ծավալը, եթե տրված են...

Համարենք, որ ծավալը հաշվելու համար բավարար տվյալներ են նշված, բայց դրանց մեջ չկան ո՛չ բուրգի հիմքի մակերեսը, ո՛չ էլ բուրգի բարձրությունը. այդ մեծություններից ոչ մեկը տրված չէ: Մեզ համար սա շատ կարևոր է, թե իրենցից ինչ են ներկայացնում տվյալները այլ իմաստով. այստեղ մեզ չի հետաքրքրի, և այդ պատճառով էլ դրանց մասին լռում ենք:

Հայտնի է, որ բուրգ ծավալը կարելի է հաշվել, եթե տրված են հիմքի մակերեսը և բուրգի բարձրությունը, սակայն, ինչպես հենց նոր ասացինք, այդ մեծություններից ոչ մեկը տրված չէ: Քանի որ այդ մեծությունները մեզ հայտնի չեն, կփորձենք դրանք հաշվել. և այսպես, մեր առջև նոր խնդիր է կանգնում.

Բ. Գտեք բուրգի բարձրությունը և հիմքի մակերեսը, եթե տրված են....

Ա խնդրում մեկ անհայտ ունեինք, Բ-ում՝ երկու, երկու խնդիրներում էլ տվյալները նույնն են (դրանք չեն նշել): Կարելի է ասել, որ մեր խնդիրների  միջև կապը միակողմանի է, անհամաչափ: Եթե կարողանանք լուծել Բ խնդիրը, մեզ հայտնի կդառնան բուրգի բարձրությունը և հիմքի մակերեսը, և հետևաբար կկարողանանք հաշվել նրա ծավալը, այսինքն՝ լուծել Ա խնդիրը: Բայց, եթե կարողանում ենք լուծել Ա խնդիրը, դա դեռ չի նշանակում, որ կարող ենք լուծել նաև Բ խնդիրը. չնայած որ Ա խնդրի արդյունքից հետևում է Բ խնդրում եղած  երկու անհայտների միջև պարզ առնչություն, դրանցից յուրաքանչյուրի առանձին որոշելը կարող է լուրջ դժվարությունների հանդիպել: Այսպիսով, Ա-ն լուծելով՝ ավելի քիչ բանի ենք հասնում, քան Բ-ն լուծելով: Ա և Բ խնդիրներից Ա-ն կարելի է անվանել պակաս արդյունավետ, իսկ Բ-ն ավելի արդյունավետ:

Ունենք չլուծված երկու խնդիր՝ Ա և Բ, որոնց մասին միայն կարող ենք պնդել՝ մեզ հայտնի է, թե ինչպես կարող ենք Բ խնդրի լուծումից ստանալ Ա խնդրի լուծումը, բայց մեզ անհայտ է, թե ինչպես կարող ենք Ա խնդրի լուծումից ստանալ Բ խնդրի լուծումը: Այդ դեպքում ասում ենք, որ Ա-ն պակաս արդյունավետ է, քան Բ-ն, կամ (ինչը նույնն է) Բ-ն ավելի արդյունավետ է, քան Ա-ն:

Անցումը սկզբնական խնդրից օժանդակին՝ ավելի կամ պակաս արդյունավետի, քան սկզբնականը (համենայնդեպս՝ ոչ համարժեք), անվանում են միակողմանի (կամ անշրջելի) ռեդուկցիա: Մեր օրինակում սկզբնական Ա խնդիրը պակաս արդյունավետ էր, քան Բ-ն, և այդ պատճառով Ա-ից Բ ռեդուկցիան միակողմանի է: Խորագիտակ ընթերցողը հավանաբար կարող է շատ օրինակներ հիշել, մերի նմանակ, որոնցում միակողմանի ռեդուկցիան օգտակար է:

Հաճախ միակողմանի ռեդուկցիան օգտակար է լինում նաև հակառակ ուղղությամբ, այսինքն՝ ռեդուկցիա, որտեղ օժանդակ խնդիրը պակաս արդյունավետ է, քան սկզբնականը: Ահա սխեմատիկ օրինակ.

Ա. Հաշվեք x₁, x₂, ...x_n-1, x_n անհայտները, եթե տրված են....
Բ. Գտեք x₁ անհայտը, եթե տրված են...

Ենթադրում ենք, որ տվյալները և պայմանները բավարար են անհայտները գտնելու համար և երկու խնդրում էլ դրանք նույնն են, բայց հիմա դրանք ոչ մի դեր չեն խաղում, և այդ պատճառով էլ դրանց մասին լռում ենք: Որ Ա խնդրի լուծումը միաժամանակ նշանակում է Բ խնդրի լուծումը, ակնհայտ է, սակայն, ընդհանուր առմամբ, չի կարելի պնդել, որ լուծելով Բ խնդիրը, դրանով լուծել ենք նաև Ա խնդիրը. մեր սահմանման համաձայն Ա-ն ավելի արդյունավետ է, քան Բ-ն: Այնուամենայնիվ, շատ հաճախ Ա խնդիրը լուծելիս կարելի Բ-ն օգտագործել որպես օժանդակ խնդիր. այդպես շատ անգամ ենք արել գլուխ 3-ում, երբ Ա խնդիրը անդրադարձ մեթոդով լուծելիս x₁-ը ընտրել ենք որպես անհայտ, որը պետք է մյուսներից ավելի շուտ գտնել, և մեր աշխատանքը սկսել ենք օժանդակ Բ խնդրից՝ այն դիտելով որպես Ա խնդրի լուծման բանալի:

§ 5. Անուղղակի օժանդակ խնդիրներ

Օրինակից սկսենք: Դիտարկենք այսպիսի խնդիր.

Ա. Գտեք կանոնավոր քառանիստին արտագծած գնդոլորտի շառավիղը՝ իմանալով քառանիստի կողի երկարությունը:

Եթե չի հաջողվում ինչ-որ մոտեցում գտնել Ա խնդրին, կարելի է փորձել լուծել հետևյալ օժանդակ խնդիրը.

Բ. Գտեք հավասարակողմ եռանկյանն արտագծած շրջանագծի շառավիղը՝ իմանալով եռանկյան կողմի երկարությունը:

Ա-ից Բ անցումը չի լինի ո՛չ միակողմանի, ո՛չ երկկողմանի ռեդուկցիա՝ § 2-ում և §4-ում սահմանված իմաստով: Իսկապես, հազիվ թե կարելի է  a priori նկատել, թե ինչպես Բ խնդրի լուծումից կարելի ստանալ Ա խնդրի լուծումը կամ, հակառակը, Ա խնդրի լուծումից ստանալ Բ խնդրի լուծումը. Ա և Բ խնդիրները համարժեք չեն թվում, դրանցից ոչ մեկը, մեր սահմանած իմաստով, ավելի արդյունավետ չէ, քան մյուսը:

Համենայն դեպս Ա և Բ խնդիրներն ազգական են: Բ խնդիրը «նմանակ» է Ա խնդրին. այստեղ հանդիպում ենք օրինակներից մեկին, որոնք վկայում են հարթաչափության և տարածաչափության միջև եղած խորը նմանակության մասին: Եվ, իհարկե, մեզանից շատերին Բ խնդիրը ավելի հեշտ կթվա Ա խնդրից. հնարավոր է նույնիսկ, որ արդեն ինչ-որ ժամանակ հանդիպել ենք Բ խնդրին և առանց դժվարության կարող ենք հիշել, թե ինչպես ենք լուծել: Նման իրավիճակում բնական հարց է առաջանում՝ արժե՞ զբաղվել Բ խնդրով: Հույս կա՞, որ Բ խնդրի ուսումնասիրությունը կհեշտացնի Ա խնդրի լուծումը:

Հնարավոր է, որ Բ խնդրի ուսումնասիրությունը ոչ մի արժեքավոր բան չտա Ա խնդիրը լուծելու համար՝ այդպիսի իրավիճակի կարող ենք հանդիպել նույնիսկ այն դեպքում, երբ Ա և Բ խնդիրների միջև նմանակումը բացարձակապես ակնհայտ է, և Բ խնդրի լուծումը ամբողջությամբ մեզ հայտնի է: Բայց կարող է նաև պարզվի, որ Բ խնդրի լուծումը օգտակար է, չնայած առաջին հայացքից այդ խնդիրը մեզ անպտուղ է թվում: Ա խնդրի համեմատումը իր նմանակ Բ խնդրի հետ կարող է Ա խնդիրը ավելի ուսանելի դարձնել, և այդ դեպքում Բ խնդիրը օգտակար կլինի: Բ խնդիր լուծման ներդրումը Ա խնդրի լուծման գործում հաճախ այնքան էլ անմիջական չի լինում. օրինակ, բացառված չէ, որ Ա և Բ խնդիրների նմանակումը մեզ մոտ ինչ-որ օգատակար միտք առաջացնի: Այսպես, ասենք, Բ «հարթ» խնդրի դեպքում որոնելի շառավիղը հավասար է հավասարակողմ եռանկյան բարձրության որոշակի ոչ բարդ ռացիոնալ պատիկին (բարձրության 2/3-ին): Սա կարող է հարց առաջացնել՝ իսկ ինչպե՞ս կլինի «տարածական» Ա խնդրի դեպքում: Կարտահայտվի՞ որոնելի շառավիղը կանոնավոր քառանիստի բարձրության ինչ-որ ռացիոնալ մասով: Այս և նման հարցերը կարող են բավականին արդյունավետ լինել և Ա խնդիրը լուծելու ճանապարհ բացել: Նաև հնարավոր է, որ Ա խնդիրը լուծելիս մեզ պետք լինի հաշվել քառանիստի նիստերից մեկին արտագծած շրջանագծի շառավիղը (օրինակ, քառանիստի բարձրությունը հաշվելու համար, որի քառակուսին, ակնհայտորեն, հավասար է քառանիստի կողի քառակուսու և նիստին արտագծած շրջանագծի շառավղի քառակուսու տարբերությանը). այս դեպքում Բ խնդիրը լուծել կարողանալը կարող է շղթայի մի օղակը լինել, որը պետք է կռենք Ա խնդրի լուծումը ստանալու համար:

Ընդհանրապես կարելի է սպասել, որ Բ խնդրի ուսումնասիրությունը կբերի այս կան այն ներդրումը սկզբնական Ա խնդրի լուծման հարցում, նույնիսկ այն դեպքում, երբ Բ-ն ոչ համարժեք է Ա-ին, ոչ ավելի արգասաբեր է, քան Ա-ն, ոչ պակաս արգասաբեր, քան Ա-ն: Այսպիսի խնդիրը կոչվում է Ա-ի նկատմամբ կողմնակի օժանադակ խնդիր:

§ 6. Մասնակի օգնություն, մեթոդոլոգիական օգնություն, խթանում, ղեկավարում, փորձառություն

Օժանդակ խնդիրը անթիվ ձևերով կարող է օգնել սկզբնական խնդիրը լուծել:

Սկզբնականին համարժեք խնդիրը, եթե նրա լուծումը գտել ենք, ապահովում է սկզբնական խնդրի ամբողջական լուծումը. սա ճիշտ է նաև օժանդակ խնդրի համար, որը ավելի արգասավոր է, քան սկզբնականը: (Օժանդակ խնդիրների այս երկու տեսակների տարբերությունը պարզ երևում է նույնիսկ այն ժամանակ, երբ օժանդակ խնդիրը չենք կարողանում լուծել: Եթե համարժեք խնդրի լուծումը անհասանելի է, դա ճիշտ կլինի նաև սկզբնական խնդրի համար. եթե անհասանելի է ավելի արդյունավետ խնդրի լուծումը, սկզբնական խնդիրը լուծելու հեռանկարը այդքան մռայլ չպետք է համարենք):

Օժանդակ խնդիրների որոշ տեսակներ, նույնիսկ եթե հաջողվում է լուծել, չեն երաշխավորում սկզբնական խնդրի լուծումը. սակայն նրանք կարող են մասնակի օգնություն ցուցաբերել խնդիրը լուծելու հարցում: Օժանդակ խնդրի լուծման մասը (կամ նույնիսկ լուծումը ամբողջությամբ) կարող է լինել սկզբնական խնդրի լուծման մասը, վերջինի համար ապահովելով ինչ-որ եզրակացություն, կառուցում (կամ ուղղակի առանձին փաստ, որը կծառայի այդպիսի եզրակացության, կառուցման և այլն համար հիմք):

Նույնիսկ եթե մի տեղ չկա, որտեղից այդպիսի մասնակի օգնությունը հայտնվի, օժանդակ խնդիրը կարող է մեթոդոլոգիական օգնություն տալ. կարող է հուշել լուծման մեթոդը, նշել լուծման ընդհանուր ուրվագիծը կամ ուղղությունը, որ ուղղությամբ պետք է սկսել աշխատանքը, և այլն: Տրվածին նմանակ, բայց ավելի հեշտ օժանդակ խնդիրը (համեմատիր §5-ում քննարկված օրինակը) շատ հարմար է այդպիսի մեթոդոլոգիական օգնության համար:

Հնարավոր է, որ երբեմն չենք կարողանա սկզբնական խնդրի վերջնական լուծման մեջ առանձնացնել այն մասը կամ միտքը, որը փոխառված էր ինչ-որ օժանդակ խնդրից կամ նրանից էր հուշված: Ամեն դեպքում շատ հավանական է, որ այդ օժանդակ խնդրի խթանող ազդեցությունը արժանի ներդրում է արել սկզբնական խնդրի լուծումը փնտրելու հարցում: Հնարավոր է, որ օժանդակ խնդիրը իր նմանությամբ կամ հակադրությամբ սկզբնական խնդիրը ավելի հասկանալի, ավելի մատչելի դարձրեց. կամ այն կենդանացրեց մեր հիշողությունը՝ շարժման մեջ դրեց մեր մտքերի շարանը, որոնցից առաջացան դիտարկվող խնդրի լուծման հետ կապ ունեցող մի քանի էական փաստեր:   

Օժանդակ խնդիրները բավականին նուրբ մի ձևով էլ կարող են օգնել: Խնդրով զբաղվելով՝ հայտնի որոշումներ ենք կայացնում: Ենթադրենք, որ աշխատանքը կարող ենք երկու ուղղությամբ շարունակել, որ մեր առջև երկու ուղի կա՝ մեկը դեպի աջ, մյուսը՝ ձախ: Դրանցից ո՞րն ընտրենք: Ավելի հավանական է՝ ո՞րը կհասցնի լուծման: Պետք է կարողանալ խելամիտ գնահատել հնարավորությունները՝ և այստեղ էլ  օժանդակ խնդիրները կարող են ցանկալի ուղեցույց լինել: Շատ հավանական է, որ օժանդակ խնդրի վրա ծախսած ուշադրությունը և աշխատանքը, և այդ ընթացքում ձեռք բերած փորձը շատ բարենպաստ ազդեն սկզբնական խնդրի լուծման վրա:

Երբեմն օժանդակ խնդիրներով կարող ենք զբաղվել ուղղակի փորձառության համար: Պատահում է, որ սկզբնական խնդիրը գաղափարներ է պարունակում, որոնց հետ աշխատելուն վարժված չենք: Նման վիճակում կարելի առաջարկել ավելի հեշտ խնդիր փորձել լուծել, որը նույն գաղափարներն է պարունակում. այդ դեպքում վերջին խնդիրը դառնում է (բավականին հեռու) օժանդակ խնդիր մեր սկզբնական խնդրի համար:

Չնայած այսքան շատ բարենպաստ հնարավորությունների գոյությանը, հաճախ է պատահում, որ շատ քիչ ենք շահում, իսկ օժանդակ խնդրի վրա իզուր շատ ենք ժամանակ ու աշխատանք ծախսել: Այդ պատճառով էլ, քանի դեռ շատ չենք խորացել օժանդակ խնդրում, արժի փորձել կշռադատել և գնահատել բոլոր հնարավորությունները:

Գլուխ 9-ի վերաբերյալ լրացուցիչ վարժություններ և ծանոթություններ

1. Օժանդակ խնդիրների հուսալի աղբյուրնե՞ր: Օժանդակ խնդիրը կարող է «ինքնաբուխ ծնվել» սկզբնական խնդրից: Բայց կարող է նաև մեզ գրավի օժանդակ խնդրի անցնելու միտքը (բավականին հեռանկարային), բայց մտքներիս ոչ մի բան չգա: Նման իրավիճակներում ցանկալի կլիներ ունենալ աղբյուրների ցանկը, որտեղից կարելի է օգտակար օժանդակ խնդիրներ վերցնել: Գործնականում շատ ստանդարտ հնարքներ կան օժանդակ խնդիրներ կազմելու համար, և հետագայում կդիտարկենք դրանցից առավել ակնհայտները. շատ դեպքերում դրանք բերում են որոշակի օժանդակ խնդիրների, բայց առանց երաշխավորությունների, որ այդ խնդիրները անպայման օգտակար կլինեն:
   Օժանդակ խնդիրը կարող է ծնվել լուծման պրոցեսի ցանկացած փուլում: Սակայն կհամարենք, որ շատ չենք հեռացել անենասկզբնական փուլից: Արդեն դիտարկվել և լավ ուսումնասիրվել են խնդրի գլխավոր տարրերը՝ անհայտները, տվյալները և պայմանները, կամ նախադրյալները և եզրակացությունները, ինչպես նաև ակնհայտ ստորաբաժանումները («կետերը», պայմանները և այլն): Բայց առայժմ հուսալի ծրագիր չի երևում, և  կուզենայինք ունենալ առավել մատչելի և առավել գրավիչ նպատակ: Նման իրավիճակներում լավ է վստահություն ունենալը, որ խնդրի գլխավոր տարրերի ուսումնասիրությունը կարող է մեզ այդպիսի նպատակ տալ, որը կհայտնվի համապատասխան օժանդակ խնդրի հետ միասին: Հիմա դիտարկենք առավել դիտարժան դեպքերը:
    
2. Respice finem. Նպատակին հասնելու ձգտումը կարելի է դիտարկել որպես գործողություններ հուշող խթան, որոնք, հնարավոր է, կհասցնեն նպատակին: Այդ պատճառով էլ նայեք վերջին, նպատակից հայացքը մի՛ շեղեք, այն ուղղորդում է ձեր մտքերը: Respice finem նշանկում է «Նայիր վերջին». այս արտահայտությունը գործածական էր, երբ լատիներենը ընդհանուր գործածական էր: Գոբսը բացատրում է. «…ձեր բոլոր գործողություններում հաճախ աչքի առաջ ունեցեք այն, ինչին ուզում եք հասնել, որպես առարկա, որն ուղղորդում է ձեր միտքը դրան հասնելու ճանապարհին»:
   Մտորելով խնդրի վերջի մասին՝ հուսով ենք, որ դրա լուծման համար հարմար միջոցների մասին միտք է առաջանում: Որպեսզի այդ մտքի հայտնվելու համար անհրաժեշտ ժամանակը կրճատենք, պետք է ձգտել վերջը պատկերացնել առավելագույն հստակությամբ. Ի՞նչ է պահանջվում: Ի՞նչ սեռի օբյեկտ եք ուզում գտնել: Ի՞նչh է անհայտ: Ո՞րն է եզրակացությունը: Պետք է ամենահամառ ճիգեր գործադրենք, որպեսզի մեր երևակայությունում համապատսխան միջոցներ առաջացնենք. Ինպե՞ս կարելի է նման օբյեկտ ստանալ: Որտե՞ղ կարելի է նման օբյեկտ գտնել: Ո՞ր խանութում կարող ենք նման իր ձեռք բերել: Ինչպե՞ս կարելի նման անհայտը գտնել: Ինչպե՞ս կարելի է նման եզրակացություն անել:
   Վերջին երկու հարցը հատկապես մաթեմատիկական խնդիրներին են վերաբերում՝ մեկը որոնման խնդիրներին, մյուսը՝ ապացուցման: Այդ դեպքերը առանձին-առանձին դիտարկենք:

1° Որոշման խնդիրներ. Ինչպես արդեն արել ենք § 4-ում, դիտարկենք սխեմատիկ խնդիր. «գտեք բուրգի ծավալը, եթե տրված են…»: Այս խնդրում անհայտը կոնկրետ նշված է, մինչդեռ պայմանները և տվյալները ճշտված չեն: Ինչպե՞ս կարելի է գտնել այդպիսի անհայտը: Ինչպե՞ս կարելի է հաշվել բուրգի ծավալը: Ի՞նչ տվյալներ են պետք այդպիսի անհայտը գտնելու համար: Մեզ առաջադրված խնդրում տվյալները, իհարկե, բավարար են, բայց դժբախտություն է, գոնե այս պահին, որ այդ տվյալներից անհայտը ստանալ չենք կարողանում: Էականում, կցանկանայինք հարմար տվյալներ ունենալ. իրականում կցանկանայինք գործ ունենալ նույն անհայտը ունեցող ուրիշ, ավելի մատչելի խնդրի հետ:
Եթե հաջողվում է այդպիսի խնդիր գտնել, կարող են տարբեր իրավիճակներ հանդիպել:
2°. Նույն անհայտը ունեցող նախօրոք լուծված խնդիրներ: Եթե բախտներդ այնքան է բերել, որ հիշել եք այդպիսի խնդիր, դրա տվյալները կարելի է դիտարկել որպես օժանդակ խնդրի անհայտներ և դրանով առաջ շարժվել մեր հիմնական խնդրի լուծման հարցում: Այդպիսի ընթացակարգը հաճախ օգտակար է լինում: Դա ցուցադրենք մեր (հենց նոր հիշատակված, սխեմատիկ) օրինակի վրա:
Այս խնդրում անհայտը բուրգի V ծավալն է: Ամենատարածված խնդրում այդպիսի անհայտի հետ տրվում են հիմքի S մակերեսը և բուրգի h բարձրությունը: Մենք գիտեինք այս խնդրի լուծումը՝ V=Sh/3, և մեզ հաջողվեց հիշել այն: Ինչպե՞ս օգտագործենք այս լուծումը: Բնական է փորձել հաշվել S-ը և h-ը սկզբնական խնդրի (չլուծված) տվյալների օգնությամբ: Փորձելով դա անել, S-ը և h-ը ընդունում ենք որպես նոր անհայտներ. այդպիսով երկու նոր խնդիր ենք ներմուծում, որոնցից մեկում անհայտը S-ն է, իսկ մյուսում՝ h-ը. այս խնդիրների տվյալները համընկնում են հիմնական խնդրի տվյալների հետ: (Այս կոնկրետ դեպքը դիտարկված է 4-րդ գլխի 18 և 19 վարժություններում):
3° Նշված ընթացակարգից շատ հաճախ են օգտվում, և շատ դեպքերում հարկ է լինում կրկին կիրառել:
Դիցուք x-ով նշանակել են մեզ առաջադրված ելման խնդրի սկզբնական անհայտը: Ձգտում ենք հարմար տվյալներ գտնել և նկատում ենք, որ կկարողանայինք գտնել x-ը, եթե իմանայինք y', y'', y''', .... (ընթացքում օգտագործելով նախօրոք լուծված խնդրի լուծումը): Մենք դիտարկում ենք y', y'', y''', .... որպես նոր նպատակներ, որպես երկրորդական անհայտներ: Այնուհետև, կկարողանայինք գտնել у', у", у'", ...., եթե իմանայինք z, z', z'', .... (օգտագործելով նախօրոք լուծված մի քանի խնդիրների լուծումներ), և նորից դիտարկում ենք z, z', z'', .... որպես նոր նպատակներ, որպես երրորդ կարգի անհայտներ, և այլն: Շարժվում ենք վերջից դեպի սկիզբը (տես գլուխ 8-ի § 2-ը):
Որպեսզի լավ պատրաստվենք այդպիսի աշխատանք կատարելուն, պետք է խնդիրների պահուստ ունենանք (հաճախակի օգտագործվող, հիմնական) և այդ պահուստը պետք է լավ ընտրված և լավ համակարգված լինի (տե՛ս գլուխ 12-ի 4 –րդ վարժությունը):
4°. Նույն անհայտով չլուծված խնդիր: Այդպիսի խնդիրը կարելի է դիտարկել որպես սկզբնական խնդրի լուծման բանալի: Մենք ձեռնամուխ ենք լինում այդ խնդրին, որպես օժանդակ խնդրի, և ձգտում ենք այն լուծել. այսպիսի ընթացակարգը կարող է օգտակար լինել: Սակայն, այլ հավասար պայմանների դեպքում, այստեղ հեռանկարները պակաս բարենպաստ են, քան 2°-ի դեպքում: Իսկապես, որպեսզի այդպիսի օժանդակ խնդրից առավել բնական ճանապարհով օգուտ քաղենք, սկզբում պետք է այն լուծել, իսկ հետո ի լրումն պետք է դեռ կարողանալ այն կիրառել, ինչպես նկարագրված է 2° կետում:
5°. Եթե ընդհանրապես պարզ չէ, թե ինչպես կարելի է օգտագործել անհայտը, որը տրված է դիտարկվող խնդրում, եթե չենք կարողանում հիշել նույն անհայտով նախապես լուծված խնդիր կամ նորը հորինում, որը կկարողանայինք լուծել, ապա պետք է փորձենք գտնել մոտիկ անհայտով խնդիրներ: Այսպես, օրինակ, եթե պահանջվում է հաշվել բուրգի ծավալը, և ուրիշ ճանապարհ չի երևում, կարելի է փորձել հիշել, թե ինչպես ենք գտել եռանկյան մակերեսը՝ օգտագործելով տարբեր մոտեցումներ և ձգտելով եռանկյան և եռանկյուն բուրգի (քառանիստի) միջև նմանակումից ինչ-որ ուղղորդող դատողություններ գտնել:
6°. Ապացուցման խնդիրներ: Այստեղ կարող էինք փոքր փոփոխություններով կրկնել ամենը, ինչ ասվեց որոնման խնդիրների մասին, բայց թռուցիկ ակնարկն էլ բավական է:
Այս դեպքում էլ սխեմատիկ օրինակից սկսելը հարմար է: Դիցուք՝ պահանջվում է ապացուցել այսպիսի թեորեմ. «Եթե...., ապա անկյունը ուղիղ է»: Այս թեորեմի եզրակացությունը կոնկրետ ձևակերպված է՝ «անկյունն ուղիղ է», բայց պայմանները որոշակի չեն: Նման եզրակցությունն ինչպե՞ս կարելի է ապացուցել: Ի՞նչ պայմանից կբխի այդպիսի եզրակացություն: Այս հարցերը մեզ հուշում են նման եզրակացությամբ թեորեմ փնտրել, որի պնդումը՝ «անկյունն ուղիղ է» բխում է ինչ-որ ուրիշ պայմանից, որը ավելի հեշտ կարող ենք հաղթահարել:
Եթե բախտներս բերի և հիշենք նման եզրակացությամբ արդեն ապացուցված թեորեմ, կարող ենք նրա պայմանը ընդունել որպես միջանկյալ նպատակ, այսինքն՝ փորձենք մտաբերած թեորեմի պայմանները ապացուցել՝ ելնելով այն թեորեմի պայմաններից, որը պետք է ապացուցեինք:
Նման ընթացակարգը բավականին հաճախակի է հաջողում: Շատ դեպքերում կարելի է կրկին կիրառել և, շարժվելով վերջից դեպի սկիզբը, գտնել պահանջվող եզրակացության ապացույցը:
Եթե հաջողվում է հիշել նույն եզրակցությամբ թեորեմ, ինչ առաջադրվածը, բայց դեռ չապացուցված, կարելի է փորձել սկզբում դա ապացուցել: Նման փորձը կարող է օգուտ բերել, բայց պետք է մանրամասնորեն կշռադատել հեռանկարը:
Եթե մեզ չհաջողվի հիշել նույն եզրակցությունն ունեցող և նախօրոք ապացուցված թեորեմ կամ մտածել ինչ-որ նոր թեորեմ, որը կկարողանայինք ապացուցել, կարելի է փորձել գտնել նմանակերպ եզրակացություն ունեցող թեորեմ:
7°. Ինչպիսին էլ որ լինի մեր խնդիրը, կարելի է նախօրոք վստահ լինել, որ այն լուծելիս հարկ կլինի կիրառել նախօրոք ձեռք բերած գիտելիքները: Բայց չենք կարող նույն վստահությամբ կանխատեսել, թե գիտելիքի ո՛ր բաժիններն անհրաժեշտ կլինեն, հատկապես, եթե խնդիրը դժվար է: Ընդհանուր առմամբ, նախօրոք լուծած ցանկացած խնդիր կամ երբևէ ապացուցած թեորեմ կարող են օգտակար լինել, հատկապես, եթե շփման կետեր ունեն դիտարկվող խնդրի հետ, բայց այդ բոլոր խնդիրները և թեորեմները ուսումնասիրելու ժամանակը չունենք: Նախորդ դատողությունները մեր ուշադրությունը ուղղորդում են հպման ամենահավանական կետերին: Որոշման խնդրի դեպքում առավել հավանական է, որ օգտակար լինի նույն սեռի անհայտ ունեցող խնդիրը, որը նախօրոք լուծել ենք, ապացուցման խնդրի դեպքում՝ նույն եզրակացությունն ունեցող խնդիրը: Այդ պատճառով էլ պետք է անպայման առաջնություն տալ այսպիսի հարցերին՝ ինչպե՞ս կարելի է գտնել նման անհայտը. ինչպե՞ս կարելի է ապացուցել այսպիսի եզրակցությունը:

3. Պայմանում կետ ավելացնելը կամ պակասեցնելը: Երբ մեր աշխատանքը դանդաղ է առաջ գնում կամ ընդհանրապես չի շարժվում, սկսում ենք կորցնել համբերությունը և ձգտում ենք ուրիշ խնդրի անցնել: Այդ պահին լավ է ծանոթ լինել սկզբնական խնդրի վերափոխումների, որոնք հանգեցնում են մոտիկ խնդիրների, որոնց ուսումնասիրությունը կարող է օգտակար լինել հիմնական խնդիրը լուծելու համար: Թվարկենք այդպիսի վերափոխումներից առավել ակնհայտները:

Որոշման խնդիրներ

1°. Խնդրի պայմանում որոշակի վերապահում անտեսելը:
2°. Պայմանում վերապահում ավելացնելը:
Առաջին փոփոխությունը պայմանը ընդարձակում է, երկորդը՝ նեղացնում է:

Ապացուցման խնդիրներ

1°. Պայմանում ինչ-որ  ենթադրություն անտեսելը:
2°. Պայմանում ինչ-որ ենթադրություն ավելացնելը:
3°. Եզրակացության մեջ ինչ-որ պնդում անտեսելը:
4°. Եզրակացության մեջ ինչ-որ պնդում ավելացնելը:
Առաջին և չորրորդ փոփոխությունները խստացնում են թեորեմը. երկրորդ և երրորդ փոփոխությունները՝ թուլացնում:
Այս փոփոխությունների ազդեցությունը դիտարկված է 4 և 5 լրացուցիչ դիտողություններում:

4. Պայմանի ընդարձակելը կամ նեղացնելը: Դիտարկենք նույն խմբին պատկանող երկու՝ A(x) և B(x) պայմաններ, որոնք պարունակում են նուն x օբյեկտը: Կասենք  A(x)-ը նեղ է B(x)-ից, կամ (ինչը նույնն է) B(x)-ը լայն է A(x)-ից, եթե A(x)-ի բավարարող ցանկացած օբյեկտ բավարարում է նաև B(x)-ին: (Այսպիսով, այս տերմինները օգտագործում ենք «ոչ խիստ» իմաստով. երբ A(x) և B(x) պայմանները հավասարազոր են, կարող ենք ասել, որ A(x)-ը ավելի նեղ է B(x)-ից և որ B(x)-ը նեղ է A(x)-ից):

1°. Պայմանի ընդարձակելը նշանակում է սկզբնական խնդրից անցնել մեկ ուրիշ՝ ավելի լայն պայմանով խնդրի: Ընթերցողը գիտի, որ նախորդ գլուխներում հաճախ ենք նման անցում արել (չնայած և չենք նկարագրել այդպիսի արտահայտություններով): Այսպես, օրինակ, երկրաչափության կառուցման խնդրի պայմանում (համապատասխան ձևով ձևակերպված) սովորաբար խոսքը կետի մասին է լինում: Երկրաչափական տեղը, որին պատկանում է կետը, ստանում ենք, պահելով միայն պայմանի մի մասը և անտեսելով մնացածը, այսինքն՝ ընդարձակելով պայմանը: Ահա ևս մեկ օրինակ. մի քանի անհայտները գտնելու համար անհրաժեշտ հավասարումների համակարգից սկզբում կազմելով միայն հավասարումներից մեկը՝ ամբողջ պայմանից ուշադրության ենք առնում միայն մի մասը (պահանջ, կետ, դիտողություն...) և, այսպիսով, ըստ էության, պայմանը ընդարձակում ենք:
Պայմանը ընդարձակելը հատկապես օգտակար է, եթե հաջողվում է երկու պահանջ կատարել.
ա) գտնել (նկարագրել, թվարկել...) բոլոր օբյեկտների հավաքածուն, որոնք կբավարարեն ընդարձակված պայմանին.
բ) այդ հավաքածուից հեռացնել այն օբյեկտները, որոնք բավարարում են սկզբնական պայմանին:
Կարծում եմ, որ ընթեցողին հայտնի է, թե այդ երկու նպատակներին ինչպես են հասնում երկրաչափական տեղերի մեթոդով. այստեղ օգտակար է մի անգամ էլ նայել գլուխ 6-ի §3-ի կետ 3-ը և գլուխկոտրուկներին վերաբերող որոշ վարժություններ և դիտողություններ (տես նաև գլուխ 6-ի վարժություն 23-ը):
Ընդարձակված պայմանը կարելի է ուրիշ կերպ օգտագործել, ինչպես հեշտությամբ կնկատի ըներցողը, ով արդեն ծանոթ է Դեկարտի ծրագրի հետ:
2°. Պայմանը նեղացնելը նշանակում է սկզբնական խնդրից անցում կատարել ավելի նեղ պայմանով ուրիշ խնդրի: Թեմատիկան, որին մինչև հիմա հիմնականում դիմել ենք, այնքան էլ շատ հնարավորություն չի տալիս այս ընթացակարգը կիրառելու: Սակայն, ահա այդպիսի մի օրինակ:
Դիցուք՝ պահանջվում է լուծել a₁, a₂, ..., a_n ամբողջ գործակիցներով n-րդ աստիճանի հավասարումը՝ Xⁿ+a₁x^n-1+ a₂x^n-2+ a_{n =} 0։
Սկզբում նպատակահարմար է տեսնելը, թե ունի՞ ամբողջ արմատներ: Լրացուցիչ պահանջ ներկայացնելով, որ x-ը ամբողջ թիվ լինի, ըստ էության, նեղացնում ենք խնդրի պայմանը: Բայց ամբողջ արմատներ փնտրելը համեմատաբար հեշտ է (դրանք պետք է լինեն a_n ազատ անդամի բաժանարարները), և եթե հաջողվի գոնե մեկ արմատ գտնել, կկարողանանք հավասարման աստիճանը իջեցնել, դրանով հեշտացնելով մյուս արմատների որոնումը: (Կոնկրետ օրինակ է տրված 2 գլխի 32 վարժությունում):
Պայմանների նեղացնելը հաճախ կարող է օգտակար լինել և ավելի խորը խնդիրներ դիտարկելիս (տես 11 վարժությունը):

5. Ավելի խիստ կամ ավելի թույլ թեորեմ դիտարկելը: Երկու՝ A և B պնդում դիտարկենք: Եթե հայտնի է, որ A-ն հետևում է B-ից (այսինքն, եթե կարող ենք արտածել, որ A-ն ճշմարիտ է՝ ենթադրելով, որ B-ն ճշմարիտ է), կասենք, որ A-ն ավելի թույլ է B-ից, կամ (ինչը նույնն է) B-ն ուժեղ է A-ից: A-ի և B-ի միջև այս առնչությունը հատկապես հետաքրքիր է դառնում, երբ ո՛չ կարողանում ենք ապացուցել, ո՛չ էլ հերքել այդ պնդումներից որևէ մեկը:

1°. Ապացույցի հնարավոր հենքի ուսումնասիրությունը: Դիցուք ցանկանում ենք ապացուցել, որ ինչ-որ երկու մեծություններ հավասար չեն միմյանց: Ենթադրենք, օրինակ, պատրաստվում ենք ապացուցել A թեորեմը, որը պնդում է, որ ։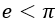
Դժվար չէ նկատելը, որ կա մի երրորդ մեծություն, որի հետ հարմար է համեմատել տրված երկուսը: Մեր դեպքում ինչպես e-ն, այնպես էլ 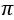 –ն հեշտ է համեմատել 3-ի հետ: Այդ պատճառով էլ A թեորեմը ապացուցելու համար, դիտարկենք B թեորեմը, որը պնդում է, որ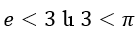 
Պարզ է, որ A-ն անմիջապես հետևում է B-ից: Մեր նոր՝ B պնդումը ավելին է հաստատում, քան A-ն է, և այդ պատճառով այն ավելի խիստ է, քան A պնդումը, որը սկզբում պատրաստվում էինք ապացուցել:
Ընդհանրապես նշենք, որ երկու իռացիոնալ թվերի միջև անհավասարություն ապացուցելիս, միշտ ստիպված ենք լինում գործել ինչպես հենց նոր դիտարկած օրինակում, այսինքն՝ միշտ ստիպված ենք լինում փնտրել ինչ-որ ռացիոնալ թիվ, որը այդ երկու իռացիոնալ թվերը առանձնացնում է: Նման ձևով վարվելով՝ սկզբնական պնդումը հանգեցնում ենք ավելի ուժեղի, ինչպես մեր օրինակում էր. առանձնացնող թվի օգտագործելը բերում է ավելի ուժեղ պնդումի:
Ավելի լուրջ հետազոտություններում նման իրավիճակներ բավականին հաճախ են հանդիպում, և սկզբնական A թեորեմը ապացուցելու համար ստիպված ենք լինում հորինել ավելի ուժեղ B թեորեմ, որից հետևում է A-ն, և որը, հանգամանքներից ելնելով, ավելի հեշտ է ապացուցելը, քան A թեորեմը: Ապացուցելով B-ն, կարծես մերկացնում ենք A թեորեմի ճշմարիտ լինելու «հիմքում» ընկած փաստը: Իհարկե, երբ հորինում ենք B թեորեմը, որից պետք է հետևեր A թեորեմը, դեռ չգիտենք, թե կարող ենք այն ապացուցել, դեռ ավելին, նույնիսկ չգիտենք՝ ճշմարի՞տ է B թեորեմը: Այսպիսով, այս պահին B թեորեմը դեռևս սկզբնական թեորեմի համար «հիմք» չէ, այլ միայն «հնարավոր հիմք»: Եվ ամեն դեպքում, կարելի է B-ի ուսումնասիրությունը երաշխավորել որպես այդպիսի հավանական հիմք A-ի համար:
2°. Հետևանքի ուսումնասիրելը: Դիցուք պետք է ապացուցել, որ երկու մեծություններ իրար հավասար են: Նշանակենք S-ով r շառավիղ ունեցող գնդոլորտի մակերևույթի մակերեսը և ենթադրենք, օրինակ, որ պատրաստվում ենք ապացուցել թեորեմը, որ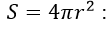

Հնարավոր է, որ սկզբում նպատակահարմար է փորձել ապացուցելը ավելի քիչը, հատկապես B թեորեմը, որը պնդում է, որ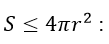

(Մենք, հավանաբար, կարող ենք ապացուցել B-ն՝ գնդոլորտը մոտարկելով ներգծյալ բազմանիստերով): Ինչ էլ որ լինի, ակնհայտ է, որ B-ն հետևում է A-ից, B թեորեմը A թեորեմի հետևանք է, այսինք՝ B-ն ավելի թույլ է, քան A-ն:
Սակայն ավելի թույլ B թեորեմի ապացույցը, ի վերջո, կարող է մեզ հասցնել սկզբնական A թեորեմի ապացույցին: Իսկապես, B-ն ապացուցելու համար օգտագործված դատողությունները կարող են հուշել ուրիշ՝ ավելի թույլ թեորեմի ապացույցի ձև, որը արտահայտվում է հակառակ իմաստով անհավասարությունով (հնարավոր է, այստեղ օգտակար է անցում կատարել ներգծված բազմանկյուններից արտագծվածների): Իսկ նշված երկու ավելի թույլ թեորեմների համադրությունից կստացվի սկզբնական A թեորեմը: Նման իրավիճակներ մաթեմատիկական հետազոտություններում բավականին հաճախ են հանդիպում:
Ի վիճակի չլինելով ապացուցել ելման A թեորեմը, հորինում ենք B թեորեմը որպես ցատկահարթակ և, օգտագործելով B թեորեմի ապացուցման պրոցեսում ստացած խթանը, հասնում ենք A-ի ապացույցին: Սա կարող է հանդիպել նույնիսկ ամենապարզ թեորեմներ ապացուցելիս: Այսպես, օրինակ, կարելի է ապացուցել ընդհանուր դեպքին վերաբերող A թեորեմը, սկզբում ապացուցելով մասնավոր դեպքին վերաբերող ավելի թույլ B թեորեմը, իսկ հետո B-ն օգտագործել որպես ցատկահարթակ:
Չե՞ք կարող դուք էլ ինչ-որ օրինակ բերել:

6. Դիցուք m-ը և n-ը դրական թվեր են, ընդ որում m>n:
   Համեմատեք հետևյալ խնդիրները.
   Ա. Գտեք m և n թվերի ընդհանուր բաժանարարները:
   Բ. Գտեք m և m-n թվերի ընդհանուր բաժանարարները։
   Ի՞նչ տրամաբանական կապ կա Ա և Բ խնդիրների միջև:
   Եթե պահանջվում է լուծել Ա խնդիրը, չե՞ք նկատում՝ որոշակի առավելություն ունի Ա խնդրից Բ-ին անցնելը:
   Օգտագործեք այդ ակնարկը 437-ի և 323-ի ընդհանուր բաժանարարները գտնելու համար:
    
7. Համեմատեք հետևյալ խնդիրները.
   Ա. Գտեք f(x) ֆունկցիայի մեծագույն արժեքը:
   Բ. Գտեք x-ի արժեքը, որի համար f(x) ֆունկցիայի f՛(x) ածանցյալը զրո է դառնում:
   Ի՞նչ տրամաբանական կապ կա Ա և Բ խնդիրների միջև:
   Տեսնո՞ւմ եք՝ որոշակի առավելություն ունի Ա խնդրից Բ-ին անցնելը:
    
8. Վերցնենք կամյական եռանկյուն և նշանակենք. 
   նրան արտագծած շրջանագծի կենտրոնը՝ O,
   միջնագծերի հատման կետը (ծանրության կենտրոնը)՝ G,
   Օ և G կետերով անցնող ուղղի վրա E կետը այնպես, որ 2OG=GE (ենթադրվում է, որ G-ն O և E կետերի միջև է):
   Դիտարկենք հետևյալ երկու թեորեմները.
   Ա. Եռանկյան երեք բարձրությունները հատվում են մի կետում:
   Բ. Եռանկյան երեք բարձրություններն անցնում են E կետով:
   Ի՞նչ տրամաբանական կապ կա Ա և Բ խնդիրների միջև:
   Նկատո՞ւմ եք՝ որոշակի առավելություն ունի Ա խնդրից Բ-ին անցնելը:
   Լուծեք Բ խնդիրը:
    
9. Համեմատեք հետևյալ երկու խնդիրները (նկատի է ունենում արմատների թվաբանական արժեքները):
   Ա. Ապացուցեք, որ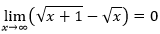
   
   Բ. Տրված  դրական թվի համար գտեք x-ի դրական արժեք, որոնց համար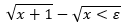
   
   Ի՞նչ տրամաբանական կապ կա Ա և Բ խնդիրների միջև:
   Լուծեք Բ խնդիրը:
    
10. Համեմատեք հետևյալ երկու խնդիրները (n-ը դրական ամբողջ թիվ է).
    Ա. Ապացուցեք (կամ ժխտեք) պնդումը՝ Եթե 2ⁿ-1-ը պարզ թիվ է, n-ը նույնպես պարզ թիվ է:
    Բ. Ապացուցեք (կամ ժխտեք) պնդումը՝ Եթե n-ը բաղադրյալ թիվ է, 2ⁿ-1-ն էլ կլինի բաղադրյալ:
    Ի՞նչ տրամաբանական կապ կա Ա և Բ պնդումների միջև:
    Չե՞ք գտնում եք Ա-ից Բ անցնելու որոշ առավելություն:
    Ապացուցեք Բ պնդումը:
     
11. Հակասող օրինակ փնտրելը: Հակասող օրինակը խախտում է այն պնդումը, որը իր բովանդակությամբ պետք է որ ճիշտ լիներ որոշ տեսակի բոլոր օբյեկտների համար. հակասող օրինակը այդ տեսակից նշում է օբյեկտ, որի համար ճիշտ չէ այդ, իբրև ընդհանուր, պնդումը: Հակասող օրինակ փնտրելն ունի որոշակի հետաքրքիր առանձնահատկություններ, որոնց քննարկումն օգտակար է, չնայած եթե ցանկանում ենք ցուցադրությունը բավականաչափ ուսուցողական դարձնել, ստիպված կլինենք մի քիչ շեղվել այս գրքում ընդունված շարադրանքից:

1°. Ապացուցման խնդիր: Ապացուցեք կամ հերքեք հետևյալ պնդումը.
Եթե իրական անդամներով a₁+a₂+a₃+… անվերջ շարքը զուգամիտում է, ապա 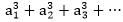անվերջ շարքը նույնպես կզուգամիտի:
Երկար բարակ շարունակական մտորումներից հետո կարող ենք կասկածել, որ առաջդրված պնդումը կեղծ է, և այդ ժամանակ կփորձենք այն հերքել հակասող օրինակի միջոցով:
2°. Ապացուցման խնդրի համար օժանդակ խնդիր գտնելու հարցը:
Մենք հակասող օրինակ ենք փնտրում, այլ խոսքերով՝ անվերջ շարք, որը կբավարարի պայմանին, բայց չի բավարարի 1° կետում պարունակվող եզրակացությանը: Այսպիսով, մեր առջև, ըստ էության, որոշման խնդիր է: Դիտարկենք նրա գլխավոր տարրերը:
Ի՞նչ է իրենից ներկայացնում անհայտը: Իրական թվերի a₁+a₂+a₃+... անվերջ հաջորդականություն:
Ո՞րն  է պայմանը: Այն երկու մաս ունի՝

1. a₁+a₂+a₃+... շարքը զուգամիտում է:
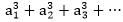2. շարքը տարամիտում է:
   Նկատենք, որ որոշման այս խնդիրն առաջացավ որպես ապացուցման խնդրի համար օժանդակ խնդիր:

3°. Պահանջվում է գտնել միայն մեկ (կամայական) օբյեկտ, որը կբավարարի պայմանին: Սովորական որոշման խնդիրներում սովորաբար խոսքը խնդրի պայմանին բավարարող բոլոր լուծումները, բոլոր օբյեկտները գտնելու մասին է: Մեր դեպքում բավական է գտնել մեկ լուծում, այդպիսի մեկ օբյեկտ. բավական է մեկ հակասող օրինակ, որպեսզի հերքվի կարծես ընդհանուր պնդումը:
Սովորականից տարբերվող այսպիսի իրավիճակը կարող է ուրիշ ռազմավարություն պահանջել: Այս հարցում Լեյբնիցը որոշակի խորհուրդ ունի. «Երբեմն կարող են պահանջվել բոլոր լուծումները, իսկ երբեմն՝ միայն մի քանիսը: Նման դեպքում, երբ պետք է միայն մեկ լուծում գտնել, պետք է սկզբնականի հետ համատեղելի  լրացուցիչ պայման մտածել, ինչի համար հաճախ մեծ վարպետություն է պահանջվում»:
4°. Պայմանը նեղացնելը: Մենք կսկսենք զուգամետ շարքերն ուսումնասիրելուց, որոնք բավարարում են խնդրի պայմանի առաջին մասին՝ հույս ունենալով դրանց մեջ գտնել այնպիսին, որը կբավարարի և երկրորդին: Բնական է փնտրելն սկսելը պարզագույն և լավ ծանոթ դեպքերից:
Սկզբում կարող ենք մտածել դրական a_n անդամներով զուգամետ շարքերի մասին: Բայց այդպիսի շարքերում a_n<1 մեծ n-երի համար, այդ պատճառով էլ 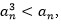, այնպես, որ  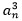ընդհանուր անդամով շարքը նույնպես կզուգամիտի: Այսպիսով, երկրորդ պայմանը չի կատարվի, և ստիպված ենք դիտարկել ոչ միայն դրական անդամներով շարքերը, այլև՝ բացասական անդամներով:
Այստեղ առավել հայտնի են նշանափոխ շարքերը, որոնցում անդամների նշանները կազմում են հետևյալ տեսքի շարք՝
+ - + - + - + - + - +….
Եթե այդպիսի շարքի a_n անդամները բացարձակ արժեքով նվազում են՝ ձգտելով զրոյի, շարքը զուգամիտում է, բայց այդ դեպքում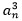թվերը նույն կերպ կդրսևորվեն, և դրանցով կազմված շարքն էլ կզուգամիտի: Նորից երկրորդ պայմանը չի կատարվում, և ստիպված ենք դիմել պակաս ծանոթ բնագավառներին:

Քանի որ ռիսկի գնալը ցանկալի չէ՝ չափազանց հեռանալով սովորաբար դիտարկվող դեպքերից, կարող ենք հանգել այդպիսի սահմանափակման մտքին:

3. a_n անդամների նշանները կազմում են այսպիսի շարք՝ +--+--+--+--...
   Նույնիսկ I և II պայմաններին III –ը ավելացնելիս էլի բավականին լայն դաշտ է մնում ազատ ընտրություն կատարելու համար: Այսպիսով, կարող է միտք առաջանալ էլի մեկ (ըստ էության ոչ այնքան ճշգրիտ ձևակերպված) սահմանափակում.
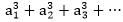    շարքը զուգամիտության հարցում պետք է հիշեցնի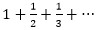հարմոնիկ շարքը։
4. Մեր սեփական նախաձեռնությամբ արված այս III և IV պահանջները էականորեն նեղացնում են պայմանները (տե՛ս դիտողություն 4-ի լրացումը): Նրանք կարող են մեզ հաջողությամբ ուղղորդել հակասող օրինակ փնտրելու գործում, բայց կարող են և արգելակել աշխատանքը: Ամեն դեպքում ինձ թվում է, որ նրանցից օգուտը ավելի շատ կլինի, քան խոչընդոտները, սակայն ընթերցողը պետք է ինքը փորձի հակասող օրինակ գտնել և այս մասին մշակի իր սեփական կարծիքը:

5°. Ապացույցների հերթագայության ընթացակարգը: Այստեղ հավանաբար հարմար առիթ է, որպեսզի հիշեցնենք ընթացակարգի մասին, որին պետք է ծանոթ լինի ապացուցման խնդիրներ լուծելու հմտություն ձեռք բերել ցանկացող մեկը:
Դիցուք՝ մեր առջև ապացուցման խնդիր է, որում կա հստակ ձևակերպված Ա պնդումը, ընդ որում հայտնի չէ՝ այն ճշմարիտ է, թե ոչ. մենք անորոշության և կասկածանքի վիճակում ենք: Խնդիրը լուծելով՝ նպատակ ենք դնում վերացնելու այդ կասկածը, այսինքն՝ ապացուցել կամ ժխտել:
Այսպես երբեմն հաջողվում է մոտեցում մշակել, որը երկու դեպքում էլ պիտանի կլինի, այսինքն՝ մոտեցում, որը մեզ կմոտեցնի Ա պնդումը ապացուցելուն կամ այն ժխտելուն՝ անկախ նրանից, թե իրականում որն է ճիշտ, այլ կերպ ասած՝ մոտեցում, որը ամեն դեպքում մեզ մոտեցնում է խնդրի լուծմանը: Սակայն նման հաջողությունները հազվադեպ են պատահում: Եվ եթե մեր բախտը չբերի լավ մոտեցում գտնելու հարցում, անհրաժեշտություն կլինի Ա պնդումը ապացուցելու կամ հերքելու վճիռ կայացնել: Մենք այս երկու ուղղությունների միջև ընտրություն պետք է կատարենք: Որպեսզի ապացուցենք Ա պնդումը, կա՛մ պետք է ուղղակի փնտրենք ինչ-որ պնդումներ, որոնցից այն հետևում է, կա՛մ դրա համար հատուկ ռազմավարություն մշակենք: Ա-ն հերքելու համար պետք է գտնել հակասող օրինակ:
Լավ սխեմա կլինի երկու ուղղություններով հերթագայությամբ դատողությունները: Երբ որևէ ուղղությամբ արդյունքի հասնելու հույսը մարում է, կամ այդ ուղղությամբ աշխատանքը մեզ հոգնեցնում է, դիմում ենք մյուս ուղղությանը՝ պատրաստ լինելով, եթե դա կպահանջեն հանգամանքները, նորից վերադառնալու սկզբնական ուղղությանը. այսպիսով, երկու ուղղություններով աշխատանքի ընթացքում տեղեկություններ հավաքելով, կարող ենք վերջապես հասնել հաջողության:

6°. Ապացույցների հաջորդագայության նշված ընթացակարգի ավելի բարդացված տարբերակը կա, որը կարող է պահանջվել ավելի դժվար դեպքերում և որի միջոցով կարելի է ավելի լուրջ արդյունքների հասնել:
Եթե ի վիճակի չենք ապացուցելու առաջադրված Ա պնդումը, փորձում ենք դրա փոխարեն ապացուցել ավելի թույլ պնդում (որը հաստատելը ավելի մեծ հնարավորություն ունի): Եթե չենք կարողանում ժխտել մեզ առաջադրված պնդումը, ձգտում ենք նրա փոխարեն ապացուցել ավելի ուժեղ պնդում (որի կեղծ լինելը բացահայտելը ավելի հեշտ է): Եթե մեզ հաջողվել է ապացուցել Բ պնդումը, փորձում ենք դրանից հետո ժխտել (պատշաճ կազմված) ավելի խիստ պնդումը, քան Բ-ն: Եթե մեզ հաջողվել է մերժել Բ պնդումը, փորձում ենք դրանից հետո ապացուցել (պատշաճ կազմված) ավելի թույլ պնդումը, քան Բ-ն: Երկու ուղղություններով առաջ գնալով դեպի Ա պնդման ապացույցը՝ ի վերջո կկարողանանք ապացուցել այն: Կամ կարող ենք ավելին անել, քան պարունակում է Ա պնդումը, այսինքն՝ կա՛մ ապացուցել Ա-ից ավելի խիստ պնդումը, կա՛մ ժխտել Ա-ն և դրա հետ միասին պարզել Ա պնդման որոշ մասի ճշմատացիությունը՝ այդպիսով ապացուցելով Ա-ից ավելի թույլ պնդում:
Առաջ գնալով ապացուցների և հակասող օրինակների կառուցման հաջորդագայության այս ճանապարհով՝ կարելի է հասնել ավելի ամբողջական գիտելիքի: Կարող ենք, օրինակ, պարզել, որ ինչ-որ թեորեմ ոչ միայն ճշմարիտ է (քանի որ արդեն ապացուցել ենք), այլև որ այն խստացնելը այնքան էլ հեշտ չէ (քանի որ արդեն ժխտել ենք ավելի խիստ թեորեմ): Այստեղ ընդհանրապես բախվում ենք գիտության մեջ ապացույցի դերին:

7°. Ապացույցների հերթագայության հետագա ձևափոխություններ, հետաքրքիր պատմական օրինակներ և փիլիսոփայական նրբերանգներ  կարելի գտնել մատենագիտությունում բերված Ի. Լակատոշի աշխատանքում:  

12. Հարմար է գտնված ցանկացած լուծում: Ապացուցեք, որ գոյություն ունի տարամիտող հաջորդականությունների զույգ՝ a₁+a₂+a₃+...+a_n+...., b₁+b₂+b₃+...+b_n+..., նվազող դրական անդամներով՝ a₁>a₂>a₃ …, b₁>b₂>b₃…, այնպիսի, որ min(a₁,b₁)+min(a₂,b₂)+...+min(a_n,b_n)+... շարքը զուգամետ է: (Սովորականի նման min(a,b) նշանակում է a և b թվերից փոքրը (ոչ մեծը)):(Այստեղ պահանջվում է գտնել ձևակերպված պայմանին բավարարող ոչ բոլոր շարքերի զույգերը, այլ միայն մի (ինչ-որ) զույգ: Այսպիսով, կարելի է օգտագործել Լեյբնիցի խորհուրդը, որը մեջ էր բերվել 11-րդ վարժությունում՝ նեղացրեք լուծումների փնտրման շրջանակը (ջանալով այդ ընթացքում նոր դժվարություններ չստեղծել)):
     
13. Մասնավորացնելը և ընդհանրացնելը օգտակար օժանդակ խնդիրների կարևոր աղբյուրներ են:
    Դիցուք, պահանջվում է հետազոտել դրական ամբողջ n թվի բաժանարարների թվի հարցը, որը կնշանակենք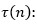  Այսպես, օրինակ (դիտարկում ենք մասնավոր դեպք, այսինքն՝ կիրառում ենք մասնավորեցում), 12 թիվն ունի վեց բաժանարար՝ 1, 2, 3, 4, 6 և 12 և այդ պատճառով  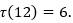այստեղ 12 թվի բաժանարարների մեջ ընդգրկված են 1 և 12 թվերը՝ «պարզագույն բաժանարարները», և հետագայում էլ այդպես կվարվենք բոլոր n-երի դեպքում:
    Մասնավորեցման ձևերից մեկն այն է, որ առանձին թվերը կոնկրետ դիտարկենք, օրինակ, կարելի է նկատել, որ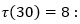 Կամ կարելի է համակարգված ձևով թվարկել 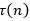-ի արժեքները՝ n=1, 2, 3...՝ կազմելով աղյուսակ, որի սկիզբը հետևյալ տեսքը ունի՝ 
    
    Մասնավորեցման ուրիշ ձև է, որ դիտարկենք թվերի որոշ դասեր: Եթե p-ն պարզ թիվ է, ապա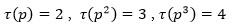
    
    Այստեղից, ընդհանրացնելով, եզրակացնում ենք, որ p պարզ թվի ցանկացած դրական ամբողջ աստիճանի համար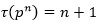
    
    Եթե p-ն և q-ն երկու տարբեր պարզ թվեր են, ապա pq արտադրյալն ունի ճիշտ չորս բաժանարար՝ 1, p, q և pq, և այդ պատճառով՝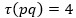
    
    Հետո կարող ենք դիտարկել երեք պարզ թվերի արտադրյալը և այլն: Ընդհանրացնելով, կարող ենք փորձել գտնել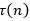 -ը, որտեղ n=p₁p₂…p_k k հատ տարբեր պարզ թվերի արտադրյալ է: Այս ճանապարհով գնալով, դիտարկելով երբեմն մասնավոր դեպքեր, իսկ հետո նորից ընդհանրացնելով կարելի է գտնել ընդհանուր արտահայտություն 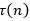-ի համար: (Գտեք այն):
    Այսպիսին է նոր փաստերը բացահայտելու ճանապարհները ոչ միայն թվերի տեսությունում, այլև մաթեմատիկայի մյուս բաժիններում և գիտության մեջ ընդհանրապես: Մասնավորեցնելով՝ ձգտում ենք առանձնացնել խնդրի առավել շոշափելի, առավել հասանելի մասը. դիմելով ընդհանրացումների՝ ձգտում ենք խստացնել այն արդյունքները, որոնք ձեռք ենք բերել սահմանափակ տիրույթում դիտարկումների արդյունքում: 
     
14. Նմանակումը նույնպես նոր փաստերի առատ աղբյուր է: Պարզագույն դեպքերում կարելի է գրեթե պատճենել մոտիկ, նման խնդիր: Ավելի բարդ դեպքերում փխրուն նմանակումը կարող է միանգամից իրական օգուտ չտալ, սակայն կարող է ցույց տալ ուղղությունը, որով պետք է շարունակել աշխատանքը:
    Դեպքերը, որտեղ կարող է կիրառվել նմանակումը, անհաշվելի են իրենց բազմազանությամբ. սա շատ օրինակներով ցուցադրվել է նախորդ (և հաջորդ) գլուխներում:
    Դրանցից միայն մեկ օրինակ բերեմ (գլուխ 1, § 6, կետ 3):  Պահանջվում է կառուցել սֆերիկ եռանկյան անկյունը, տրված երեք կողմերով: Այս կառուցումը կատարելու համար օգտագործվում է հարթաչափությունից մի նմանատիպ խնդիր՝ կառուցել սովորական եռանկյան անկյունը, իր տրված երեք կողմերով: Փորձեք նմանատիպ խնդիրների էլի մի քանի զույգեր հիշել:
    Ինչպես արդեն նշել ենք, նմանակումը օգտագործելու շատ ուրիշ ճանապարհներ կան:
     
15. Իսկ եթե չհաջողե՞նք: Հույսերը, որոնցով սկսում ենք ուսումնասիրել օժանդակ խնդիրը, կարող են չիրականանալ, մեր ձեռնարկումը կարող է ձախողվել: Բայց և այնպես ժամանակը և ջանքերը, որ ծախսել ենք օժանդակ խնդրի վրա, պետք չէ դատարկ կորուստ համարել. կարող ենք նաև անհաջողությունից ինչ-որ բան սովորել:
    Ցանկանում ենք ապացուցել Ա թեորեմը: Նկատում ենք ավելի խիստ Բ թեորեմը, որից հետևում է Ա թեորեմը: Մենք ձեռնամուխ ենք լինում Բ թեորեմը ապացուցելուն. եթե դա մեզ հաջողվի, դրանով կապացուցենք նաև Ա թեորեմը: Սակայն պարզվում է, որ Բ-ն կեղծ է: Դա ցավալի է, բայց փորձը, որը ձեռք կբերենք Բ թեորեմը ապացուցելիս, կարող է օգնել՝ ավելի լավ գնահատենք Ա թեորեմի ապացուցման հնարավորությունները:
    Մենք ցանկանում ենք ապացուցել Ա թեորեմը: Նկատում ենք Բ թեորեմը, որը Ա թեորեմի հետևանքն է, և որը կարող ենք ավելի հեշտ ապացուցել, քան Ա թեորեմը: Ձեռնամուխ ենք լինում Բ թեորեմի ապացուցմանը. եթե հաջողվի դա անել, կարող ենք Բ-ն օգտագործել որպես բանալի Ա թեորեմը ապացուցելու համար: Դիցուք, իսկապես կարողացանք ապացուցել Բ թեորեմը, բայց Բ-ն որպես Ա թեորեմի բանալի օգտագործելու մեր բոլոր փորձերը հաջողություն չունեցան: Սա ցավալի է, բայց Բ թեորեմը ապացուցելիս ձեռք բերված փորձը, կարող է մեզ օգնել ավելի լավ գնահատել Ա թեորեմն ապացուցելու հնարավորությունները:
     
16. Այլ խնդիրներ: Նկատելով, որ օժանդակ խնդիրները օգտակար եղան որոշակի խնդիրներ լուծելու համար, փորձեք պարզել, թե ինչու դա պատահեց, և որտեղից հայտնվեցին այս խնդիրները:
    Ինչո՞ւ: Բացատրեք սկզբնական և օժանդակ խնդիրների միջև կապը. տես 6-10 վարժությունները:
    Որտեղի՞ց: Օժանդակ խնդիր առաջանո՞ւմ է (կամ կա՞ առաջանալու հնարավորություն) հակառակ ուղղությամբ գնալու արդյունքում (վերջից սկիզբ շարժվելը), ընդհանրացնելով, մասնավորեցնելով կամ նմանակելով: Թե՞ դրա համար ուրիշ (ոչ այդքան հաճախ հանդիպող) աղբյուրներ են պահանջվում: