Պլան և ծրագիր

Մաթեմատիկական հայտնություն

7-րդ գլուխը

Գլուխ 8

Ցանկությունը միտք է ծնում որոշակի միջոցների մասին, որոնց օգնությամբ իրականացված ենք տեսնում մի բան, որը նման է մեր ձգտածին, այդ մտքից՝ այդ միջոցներին հասնելու միջոցների մասին միտք, և այդպես շարունակ, մինչև հասնենք որոշակի սկզբի, որը մեր սեփական իշխանության տակ է: 
Թոմաս Հոբս «Լևիաթան, կամ եկեղեցական և քաղաքացիական պետության նյութը, ձևաչափը և իշխանությունը»

§1. Պլան կազմելը որպես խնդիր լուծելու մեթոդ

Հոբսի խոսքում, որ բերված է այս գլխի նախաբանում, հիանալի հակիրճությամբ և ճշգրտությամբ շարադրված է հիմնավորապես կարևոր մեթոդ, ինչը որոշում է խնդիր լուծելու պրոցեսը: Ձգտենք ավելի խորը թափանցել հենց նոր մեջբերված տողերում և բազմակողմանի ընդգրկենք այդ պրոցեսը՝ դեպքերի ամբողջ բազմազանությամբ, որտեղ այն կարող է կիրառություն գտնել:

Եվ այսպես, խնդիր ունենք: Այլ կերպ ասած՝ ունենք Ա նպատակ, որին անմիջապես չենք կարող հասնել և ձգտում ենք հասնելու գործողության հարմար ձև գտնել: Այդ նպատակը կարող  լինել կիրառության կամ տեսության ոլորտում, հնարավոր է, որ վերաբերի մաթեմատիկային՝ գուցե լինի մաթեմատիկական որևէ օբյեկտ (թիվ, եռանկյուն,...), որ ցանկանում ենք գտնել (հաշվել, կառուցել…)։ Ինչպիսին էլ որ լինի Ա նպատակը, ցանկանում ենք դրան հասնել:

«Ցանկությունը միտք է ծնում որոշակի միջոցների մասին». սա մտքի՝ լավ նկատված հատկություն է: Նպատակը հուշում է միջոցը. սովորաբար ցանկությունից հետո որոշակի գործողությունների մասին միտք է ծնվում, որոնք անհրաժեշտ են այդ ցանկությունն իրականացնելու համար: Մտածում եմ ինչ-որ իրի մասին, որը կցանկանայի ունենալ, և անմիջապես հիշում եմ, թե որ խանութից կարող եմ գնել:

Վերադառնանք Հոբսի բառերին. «Ցանկությունից որոշակի միջոցների մասին միտք է ծնվում»՝ Բ, ինչի միջոցով կարելի է ստանալ Ա-ն: Հնարավոր է, որ այդ միտքը հիմնվում է նախօրոք ձեռք բերած փորձի վրա. «Արդեն մենք հնարավորություն ունեցել ենք նկատելու, որ Բ-ն ծնում է Ա-ի նման ինչ-որ բան, որին ձգտում ենք»: Ինչ էլ որ լինի, կարծում ենք, որ կհասնենք Ա-ին, եթե ունենանք Բ-ն: Իսկ Բ-ի մասին մտածելիս առաջանում է միջոցների մասին Գ միտքը, որի միջոցով կարելի է ստանալ B-ն՝ կարող ենք ստանալ Բ-ն, եթե ունենանք Գ-ն: «Եվ այդպես շարունակ՝ հաջորդաբար»՝ կկարողանանք ստանալ Գ-ն, եթե ունենանք Դ-ն, «մինչև հասնենք որոշակի սկզբի, որը մեր իշխանության տակ է». կարող ենք ստանալ Դ-ն, եթե ունենայինք Ե-ն, բայց Ե-ն ունենք: Այդ Ե-ի վրա ավարտվում է մեր մտքի ընթացքը՝ Ե-ն ունենք, այն «մեր իշխանության ներքո է», տրված է, հայտնի է:

Մեր մտքերի շղթան շատ «եթե»-ներ է պարունակում, «սա, եթե մյուսը», «կարող ենք սա ստանալ, եթե ունենանք այն»: Իսկապես, ասում ենք.

Ա եթե Բ,    Բ եթե Գ,     Գ եթե Դ,    Դ եթե Ե

Ե-ի վրա կանգ ենք առնում, քանի որ Ե-ն կատարված է անվերապահորեն՝ առանց լրացուցիչ «եթե»-ների:
(Գրեթե ավելորդ է նշելը, որ «եթե»-ների քանակը, այսինքն՝ միջանկյալ քայլերի թիվը, այստեղ նշանակություն չունի. մեր դեպքում կա չորս քայլ և հինգ «նպատակ» կամ «օբյեկտ». ընդհանուր դեպքում կլինի n քայլ և n+1 օբյեկտ):

Ինչի մասին նոր խոսում էինք, կարելի է անվանել պլանի կազմում: Դրան, իհարկե, պետք է հետևի պլանի իրականացումը: Սկսելով Ե-ից, ինչը մեր իշխանության տակ եղած սկիզբն է, պետք է ստանանք Դ-ն, գտնելով Դ-ն՝ գնանք դեպի Գ-ն, Գ-ից՝ Բ-ն, և Բ-ից ցանկալի Ա նպատակին:

Նշենք, որ պլանի կազմելը և դրա իրականացումը հակառակ ուղղություններով են գնում: Պլանը կազմելն սկսում ենք Ա-ից (նպատակ, անհայտ, եզրակացություն) և ավարտում Ե-ին հասնելով (տրված օբյեկտներ, տվյալներ, պայմաններ): Իսկ պլանն իրականացնելու ընթացքում, հակառակը, շարժվում ենք Ե-ից դեպի Ա-ն. այսպիսով, Ա-ի, այսինքն՝ մեր նպատակի մասին սկսում ենք մտածել ամենասկզբում, իսկ դրան հասնում ենք ամենավերջում: Եթե դեպի նպատակը շարժվելու ուղղությունը համարենք շարժում ճիշտ ուղղությամբ, կարելի է ասել, որ պլանը կազմելիս շարժվել ենք հակառակ ուղղությամբ: Այսպիսով, Հոբսի նկարագրած՝ խնդիր լուծելու կարևոր մեթոդը կարելի է անվանել հակառակ ուղղությամբ պլան կազմել կամ վերջից դեպի սկիզբը շարժվել. հույն երկրաչափները այս մեթոդն անվանում էին վերլուծություն, ինչը ըստ էության նշանակում է «լուծել վերջից դեպի սկիզբ»: Եթե գնում ենք հակառակ ուղղությամբ, այսինքն՝ մեր ունեցած օբյեկտներից դեպի նպատակ (մեր դեպքում Ե-ից դեպի Ա-ն), լուծման այդպիսի մեթոդը, ի հակադրություն առաջին մեթոդի, անվանում են շիտակ ուղղությամբ պլանի կազմում, կամ սկիզբից վերջ շարժում, կամ համադրում (ինչը հուներեն նշանակում է միավորում):

Ընթերցողին խորհուրդ է տրվում որևէ պարզ օրինակի վրա իր համար տեսանելի պատկերացնել պլանը կազմելու աշխատանքը՝ սկզբից դեպի վերջ, և վերջից դեպի սկիզբ աշխատանքը՝ այն իրակացնելիս: «Կարող եմ ինձ հետաքրքրող Ա իրը գնել այսինչ խանութից, եթե վճարեմ որոշակի Բ գումար. կարող եմ այդ Բ գումարը ճարել, եթե…»։ Հույս ունեմ, որ ընթերցողը հեշտությամբ կյուրացնի պլանը կազմելու տեխնիկան, և հույս ունեմ, որ նա երբեք չի դժվարանա այն իրականացնելիս:  

§2. Ավելի ընդհանուր մեթոդ

Փորձենք նախորդ պարագրաֆում շարադրված մեթոդի տեսանկյունից դիտարկել օրինակը, որը մանրամասն վերլուծել ենք գլուխ 7-ում (և այնտեղ էլ ցուցադրել ենք նկար 30-ով): Այդ օրինակից ելնելով՝ կարելի է անկասկածելիորեն պարզել մեթոդի ընդհանուր միտումը՝ պլանը կազմելու ընթացքում շարժվել հակառակ ուղղությամբ՝ անհայտից դեպի տվյալները և պլանը իրականացնելիս՝ ճիշտ ուղղությամբ, այսինքն՝ տվյալներից դեպի անհայտը: Ինչ վերաբերում է լուծման մանրամասներին, մեթոդը դրանք չի շոշափում:

Նայենք առաջին քայլը: §1-ում նկարագրելով պլան կազմելը՝ որպես խնդիրը լուծելու մեթոդ, ասում էինք, որ Ա-ն հանգում է Բ-ին, սկզբնական նպատակը փոխարինվում է երկրորդականով, Ա-ն գտնելը կախված է նրանից, թե Բ-ն հասանելի՞ է: Նկար 30-ում ցուցադրված օրինակում անհայտը հաշվելը (հատած բուրգի ծավալը) հանգում է երկու նոր անհայտները գտնելուն (երկու ծավալների). առկա է, ոչ թե երկրորդական մեկ նպատակ, այլ՝ երկուսը:

Սակայն, եթե մի անգամ էլ վերադառնանաք նկար 30-ում ցուցադրված պատկերին և հիշենք գլուխ 7-ում արված դիտողությունը՝ դրա գրաֆիկական ներկայացման մասին (մասնավորապես տես գլուխ 7-ի 5-րդ վարժությունը), դժվար չի լինի հասկանալը, թե ինչպես պետք է ընդհանրացնել §1-ում շարադրված մեթոդը, որպեսզի այն ընդգրկի ոչ միայն 7-րդ գլխում բերված օրինակը, այլև ուշադրության արժանի մեծ բազմությամբ օրինակներ:

Ո ւնենք Ա նկատակը: Անմիջապես չենք կարող դրան հասնել, բայց նկատում ենք, որ կկարողանայինք, եթե ունենայինք Բ՛, Բ՛՛, Բ՛՛՛ օբյեկտները: Ճիշտ է, դրանք դեռ չունենք, բայց արդեն սկսել ենք մտորել, թե ինչպես կարող ենք դրանք ստանալ, ուրիշ խոսքով՝ Բ՛, Բ՛՛, Բ՛՛՛ դիտարկում ենք որպես երկրորդական նպատակներ: Ավելի ուշ, որոշակի մտորումներից հետո պարզում ենք, որ մեր բոլոր երկրորդական նպատակները հասանելի են մի քանի նոր՝ Գ՛, Գ՛՛, Գ՛՛ օբյեկտներ ունենալու պայմանով: Իրականում այդ օբյկտները (Գ՛, Գ՛՛, Գ՛՛) նույնպես չունենք, բայց կարելի փորձել դրանք ստանալ. սա մեր երրորդ կարգի նպատակներն է և այլն: Այսպես հյուսում ենք մեր պլանի սարդոստայնը: Հնարավոր է, որ ստիպված լինենք հաճախ ասել. «Կարող ենք սա ունենալ, եթե ունենանք այն, և մյուսը, և երրոդը»,- և այսպես, մինչև կհասնենք ամուր հողի, այսինքն՝ օբյեկտների, որոնք իրականում ունենք մեր տրամադրության տակ: Մեր պլանի սարդոստայնը բաղկացած է մեր սկզբնական Ա նպատակին ենթակա օժանդակ նպատակներից և այդ նպատակների միջև կապերից: Այդպիսի ենթակա նպատակներ կարող են շատ լինել, և այդ պատճառով էլ մեր բարդ ցանցի, մեր սարդոստայնի կառուցման մանրամասները դժվար է բառերով նկարագրելը, բայց այդպիսի դեպքում օգնության է գալիս կետերից և գծերից կազմված դիագրամը, նման նրան, որը կառուցել ենք գլուխ 7-ում, օրինակ՝ 2-րդ գլխի §5–ի 3-րդ կետում մեր սկզբնական նպատակը S-ն էր, երկրորդականը՝ a, b, c և երրորդ կարգի նպատակները՝ l. m. n:

Ինձ թվում է, որ հենց նոր ասվածում պարունակվում է ավելի ընդհանուր մեթոդի բավականաչափ պարզ բնութագրում, որի մասնավոր դեպքը §1-ում նկարագրված մեթոդն է. այն կանվանենք վերջից դեպի սկիզբ շարժվելու մեթոդ: Այս մեթոդը պլան կազմելն է. երբ ելման կետը նպատակն է (փնտրվող օբյեկտ, անհայտ, եզրակացություն), և մենք շարժվում ենք վերջից դեպի սկիզբ՝ դեպի այն օբյեկտները, որոնք «մեր սեփական իշխանության» տակ են (հայտնի օբյեկտներ, տվյալներ, պայմաններ): Մեր պլանը ենթադրում է, որ նշված օբյեկտներին հասնելով, որոնց «տիրապետում ենք», դրանք կօգտագործվեն որպես «ելման օբյեկտներ», և, վերադառնալով սեփական հետքերով՝ ուղիղ ճանապարհով, կշարժվենք դեպի նպատակը (տես գլուխ 9, վարժություն 2-ի կետ 3):       

§3. Ծրագիր

Հավասա՞ր են արդյոք  և  թվերը: Եթե ոչ, նրանցից ո՞րն է մեծ: (Ենթադրվում է, որ բոլոր արմատները հասկացվում են թվաբանական իմաստով):

Հանրահաշվական ձևափոխություններ կատարելու ոչ մեծ փորձ ունենալով՝ դժվար չէ այդ հարցի պատասխանը ստանալու պլանը նշելը. նույնիսկ կարող ենք այնքան որոշակի ձևակերպել, որ այդպիսի պլանը բնութագրելու համար պահանջվում է հատուկ տերմին՝ ծրագիր:

Մեզ առաջադրված երկու թվերը կա՛մ հավասար են իրար, կա՛մ մեծ է առաջինը, կա՛մ մեծ է երկրորդը: Մեր երկու թվերի միջև հնարավոր է երեք հարաբերակցություն, որ արտահայտվում է =, > և < նշաններով, բայց դրանցից միայն մեկն է ճիշտ, հատկապես որը, դեռ չգիտենք, չնայած ցանկանում ենք իմանալ: Այդ միակ ճիշտ հարաբերակցության փոխարեն դնենք «?» նշանը և գրենք.

Այդ հնարավոր հարաբերություններից որն էլ ճիշտ լինի իրականում, կարող ենք որոշակի հանրահաշվական ձևափոխություններ կատարել, որոնք օրինական են բոլոր երեք դեպքերում էլ: Սկզբում, օրինակ, կարող ենք երկու մասերն էլ քառակուսի բարձրացնել. այդ դեպքում հարաբերությունը աջ և ձախ մասերի միջև չի փոխվի՝

Այս գործողության շնորհիվ քառակուսի արմատների քանակը նվազեցրեցինք՝ սկզբում չորսն էին, հիմա մնացին միայն երկուսը: Հետագայում աստիճանաբար կազատվենք նաև մնացած արմատներից և այդ ժամանակ կարող են պարզել, թե հնարավոր երեք հարաբերություններից որն է համապատասխանում «?» նշանին:

Անհրաժեշտ չէ, որ ընթերցողը կանխատեսի հետագա բոլոր հանրահաշվական ձևափոխությունները՝ բոլոր հետևանքներով, սակայն նրա համար պետք է պարզ լինի, որ դրանք կարող են կատարվել առանց դժվարության և անպայման կհանգեն ցանկալի արդյունքին: Նա նաև կարող է որոշել, որ տվյալ կոնկրետ դեպքում տեղին է հատուկ տերմին օգտագործելը, և որ նման մանրամասն կազմված պլանը պետք է ծրագիր կոչվի:

Վերջին դիտարկումը, ըստ էության, մեզ հասցնում է նպատակին, որը մեր առջև դրել էինք պարագրաֆի սկզբում, և ծրագրված քայլերի անհրաժեշտություն չկա: Ամեն դեպքում, եկեք դրանք կատարենք.

Հիմա հարցը լուծված է՝ իմացանք, թե թվերից որն է մեծ, և մեր հետքերով վերադառնալով, պարզում ենք, որ

§4. Ընտրություն մի քանի պլանից

Տրված եռանկյան (կամայական) կողմերի վրա, եռանկյունուց դուրս, կառուցեք երեք հավասարակողմ եռանկյուն և միացրեք նրանց կենտրոնները: Ապացուցեք, որ ստացված եռանկյունը հավասարակողմ է:

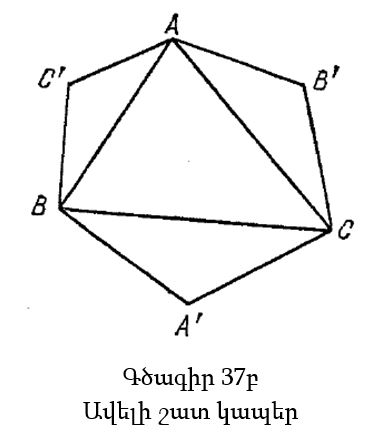
37ա նկարի վրա պատկերված է տրված ABC եռանկյունը. A՛, B՛, C՛ -ով նշանակված են համապատասխանաբար BC, CA, AB կողմերի վրա կառուցված եռանկյունների կենտրոնները: Պետք է ապացուցենք, որ A՛B՛C՛ եռանկյունը հավասարակողմ է, չնայած դա զարմանալի է թվում, գրեթե անհավանական. նախօրոք դժվար էր սպասելը, որ այդպիսի A՛B՛C՛ եռանկյան կողմերը հավասար կլինեն, որ նրա ձևը՝որը նկարագրված բավականաչափ բարդ կառուցումների արդյունք է, ամենևին կախված չէ սկզբնական (կամայական) եռանկյան տեսքից: Կարելի է ենթադրել, որ այդ ապացուցելը հեշտ չի լինի:

Նախ՝ մեզ դուր չեն գալիս А՛, В՛ և С՛  կետերը՝ նրանք 37ա նկարի մնացած մասից մեկուսացված են թվում: Բայց, այս թերությունն այնքան էլ լուրջ չէ: Դժվար չէ նկատելը, որ ВА՛С եռանկյունը հավասարասրուն է՝ A՛B=A՛C և BA՛C=1200: Մեր նկարի վրա կառուցելով այս եռանկյունը և նրա նմանակ մյուս երկու եռանկյունները, ավելի «կապակցված պատկեր» ենք ստանում:

Բայց դեռ չգիտենք, թե ինչպես մոտենանք նպատակին: Ինչպե՞ս կարելի է ապացուցել պահանջվող պնդումը: Էվկլիդեսի ոճո՞վ: Վերլուծական երկրաչափության միջոցո՞վ: Եռանկյունաչափություն կիրառելո՞վ:

1°. Ինչպե՞ս կարելի է, հետևելով Էվկլիդեսի ոճին, ապացուցել, որ A՛B՛=A՛C՛:

Դա կարելի է անել՝ ցույց տալով, որ A՛B՛-ը և A՛C՛-ը երկու հավասար եռանկյունների համապատասխան կողմեր են: Բայց մեր գծագրի վրա այդպիսի եռանկյուններ չկան, և դեռ չի երևում, թե ինչպես կարելի է ստանալ: Սա մեզ հուսաթափ է անում. փնտրենք՝ չկա՞ ուրիշ մոտեցում:

2°. Ինչպե՞ս վերլուծական երկրաչափության օգնությամբ ապացուցենք, որ A՛B՛=A՛C՛: Դիտարկենք A, B և C կետերի կոորդինատները՝ որպես տվյալներ, իսկ A՛, B՛ և C՛ կետերինը՝ որպես անհայտներ: Արտահայտելով անհայտ մեծությունները տվյալներով՝ կարող ենք այդ նոր տվյալներով գտնել մեզ հետաքրքրող հեռավորությունները, և, այսպիսով, պարզենք՝ նրանք իրար հավասար են, թե ոչ: Սա շատ հստակ ծրագիր է, բայց իրականացման համար պետք է գործ ունենանք վեց անհայտ մեծությունների և վեց տվյալների հետ. չէ, այստեղ էլ դուրեկան քիչ բան կա, երրորդ մոտեցումը փորձենք:

3°. Ինչպե՞ս կարող ենք եռանկյունաչափության միջոցով ապացուցել, որ A՛B՛=A՛C՛:

Համարենք ABC եռանկյան a, b և c կողմերը որպես տրված մեծություններ, իսկ B՛C՛=x, C՛A՛=y, A՛B՛=z որպես անհայտներ: Հաշվելով այդ անհայտ մեծությունները՝ կպարզենք՝ իսկապես z=y=z: Կարծես, այսպես շարժվելը իսկապես ավելի հեշտ կլինի, քան 2^o կետում. այստեղ ունենք երեք տվյալ և երեք անհայտ:

4°. Իրականում հարկ չկա բոլոր երեք անհայտները գտնել, բավական կլինի և երկուսը: Եթե y=z, A՛B՛C՛ եռանկյան ցանկացած երկու կողմերը կլինեն իրար հավասար, և սա արդեն բավական է:

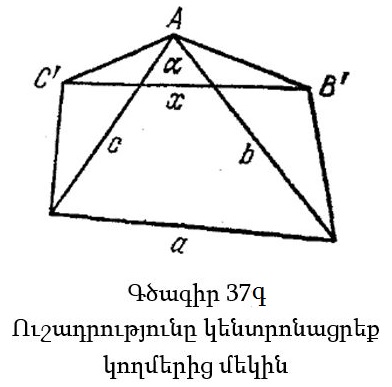
5°. Բացի դրանից, իրականում հարկ չկա նույնիսկ երկու անհայտը գտնել, եթե ավելի նուրբ դատողություններ կիրառենք, կարելի է և մեկով բավարարվել: Բավական է, օրինակ, արտահայտենք x-ը a, b և c-ի միջոցով, եթե հաջողվի ստանալ արտահայտություն, որը համաչափ է a, b, c-ի նկատմամբ, մեր նպատակին հասած կլինենք: (Արտահայտությունը կոչվում է համաչափ a, b, c-ի նկատմամբ, եթե տառերի տեղերը փոխելիս մնում է անփոփոխ): Իսկապես, եթե x-ի համար այդպիսի արտահայտություն ստանանք, այն ճիշտ կլինի նաև y-ի և z-ի համար: Չնայած այս ծրագիրը կախված է խնդիրը լուծողի հնարամտությունից, այսինքն փոքրիկ գաղափարի հայտնվելուց, այն բավականին գրավիչ է թվում. ընթերցողին օգտակար կլինի այս ծրագիրն իրականացնել փորձելը (տես գծագիր 37գ և վարժություն 3):

6°. Կարո՞ղ ենք մեր պատմությունից ուսուցանող ինչ-որ բան ստանալ: Ինձ թվում է՝ այո: Եթե մի քանի պլան ունեք, ընդ որում դրանցից ոչ մեկը հուսալի չէ, եթե ձեր գտնվելու դիրքից մի քանի ճանապարհ է գնում, դրանցից յուրաքանչյուրը ստուգեք ոչ մեծ երկարությամբ՝ նախքան դրանցից ինչ-որ մեկով հեռուն գնալը. կարող է ստացվել, որ հենց այդ ճանապրհը ձեզ փակուղի կտանի:

§5. Պլան և ծրագիր

Պլանը կարող ենք դիտարկել որպես ճանապարհ, որով պատրաստվում ենք ուղևորվել: Սակայն կարող են տարբեր պլաններ լինել: Ցանկալի է ունենալ այնպիսի պլան, որը ուղիղ կտաներ դեպի նպատակը, ցավոք սրտի, միշտ չէ, որ հնարավոր է լինում բավականաչափ լավ պլան կազմել, և, բացի դա, այնքան էլ շատ արդյունավետ գործողություններ պետք չեն նախնական պլան կազմելու համար: Երբեմն տեսնում ենք սպասվող ճանապարհի միայն փոքր հատվածը, երբեմն կարող է լինել մեծ հատված, իսկ լինում է, որ տեսանելի է լինում ամբողջ ճանապարհը՝ մինչև նպատակ: Հնարավոր է և, որ մեր ճանապարհը տեսնենք մշուշում կամ շատ պարզորոշ: Ճանապարհի այն մասում, որը վատ է երևում կամ ընդհանրապես չի երևում, մեզ կարող են տարբեր պատահականություններ հանդիպել, և մենք պետք է պատրաստ լինենք ցանկացած անակնկալների:

Այդ անակնկալներից ամենահաճելին (և դրա հույսը երբեք մեզ չպետք է լքի) կլինի պայծառ գաղափարի հայտնվելը, որը միանգամից կբացահայտի հարցի էությունը:

Շատ հաճախ վերջնական պլան չենք կարողանում գտնել, մեր պլանում լինում են խզումներ, չեն բավարարում որոշ կարևոր գաղափարներ: Բայց դա մեզ չի կանգնեցնում, ձեռնամուխ ենք լինում իրականացմանը՝ հույս ունենալով, որ կհայտնվի ինչ-որ պայծառ կամ ուղղակի նոր գաղափար, և որ դրա միջոցով կհաջողվի բացը լրացնել:

Լավ պլանը վատից տարբերվում է նրանով, որ պետքական գաղափար ծնվելու հույսը այստեղ ավելի մեծ է: Եթե մենք նոր գաղափարների կարիք չունենք, հակառակը, վստահ ենք, որ նախօրոք մտածված և նախատեսված քայլերը կապահովեն նպատակին հասնելը, մեր պլանը կարելի է համարել բավականաչափ հստակ և որոշակի, որպեսզի անվանենք (ամբողջական) գործողությունների ծրագիր: Երբեմն ստիպված ենք լինում բավականին շատ ժամանակ ծախսել տարբեր անկատար պլաններ մշակելու համար, նախքան դրանցից որևէ մեկը հաջողվում է դարձնել ծրագիր:

Համադրեք, օրինակ՝ 3-րդ, 4-րդ պարագրաֆների հետ:  

§6. Մեթոդ և պլան

Համապատասխան պայմանների դեպքում նախկինում մեր ուսումնասիրած մեթոդներից յուրաքանչյուրը ծնում է պլան, սակայն այդ մեթոդը միանգամից չի դառնում մանրամասն պլան, այսինքն՝ ծրագիր: Օրինակ, դիտարկենք երկրաչափական կառուցումների վերաբերյալ խնդիրները: Կարելի է փորձել լուծել երկու երկրաչափական տեղերի մեթոդով: Իհարկե, սա արդեն պլան է, սակայն լրացուցիչ գաղափարի կարիք ունի, որպեսզի գտնենք այն կետը, որի կառուցմանը կարելի է բերել խնդիրը, և որպեսզի խնդրի պայմանը երկու մասի բաժանենք, որոնք կծնեն այդ կետի դիրքը որոշող երկրաչափական տեղերը:

Կամ, ենթադրենք, ցանկանում ենք խնդիրը լուծել Դեկարտի մեթոդով՝ երբ խնդրի լուծումը հանգում է հավասարումների համակարգի: Իհարկե, սա էլ է պլան, սակայն այն պահանջում է լրացուցիչ գաղափարներ, որպեսզի կազմենք այնքան հավասարում, որքան անհայտ ունենք, ինչպես նաև էլի գաղափարներ, որպեսզի կարողանանք լուծել հավասարումների ստացված համակարգը:

Վերջից դեպի սկիզբը շատ ընդհանուր և օգտակար մեթոդ է պլան կազմելու համար, սակայն որպեսզի վերացնենք տվյալների և անհայտների միջև եղած խզումը, մեզ պետք կլինեն հարցի էությունից բխող գաղափարներ։ Երբ ետընթաց ուղղությամբ պլանը արդեն կազմված է, և խզումները պահող թելերի տրամաբանական միահյուսումը՝ ավարտված, պատկերը ամբողջովին փոխվում է: Այս դեպքում ունենք ծրագիր՝ սկզբից դեպի վերջը, տվյալներից դեպի անհայտները շարժվելու համար:

Վարժություններ և լրացուցիչ դիտարկումներ 8-րդ գլխի վերաբերյալ 

Թարգմանություն ռուսերենից 
Լուսանկարը՝ Գևորգ Հակոբյանի ՖԲ էջից