Մաթեմատիկոսի արդարացում

Սկիզբը

11

Շախմատային խնդիրը իսկական մաթեմատիկա է, բայց ինչ-որ իմաստով դա «պարզագույն» մաթեմատիկա է: Որքան էլ քայլերը նուրբ, յուրօրինակ և զարմանալի լինեն, ինչ-որ էական բան այնուամենայնիվ պակասում է: Շախմատային խնդիրները կարևոր չեն: Իսկական մաթեմատիկան լուրջ է ու գեղեցիկ, եթե կուզեք՝ «կարևոր», բայց այս բառը բազմիմաստ է, և «լուրջ» բառը ավելի լավ է արտահայտում այն, ինչ ցանկանում եմ ասել: 

Նկատի չունեմ մաթեմատիկայի «գործնական» հետևանքները: Այս հարցին դեռ կանդրադառնամ հետագայում, իսկ հիմա միայն ասեմ՝ եթե շախմատային խնդիրը, կոպիտ ասած, «անօգուտ» է, լավագույն մաթեմատիկայի մասին էլ հիմնականում կարելի է նույնը ասել, և մաթեմատիկայի միայն չնչին մասն է օգտակար, և մաթեմատիկայի այդ չնչին մասն էլ համեմատաբար անհետաքրքիր է: Մաթեմատիկական թեորեմի «լրջությունը» նրա կիրառական հետևանքը չէ (սովորաբար դա աննշան է), այլ մաթեմատիկական այն գաղափարների նշանակալիությունը, որոնց միջև թեորեմը կապ է հաստատում: Առանց մանրուքների մեջ մտնելու, կարելի է ասել, որ մաթեմատիկական գաղափարը «նշանակալի» է, եթե այն կարելի պարզ և բնական կերպով կապել մաթեմատիկական այլ գաղափարների լայն համակարգի հետ: Այսպիսով, լուրջ մաթեմատիկական թեորեմն այն թեորեմն է, որը կապում է «նշանակալի» գաղափարներ, ամենայն հավանականությամբ հանգեցնում է էական առաջխաղացումների բուն մաթեմատիկայի և նույնիսկ այլ գիտությունների մեջ: Գիտական մտքի զարգացման վրա շախմատային ոչ մի խնդիր ազդեցություն չի թողել. Պյութագորասը, Նյուտոնը, Էյնշտեյնը, յուրաքանչյուրը՝ իր ժամանակին, փոխել են գիտական մտքի ուղղությունը:

Հասկանալի է, որ թեորեմի լրջությունը նրա հետևանքներով չի որոշվում. հետևանքները միայն վկայում են նրա լրջության մասին: Շեքսպիրը հսկայական ազդեցություն է թողել անգլերենի զարգացման վրա, Օթուեյը[1]՝ համարյա բոլորովին, բայց Շեքսպիրը ավելի լավ բանաստեղծ էր ուրիշ պատճառով: Նա լավագույն բանաստեղծն էր, որովհետև նրա պոեզիան էր շատ ավելի լավը: Շախմատային խնդրի անկարևորությունը, Օթուեյի պոեզիայի նման, ոչ թե նրա հետևանքներից է, այլ բովանդակությունից:  

Մի հարց էլ կա, որին շատ կարճ կանդրադառնամ ոչ այն պատճառով, որ անհետաքրքիր է, այլ որովհետև բարդ է, և համապատասխան որակավորում չունեմ, որ գեղագիտական լուրջ քննարկում վարեմ: Մաթեմատիկական թեորեմի գեղեցկությունը մեծ մասամբ կախված է նրա լրջությունից. նույնիսկ պոզիայում տողի գեղեցկությունը ինչ-որ չափով կարող է կախված լինել ներդրված գաղափարներից: Վերևում շեքսպիրյան երկու տող էլ մեջբերել՝ որպես բառային նկարի իսկական օրինակ, բայց «Կյանքի տենդահույզ տագնապից հետո ննջում է անդորր» տողն ինձ ավելի գեղեցիկ է թվում: Պատկերը նույնքան գեղեցիկ է, բայց այս դեպքում գաղափարները իմաստալից են, պնդումը՝ առողջ, այդ իսկ պատճառով տողը մեր ավելի խոր զգացմունքներին է հասնում: Գաղափարները պատկերի վրա էական ազդեցություն են ունենում պոեզիայում էլ, և, բնական է, ավելի մեծ չափով՝ մաթեմատիկայում, բայց ես նույնիսկ չեմ փորձի այս հարցը ավելի լուրջ քննարկել:

12

Պարզ է դառնում, որ հետագա շարադրանքի համար պետք է «իսկական» մաթեմատիկական թեորեմների օրինակներ բերեմ. այնպիսի թեորեմների, որոնք ցանկացած մաթեմատիկոս առաջնակարգ կհամարի: Եվ այստեղ շատ դժվար դրության մեջ եմ հայտնվում այն սահմանափակումների պատճառով, որոնցում գրում եմ: Մի կողմից՝ իմ օրինակները շատ պարզ և մաթեմատիկական հատուկ գիտելիք չունեցող ընթերցողին հասկանալի պիտի է լինեն. չպետք է լինեն նախնական բարդ բացատրություններ, և ընթերցողը պետք է կարողանա հետևել ինչպես թեորեմի ապացույցին, այնպես էլ ձևակերպմանը: Այս պայմանները բացառում են, օրինակ, թվերի տեսության շատ գեղեցիկ թեորեմներ, ինչպես երկու քառակուսու մասին Ֆերմայի թեորեմը կամ քառակուսային կախվածության օրենքը: Մյուս կողմից՝ իմ օրինակները պետք է «առաջնակարգ» մաթեմատիկայից լինեն, ակտիվ աշխատող մասնագետ մաթեմատիկոսի մաթեմատիկայից, և այս պայմանը բացառում է շատ բան, ինչը կարելի էր հասանելի դարձնել ընթերցողների լայն շրջանակին, բայց ինչը դուրս է տրամաբանությունից և մաթեմատիկայի փիլիսոփայությունից:

Դժվար լինի սյս իրավիճակից դուրս գալու ավելի լավ ելք, քան հին հույների մաթեմատիկային դիմելը: Կձևակերպեմ և կապացուցեմ հինհունական մաթեմատիկայի երկու հայտնի թեորեմ: Այս երկու թեորեմն էլ պատկանում են «պարզերի» շարքին՝ ինչպես գաղափարով, այնպես էլ իրականացմամբ, բայց, անկասկած, նույնիսկ այս պարագայում երկուսն էլ բարձրագույն կարգի թեորեմներ են: Դրանցից յուրաքանչյուրը նույնքան թարմ և կարևոր է, ինչպես իր բացահայտման ժամանակ: Անցած երկու հազար տարին նրանց երեսին ոչ մի կնճիռ չի ավելացրել: Վերջապես, մտավորականը, որքան էլ աղքատ լինեն նրա մաթեմատիկական գիտելիքները, ընդամենը մեկ ժամվա ընթացքում կարող է հաղթահարել և´ ձևակերպումը, և´ ապացույցը:

1. Առաջին օրինակը Էվկիդեսի առաջարկած ապացույցն է, որ գոյություն ունեն անվերջ շատ պարզ թվեր:

Պարզ են կոչվում այն թվերը, որոնք հնարավոր չէ վերածել ավելի փոքր արտադրիչների` 2, 3, 5, 7, 11, 13, 17, 19, 29, ..., (1): Օրինակ, 37-ն ու 317-ը պարզ են: Հենց պարզ թվերն են այն նյութը, որից բազմապատկելու միջոցով կազմվում են բոլոր թվերը. օրինակ, 666 = 2•3•3•37: Ցանկացած թիվ, որը պարզ չէ, բաժանվում է գոնե մեկ պարզ թվի (հասկանալի է, որ կարող է բաժանվել է մի քանի պարզ թվերի): Պահաջվում է ապացուցել, որ անվերջ թվով պարզ թվեր կան, այսիքն` (1) հաջորդականությունը երբեք չի վերջանում:

Ենթադրենք, որ A) հաջորդականությունը վերջանում է, այսինքն` 2, 3, 5, . . ., P նրան պատկանող բոլոր թվերն են (այսպիսով, P-ն ամենամեծ պարզ թիվն է):  Հետևելով այդ վարկածին` դիտարկենք հետևյալ թիվը.

Q=2•3•5•...•P+1:

Պարզ է, որ Q թիվը չի բաժանվում 2, 3, 5, . . ., P թվերից ոչ մեկին, քանի որ դրանցից յուրաքանչյուրի վրա բաժանելիս կմնա 1 մնացորդ: Բայց, եթե Q թիվը պարզ չէ, պետք է որևէ պարզ թվի բաժանվի: Հետևաբար, գոյություն ունի այնպիսի պարզ թիվ (հնարավոր է հենց Q թիվը), որը ավելի մեծ  է, քան 2, 3, 5,... , Р թվերից յուրաքանչյուրը: Սա հակասում է մեր ենթադրությանը, թե գոյություն չունի P թվից ավելի մեծ պարզ թիվ. հետևաբար մեր ենթադրությունը սխալ է:

Ապացուցման reductio ad absurdum (հակասումով ապացույց) մեթոդը, որը շատ սիրում էր Էվկլիդեսը, մաթեմատիկոսների սիրած գործիքներից է:  Սա ավելի «խորամանկ» գամբիտ է, քան շախմատային ցանկացած գամբիտ. շախմատիստը կարող է զինվոր կամ նույնիսկ ֆիգուր զոհաբերել, իսկ մաթեմատիկոսը զոհաբերում է ամբողջ պարտիան:

13

2. Երկրորդ օրինակը Պյութագորասի առաջարկած ապացույցն է, որ 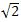 թիվը իռացիոնալ է:

Ռացիոնալ թվերը ներկայացվում են  a/b կոտորակի տեսքով, որտեղ a և b թվերը ամբողջ թվեր են: Կարելի է համարել, որ a և b թվերը ընդհանուր բաժանարար չունեն, քանի որ եթե ունենային, ապա կոտորակը կարելի էր կրճատել նրանց ընդհանուր բաժանարարով: «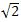 թիվը իռացիոնալ է» պնդումը համարժեք է «2 թիվը հնարավոր չէ ներկայացնել  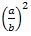տեսքով» պնդմանը, իսկ դա էլ իր հերթին համարժեք է այն պնդմանը, որ a²=2b² (2) հավասարմանը չեն կարող բավարարել ընդհանուր բաժանարար չունեցող a և b ամբողջ թվեր:

Զուտ թվաբանական այս թեորեմը չի պահանջում իմանալ «իռացոնալ թվերը» և կախված չէ իռացիոնալ թվերի ոչ մի տեսությունից:

Նորից օգտվենք հակասմամբ ապացուցելու եղանակից: Ենթադրենք, որ (2) առնչությունը տեղի ունի, և a-ն ու b-ն ընդհանուր բաժանարար չունեցող ամբողջ թվեր են: (2) առնչությունից հետևում է, որ a² թիվը զույգ է (քանի որ 2b²-ն բաժանվում է 2-ի), և հետևաբար, a թիվը զույգ է (քանի որ կենտ թվի քառակուսին կենտ թիվ է): Եթե a-ն զույգ է, ապա a=2c (3), որտեղ c-ն ամբողջ թիվ է, և, հետևաբար, 2b²=a²=(2c)²=4c², կամ b²=2c² (4):

Հետևաբար b² թիվը զույգ է, իսկ դա էլ նշանակում է (նույն պատճառով, ինչ առաջ), որ b թիվը զույգ է: Այսպիսով, a և b թվերը երկուսն էլ զույգ են, և այդ պատճառով էլ ունեն ընդհանուր բաժանարար՝ 2, ինչը հակասում է մեր սկզբնական ենթադրությանը: Հետևաբար, մեր սկզբնական ենթադրությունը սխալ է:

Պյութագորասի թեորեմից հետևում է, որ քառակուսու անկյունագիծը համաչափելի չէ իր կողմի հետ (որ նրանց հարաբերությունը ռացիոնալ թիվ չէ, որ գոյություն չունի երկարության այնպիսի միավոր, որի ամբողջ բազմապատիկները լինեն և´ անկյունագիծը, և´ կողմը):

Իսկապես, եթե կողմը ընտրենք որպես երկարության միավոր և անկյունագծի երկարությունը նշանակենք d, ապա Պյութագորասի էլի մի հայտնի թեորեմի համաձայն d²=1²+1²=2, այդ պատճառով էլ d-ն չի կարող ռացիոնալ թիվ լինել:

Կարող եմ թվերի տեսությունից էլի շատ գեղեցիկ թեորեմներ ներկայացնել, որոնց իմաստը հասկանալի լինի ցանկացած մարդու: Օրինակ, «թվաբանության հիմնական թեորեմ» անունով հայտնի պնդումն ասում է՝ ցանկացած ամբողջ թիվ կարող է վերլուծվել պարզ թվերի արտադրյալի, ընդ որում միակ (արտադրիչների հերթականության ճշտությամբ) ձևով: Օրինակ, 666=2•3•3•37, և ուրիշ վերլուծումներ գոյություն չունեն. 666=2•11•29, կամ 13•89=17•73 անհնար են (դրանում կարող ենք համոզվել առանց բազմապատկումները կատարելու): Այս թեորեմը, դա է վկայում նրա անվանումը, բարձրագույն թվաբանության հիմքն է, բայց նրա ապացույցը, չնայած «բարդ» չէ, պահանջում է որոշակի նախնական պարզաբանումներ և ոչ մաթեմատիկոս ընթերցողի համար կարող է ձանձրալի լինել:

Հայտնի և գեղեցիկ թեորեմի էլի մեկ օրինակ կարող է ծառայել Ֆերմայի թեորեմը երկու քառակուսիների մասին: Պարզ թվերը (եթե բացառենք 2 հատուկ պարզ թիվը) կարելի բաժանել երկու դասի՝

• պարզ թվեր` 5, 13, 17, 29, 37, 41 …, որոնք 4-ի բաժանելիս տալիս են մեկ մնացորդ,  
• և պարզ թվեր` 3, 7, 11, 19, 23, 31,... , որոնք 4-ի բաժանելիս տալիս են 3 մնացորդ:

Առաջին դասի բոլոր պարզ թվերը կարելի ներկայացնել երկու ամբողջ թվերի քառակուսիների գումարի տեսքով.

5 = 1²+2², 13 = 2²+3²,
17=1²+4², 29 = 2²+5²:

Երկրորդ դասի թվերից ոչ մեկը երկու ամբողջ թվերի քառակուսիների գումարի տեսքով հնարավոր չէ ներկայացնել (ընթերցողը կարող է հեշտությամբ համոզվել ստուգելու միջոցով): Այս պնդումը Ֆերմայի թեորեմն է, որը միանգամայն հիմնավոր կերպով ընդունված է թվերի տեսության գեղեցկագույն թեորեմներից մեկը համարել: Ցավոք, գոյություն չունի դրա` մաթեմատիկոս-մասնագետից բացի ուրիշ մեկին հասանելի ապացույց:

Գեղեցիկ թեորեմներ կան նաև բազմությունների տեսության մեջ, օրինակ, Կանտորի թեորեմը` կոնտինուումի ոչ հաշվելի լինելու մասին: Այստեղ դժվարությունը ճիշտ հակառակն է: Թեորեմի ապացույցը բավականին պարզ է, եթե տիրապետում եք բազմությունների տեսության տերմինալոգիային, բայց մինչև թեորեմի իմաստի հասկանալի դառնալը լայն պարզաբանումներ են անհրաժեշտ: Այդ պատճառով էլ նոր օրինակներ չեմ բերի: Վերը բերված օրինակները յուրօրինակ թեստեր են, և դրանք ըստ արժանավույն գնահատել չկարողացող ընթերցողը դժվար թե մաթեմատիկայում ընդհանրապես ինչ-որ բան կարողանա գնահատել:

Ինչպես արդեն ասվեց, մաթեմատիկոսը պատկերները կազմում է գաղափարներից, իսկ գեղեցկությունը և լրջությունը այն չափանիշներն են, որոնց միջոցով կարելի է դատել ստեղծված պատկերների մասին: Դժվարությամբ կհավատամ, թե ով բերված երկու թեորեմները հասկացել է, կարող է վիճել այն մասին, որ դրանք բավարարում են գեղեցկության և լրջության չափանիշներին: Եթե դրանք Դյուդենիի ամենասրամիտ գլուխկոտրուկների կամ իր բնագավառի վարպետի ստեղծած շախմատային լավագույն խնդիրների հետ համեմատենք, ապա թեորեմների` և՛ գեղեցկության, և՛ լրջության առումով գերազանցությունը պարզ կլինի. երևում է որակի ակնհայտ տարբերություն: Թեորեմներն ավելի լուրջ են, ինչպես նաև` շատ ավելի գեղեցիկ: Կարելի՞ է ավելի մանրամասն որոշել, թե որն է թեորեմների առավելությունը:

14

Ամենից առաջ մաթեմատիկական թեորեմների ակնհայտ և ճնշող առավելությունը լրջությունն է: Շախմատային խնդիրը հիմքում իրարից այնքան էլ չտարբերվող և արտաքին հետևանքներ չունեցող սրամիտ գաղափարների շատ սահմանափակ համախմբի արդյունք է: Մենք էլի նույն ձևով կմտածեինք, եթե անգամ շախմատը հայտնագործված չլիներ, մինչդեռ Էվկլիդեսի և Պյութագորասի թեորեմները խորը ազդեցություն են թողել մարդկային մտածողության վրա նույնիսկ մաթեմատիկայի սահմաններից դուրս:

Այսպիսով, Էվկլիդեսի թեորեմը կարևոր կենսական նշանակություն  ունի թվաբանության ողջ կառույցի համար: Պարզ թվերն այն հում նյութն են, որից պետք է կառուցենք ամբողջ թվաբանությունը, և Էվկլիդեսի թեորեմը մեզ համոզում է, որ այդ խնդիրը լուծելու համար բավարար քանակությամբ հում նյութ ունենք: Բայց Պյութագորասի թեորեմը կիրառման ավելի լայն դաշտ ունի և ավելի հաճելի ձևակերպում:

Պետք է նշել, որ Պյութագորասի առաջարկած ապացույցը հեռահար ընդհանրացումներ ունի և հիմնական սկզբունքի փոքր փոփոխությունից հետո կարող է կիրառվել «իռացիոնալ թվերի» շատ լայն դասի համար:

Պյութագորասի ապացույցի նմանությամբ կարող ենք ապացուցել (ինչպես, հավանաբար, դա արել է Թեետետոսը[2]), որ 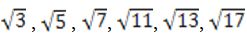 թվերն իռացիոնալ են, կամ (Թեետետոսի ապացույցի շրջանակից էլ դուրս) որ   թվերն իռացիոնալ են:

Էվկլիդեսի թեորեմն ասում է, որ ամբողջ թվերի ոչ հակասական թվաբանությունը կառուցելու համար մեր տրամադրության տակ բավարար քանակությամբ նյութի պաշար ունենք: Պյութագորասի թեորեմը և նրա ընդհանրացումները խոսում են այն մասին, որ երբ կառուցենք ամբողջ թվերի թվաբանությունը, այն մեր նպատակների համար բավարար չի լինի, քանի որ մեր ուշադրությունը գրավող շատ մեծություններ կան, որոնք ամբողջ թվերով չենք կարող չափել: Քառակուսու անկյունագիծը միայն ակնհայտ օրինակ է: Հին հույն մաթեմատիկոսներն այս հայտնագործության խորը իմաստն անմիջապես գիտակցեցին: Սկզբում նրանք համարում էին (իմ կարծիքով, ըստ «առողջ մտքի» «բնական» պահանջների), որ նույն սեռի բոլոր մեծությունները համաչափելի են, օրինակ, որ երկարության ցանկացած երկու մեծություն բազմապատիկ է երկարության նույն միավորին, և այս ենթադրությունից ելնելով` կառուցեցին հարաբերությունների տեսությունը: Պյութագորասի հայտնագործությունը ցույց տվեց, որ այդ ենթադրությունը ճիշտ չէր, և հանգեցրեց Եվդոքսի[3] ավելի խորը տեսությունը կառուցելուն` շարադրված Էվկլիդեսի «Սկզբունքներ» գրքի V հատորում: Եվդոքսի տեսությունը մեր ժամանակներում շատ մաթեմատիկոսներ հինհունական մաթեմատիկայի լավագույն ձեռքբերումներից են համարում: Այս տեսությունն իր ոգով զարմանալիորեն արդիական է և կարող է դիտարկվել որպես իռացիոնալ թվերի ժամանակակից տեսության ներածություն, ինչը հեղափոխություն արեց մաթեմատիկական անալիզում և ուժեղ ազդեցություն թողեց նորագույն ժամանակների փիլիսոփայության վրա:

Այսպիսով, թեորեմների «լրջության» վերաբերյալ ոչ մի կասկած չկա, ուստի ավելի լավ է նշենք, որ այդ թեորեմներից ոչ մեկը «գործնական» որևէ կիրառություն չունի: Գործնական կիրառության մեջ մեզ հետաքրքրում են միայն համեմատաբար փոքր թվերը: Միայն աստղագիտությունն ու ատոմային ֆիզիկան են աշխատում «մեծ» թվերի հետ, բայց այդ գիտություններն էլ, գոնե հիմա, հազիվ թե ավելի մեծ գործնական նշանակություն ունեն, քան մաքուր վերացարկված մաթեմատիկան: Չգիտեմ, թե ինչ ամենամեծ ճշգրտություն է անհրաժեշտ ճարտարագետին: Շռայլ լինենք և համարենք, որ խոսքը ստորակետից հետո տասը թվանշանի մասին է: Այդ դեպքում 3,14159265 թիվը ( թվի արժեքը ստորակետից հետո 8 նշի ճշտությամբ) կարելի է ներկայացնել 

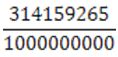
հարաբերության տեսքով, համապատասխանաբար, ինը նիշանոց, տասը նիշանոց: 

1000000000-ը չգերազանող պարզ թվերի քանակը 50847478 է: Սա բավական է ճարտարագետի համար, և նա կարող է երջանիկ զգալ առանց մնացածի: Էվկլիդեսի թեորեմի մասին ասվածը բավարար է: Ինչ վերաբերում է Պյութագորասի թեորեմին, ապա պարզ է, որ ճարտարագետի համար իռացիոնալ թվերն ընդհանրապես հետաքրքրություն չեն ներկայացնում, քանի որ միշտ գործ ունի մեծությունների մոտավոր արժեքների հետ, իսկ բոլոր մոտավոր արժեքները ռացիոնալ են:

Շարունակությունը

Թարգմանություն ռուսերենից

Լուսանկարը` «Բրիտանիկա» հանագիտարանի կայքից