Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Սկիզբը 
Նախորդ հատվածը

Գլուխ 9
Թվային առանցքից դեպի թվային հարթություն

Ներմուծենք «i» թիվը

Մինչև այժմ քառակուսի արմատները քննարկելիս զգուշորեն խուսափում էի բացասական թվերը հիշատակելուց: Օրինակ, ասում էի, որ 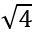=2, քանի որ 2x2=4: Սակայն ճիշտ է նաև 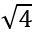=-2 արտահայտությունը, քանի որ (-2)х(-2)=4: (Հուսով եմ, չեք մոռացել, որ երկու բացասական թվերի արտադրյալը դրական թիվ է):

Հետևաբար, 4 թիվը երկու քառակուսի արմատ ունի և կարելի է գրել հետևյալ տեսքով` 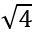=±2: «±» սիմվոլը նշանակում է «կա՛մ պլյուս, կա՛մ մինուս»:

Սակայն, եթե +2 և -2 թվերը երկուսն էլ 4-ի քառակուսի արմատն են, ո՞ր թիվ կլինի -4-ի քառակուսի արմատը: Իհարկե,  +2х(-2)=-4, սակայն +2-ը և -2-ը նույնը չեն: Այնպես որ այս երկու տարբեր թվերի արտադրյալը քառակուսի բարձրացնել չէ:

Ակնհայտ է, որ ո՛չ բացասական, ո՛չ դրական թվերի մեջ գոյություն չունի այնպիսի թիվ, որի քառակուսին -4 կամ ցանկացած այլ բացասական թիվ լինի, սակայն եկեք, համառություն ցուցաբերենք, և փորձենք գտնել համապատասխան թիվ ու լուծենք այս խնդիրը:

Սկզբի համար, որքան հնարավոր է՝ առաջադրանքը հեշտացնենք: Ցանկացած թիվ, ասենք՝ 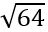 , կարելի է արտադրիչների վերլուծել և գրել  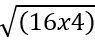տեսքով: Այս արտահայտությունը կարելի է ձևափոխել 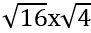տեսքի: Ընդ որում, վերջնական արդյունքը չի փոխվում` 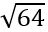=8, 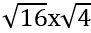=4x2=8։

Ինչքան ուզում ենք նման օրինակներ կարող ենք լուծել, և միշտ այս կանոնը ճիշտ կլինի: Այսինքն, եթե թիվը արտադրիչների բաժանենք, ապա այդ թվի քառակուսի արմատը հավասար կլինի արտադրիչների քառակուսի արմատների արտադրյալին: Այս պնդումը ճիշտ է նաև իռացիոնալ թվերի համար: Օրինակ, 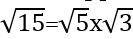: Կարելի է հատուկ աղյուսակներում գտնել, որ  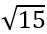հավասար է 3,872983:

Իր հերթին, 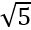=2,236068, 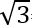=1,732051 (իհարկե, սրանք մոտավոր արժեքներ են): 2,236068х1,732051 արտադրյալը կլինի 3,872983, այսինքն՝ ապացուցեցինք, որ 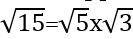: Հիանալի է, կարող ենք այսպիսի սխեմա առաջարկել: Ցանկացած բացասական թիվ հավասար է համապատասխան դրական թվի և -1-ի արտադրյալին: Այլ կերպ ասած՝ -64=64х(-1); -276=276х(-1); -1,98=1,98х(-1) և այլն:

Ցանկացած թվի քառակուսի արմատ, օրինակ -172-ի, կարելի է արտադրիչների բաժանել 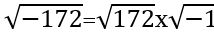: Հետևաբար, եթե գտնենք-1-ի քառակուսի արմատը, կարող ենք ցանկացած բացասական թվի քառակուսի արմատը գտնել: Սակայն այստեղ նորից բախվում ենք անլուծելի թվացող խնդրի. 1x1=1; (-1)х(-1)=1։

Գոյություն չունի այնպիսի թիվ, որը ինքն իր հետ բազմապատկելիս -1 ստացվի: Հետևաբար, միակ բանը, որը կարող ենք անել, այդպիսի թիվ հորինելն է: Կարող ենք պայմանավորվել, որ # սիմվոլը նշանակում է, որ #х# բացասական թվի է հավասար: Այդ ժամանակ #1х#1=-1: Այս արտահայտությունը ճշմարիտ է ըստ սահմանման, իսկ եթե այն ոչ մի մաթեմատիկական դրույթի չի հակասում, այն չօգտագործելու ոչ մի հիմնավորում չկա:

Հասկանալի է, որ այդպիսի թիվն իրական չէ, երևակայական է: Հեշտությամբ կարող ենք պատկերացնել, ինչ է +1$ և -1$-ը: +1$-ը 1$ եկամուտն է, իսկ -1$-ը՝ 1$ ծախսը: Իսկ ինչպե՞ս պատկերացնենք #1$: Մաթեմատիկոսները, որոնք առաջինն օգտագործեցին այս նոր թվերը, դրանք անվանեցին կեղծ: Ի տարբերություն կեղծ թվերի, սովորական դրական և բացասական թվերը, ինչպես ռացիոնալ, այնպես էլ իռացիոնալ, անվանում են իրական:

Մաթեմատիկոսներն այս թվերի համար + նշանի նման նոր նշաններ չհորինեցին, չնայած թվում է, թե դա նպատակահարմար կլիներ: Դրա փոխարեն նրանք 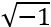-ը նշանակեցին տառային սիմվոլով: Այլ կերպ ասած, ixi=-1, կամ 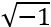=i: Բացի դրանից, -iх-i նույնպես հավասար է i², այսինքն` -1: Պետք է նաև գրենք 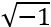=-i: Եվ վերջում, -iхi=-i²=-(-1)=1: Այժմ հեշտությամբ կարող ենք ցանկացած բացասական թվից քառակուսի արմատ հանել:

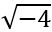-ի արժեքը հավասար է, կամ ±2хi, որն ուղղակի կարելի է գրել ±2i:

Ճիշտ նույն կերպ էլ 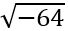արժեքը հավասար է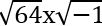, կամ ±8хi, որն ուղղակի կարելի է գրել ±8i, իսկ 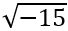արժեքը հավասար է  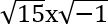, կամ ±3,8729832хi, որն ուղղակի կարելի է գրել ±3,8729832i:

Թվերն ու կոորդինատները ըստ կողմնացույցի

Այնուամենայնիվ հիմա անհանգստանալու հիանալի առիթ ունենք: Ինչ էլ ասեն, ինչպես էլ պայմանավորվեն,  լրիվ անհասկանալի է, թե ինչ են այդ կեղծ թվերը, ինչպես կարելի է դրանք պատկերացնել:

Իրականում այդպիսի թիվը պետք է նշանակի այն, ինչ նրան վերագրել ենք, այն, ինչի մասին նախօրոք պայմանավորվել ենք: Պետք չէ մոռանալ, որ թվերը մարդու  գյուտն են, և նրանց նպատակը Տիեզերքի բացահայտումը հեշտացնելն է, իսկ իր ստեղծածի հետ մարդն իրավունք ունի վարվելու այնպես, ինչպես հարմար է համարում:

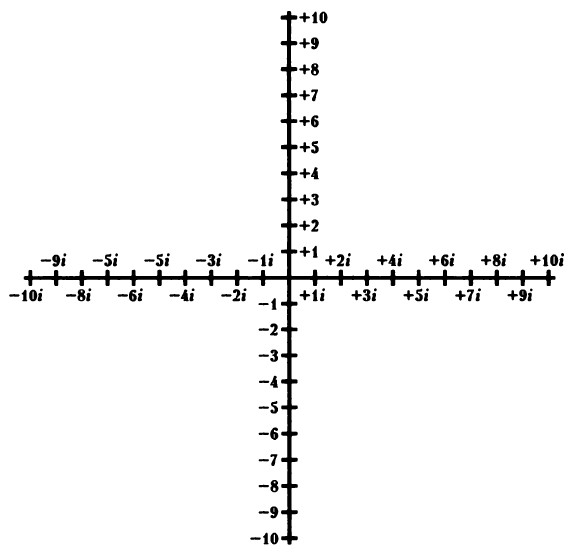Հիշենք, որ հին հույները բացասական թվեր չունեին: Նրանց համար -1-ը նույնքան խորհրդավոր և անհասկանալի էր, որքան մեզ համար  , երբ սկսեցինք կեղծ թվերի ուսումնասիրությունը: Դիմելով բացասական թվերին` օգտագործեցինք թվային առանցքը, որի վրա զրոյից վերև դրական թվերն էին, իսկ ներքև`բացասականները (տե՛ս 2-րդ գլուխը): Այդպիսի սխեման նախորդ անգամ աշխատեց, փորձենք հիմա էլ այն օգտագործել: Զրոյական կետով առաջին թվային առանցքին ուղղահայաց ևս մեկ ուղիղ տանենք: Աջ կողմում հավասար հեռավորությունների վրա նշենք + 1i, +2i, +3i, +4i, +5i, +6i, իսկ ձախում`1i, -2i, -3i, -4i, -5i, -6i... Ստացանք երկու թվային առանցք (տես նկարում)։ 

Այժմ կարող ենք պատկերացնել, թե «i» սիմվոլն ինչ է նշանակում: Արդեն պայմանավորվել էինք, որ +1-ը 1 կմ դեպի հյուսիս, իսկ  -1-ը`դեպի հարավն է: Հիմա էլ պայմանավորվենք, որ +1i-ը 1 կմ դեպի արևելքն է , իսկ -1i-ն՝ 1 կմ դեպի արևմուտք:  (Սա ամենևին չի նշանակում, որ կեղծ թվերն ինչ-որ հեռավորություն են նշանակում: Կեղծ թվերն իրական իմաստ չունեն, սակայն ներկայացված սխեման կոնկրետ օրինակների վրա կօգնի վերացական հասկացություններից և հարաբերություններից ավելի լավ գլուխ հանել:)

Օրինակ, «+» և «-» նշանների փոխարեն կարող ենք, ինչպես կողմնացույցում,  աշխարհի կողմերի տառային նշանակումներն օգտագործել: Պայմանավորվենք, որ դրական իրական թվերը N-թվերն են, բացասական իրական թվերը S-թվերն են, դրական կեղծ թվերը` W-թվերը, իսկ բացասական կեղծ թվերը` Е-թվերը:

Մեր սխեմայում ընդհանրապես պետք չէ «կեղծ թիվ» տարօրինակ տերմինն օգտագործել, քանի որ մեզ մոտ աշխարհի բոլոր կողմերն էլ իրական են: Սակայն այդ տերմինը պատմական խորը արմատներ ունի, և այժմ, երևի անունը փոխելու համար ուշ է:

Այժմ, «կողմնացույցային թվերն» օգտագործելով, կարող ենք ստեղծել մեր սեփական ինքնաբավ հաշվարկման համակարգը (այդպիսի արդյունավետ համակարգի ստեղծումը շատ մաթեմատիկոսների նպատակն է): Բազմապատկման աղյուսակը մեր համակարգում այսպիսի տեսք կունենա.

Չնայած մեր աղյուսակը բավական տարօրինակ տեսք ունի, բայց այն պարզ երկրաչափական մեկնաբանություն ունի, որը ներկայացված է ներքևի նկարներում:

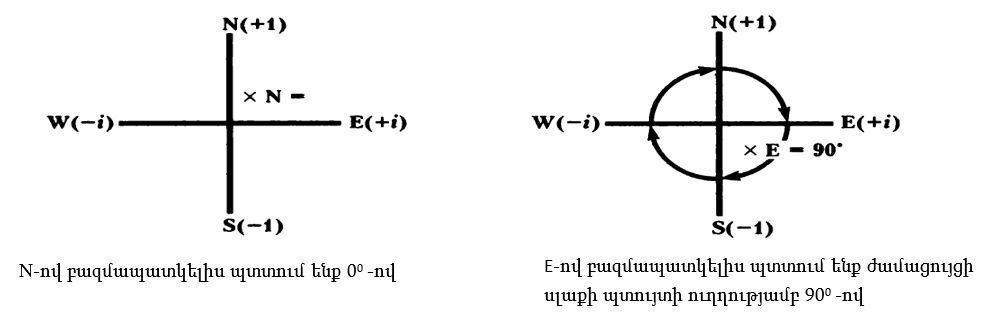
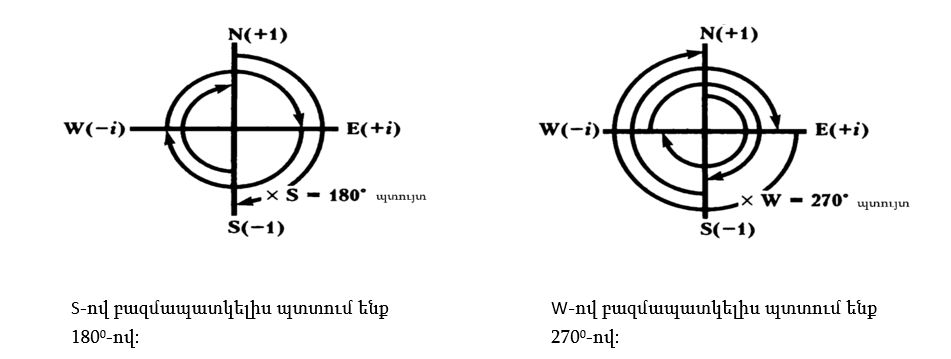
N = դրական իրական թիվ, օրինակ +1:
Е = դրական կեղծ թիվ, օրինակ i:
S = բացասական իրական թիվ, օրինակ -1:
W = բացասական կեղծ թիվ, օրինակ - i:

Բնավ չեմ պնդում, որ միայն մեր համակարգն է ճիշտ, կարող են գոյություն ունենալ նաև այլ համակարգեր՝ նույն չափ ճիշտ և տեսանելի: Ուղղակի առաջարկված համակարգը հարմար է և օգտագործվում է:

Նոր կետեր կողմնացույցի վրա

Եթե խոսեցինք հյուսիսի, հարավի, արևելքի և արևմուտքի մասին, ապա պետք է հիշել նաև այնպիսի ուղղությունների մասին, ինչպիսիք են հյուսիս-արևմուտք, հարավ-արևելք և այլն: Իրական և կեղծ թվերի արտադրյալի արդյունքը համընկնում է արևելք-արևմուտք առանցքի հետ: Իսկ ինչպե՞ս կլինի գումարման դեպքում, օրինակ, ինչի՞ է հավասար 1+i գումարը: Գիտնական-մաթեմատիկոսները հարկ չեն համարել այս արտահայտության համար հատուկ սիմվոլ առաջարկել, դրա համար էլ այն թողնում են 1+i տեսքով, բայց կոորդինատների մեր համակարգում այն կարելի է ակնառու կերպով ներկայացնել:

Այժմ նորից երկու առանցք կառուցենք, բայց յուրաքանչյուր բաժանման արժեքը նշելու փոխարեն այս անգամ յուրաքանչյուր բաժանումով նոր գիծ կառուցենք:

Ենթադրենք, ուղղաձիգ, այսինքն իրական թվերի առանցքի յուրաքանչյուր բաժանումով կառուցել ենք հորզոնական գիծ: +1 բաժանումով ուղիղ ենք գծում, և այդ ուղղի ամբողջ երկարությամբ իրական թվի արժեքը հավասար է +1: Հաջորդ հորիզոնական ուղիղը +2-ով ենք գծում, և այդ ուղղի ամբողջ երկարությամբ իրական թվի արժեքը հավասար է +2: Հաջորդ հորիզոնական ուղիղը գծում ենք  -3-ով, և այդ ուղղի ամբողջ երկարությամբ իրական թվի արժեքը հավասար է -3: Այսպիսի ուղիղներ ինչքան շատ ուզենք հնարավոր է գծել:

Նման գործողություն կարելի է իրականացնել նաև հորիզոնական առանցքով, այսինքն կեղծ թվերի առանցքով:

Հորիզոնական առանցքի, այսինքն՝ կեղծ թվերի առանցքի յուրաքանչյուր բաժանումով ուղղաձիգ ուղիղ ենք գծում: Ինչպես նախորդ դեպքում, +1i բաժանումով անցնող գծի ամբողջ երկայնքով, կեղծ թվի արժեքը հավասար է +1i; +2i բաժանումով անցնող գծի ամբողջ երկայնքով, կեղծ թվի արժեքը հավասար է +2i; իսկ -5i բաժանումով անցնող գծի ամբողջ երկայնքով, երևակայական թվի արժեքը հավասար է -5i:

Ստացանք շախմատի տախտակի յուրօրինակ կաղապար, որտեղ կեղծ թվին համապատասխանող յուրաքանչյուր գծի համար գոյություն ունի իրական թվին համապատասխանող գիծ, և հակառակը, ընդ որում այդ գծերը հատվում են:

Կոմպլեքս թվեր

Այժմ կարող ենք գտնել հարցի պատասխանը` ինչի՞ է հավասար 1+i գումարը: 1+i համապատասխան թիվը մեր կաղապարի վրա  +1 և +i գծերի հատման կետն է: Քանի որ երկու առանցքների վրա բաժանումների միջև եղած հեռավորությունները նույն են, 1+i կլինի հյուսիս-արևելք ուղղությամբ թիվ: Նույն ձևով էլ՝ 2+2i, 3+3i, 4+4i և այլն:

1-i-ի նման թիվը կարելի է ներկայացնել ինչպես +1+(-i), և այն մեր կաղապարի վրա +1 և - i ուղիղների հատման կետն է, այսինքն՝ հյուսիս-արևմուտք ուղղությամբ: Նման ձևով -1+i-ը` հարավ-արևելքն է, իսկ  -1-i-ը հարավ-արևմուտքը: Մյուս ուղղությունները կարելի է ներկայացնել այնպիսի թվերով, ինչպես 15+2i, -7-3i և այլն: Ըստ էության, մեր կաղապարի յուրաքանչյուր կետ (որը, ինչպես արդեն գլխի ընկաք, կարելի է անվերջ ընդլայնել) իրենից ներկայացնում է ինչ-որ թիվ, որն իրական և կեղծ թվերի գումար է: Ավելին, կաղապարի վրա կետի դիրքը կարող է համապատասխանել տասնորդական կոտորակ կամ իռացիոնալ թիվ պարունակող արտահայտության, օրինակ  9,54 + 0,015 i, կամ ։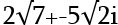

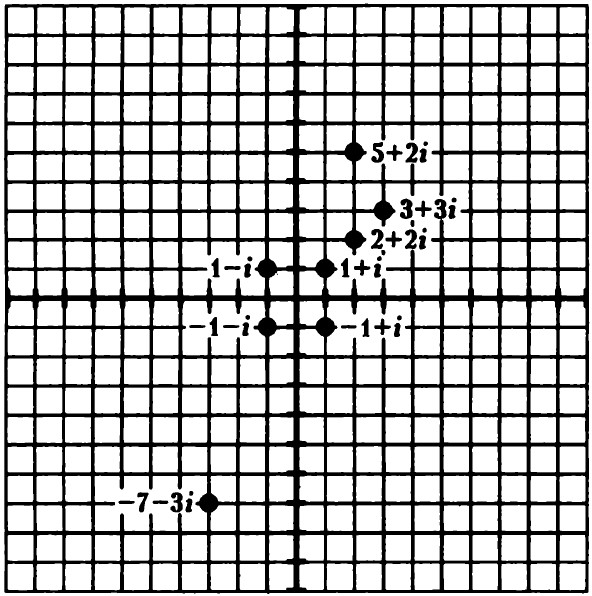
Վերևում ներկայացված թվերը՝ իրական և կեղծ մասերից կազմված, կոչվում են կոմպլեքս: Ցանկացած իրական կամ կեղծ թիվ կարելի է ներկայացնել կոմպլեքս տեսքով, այսինքն՝ 42=42+0i, իսկ 5i=0+5i.

Կոմպլեքս թվերը հետաքրքրություն են ներկայացնում ոչ միայն ճարտարագետների և գիտնականների համար, նրանք հետաքրքիր են նաև առօրյա կյանքում, քանի որ ի տարբերություն սովորական՝ միայն մեծությունը մատնանշող թվերի, նրանք նաև ուղղություն են նշում:

Բերենք օրինակ, որը ցույց կտա կոմպլեքս թվերի դերը: Դիտարկենք այնպիսի ֆիզիկական հասկացություն, ինչպիսիսն ուժն է: Ուժը կարող է լինել հրող ճիգ կամ քաշող ճիգ: Հրող ճիգը դրական մեծություն է, քաշողը`բացասական: Դրանից բացի, ուժը կարող է արժեքը փոխել: Այսպիսով, ուժի արժեքի համար կարող ենք իրական թվեր օգտագործել:

Սակայն, բացի դրանից, ուժը կարող է տարբեր ուղղություններով ուղղված լինել: Ե՛վ հրող ճիգը, և՛ քաշող ճիգը կարող են ուղղված լինել վերև, ներքև, թեքությամբ և այլն:

Ուժի արժեքը կարելի է արտահայտել՝ հաշվի առնելով ուղղությունը, կոմպլեքս թվերի օգնությամբ: Այսպիսով, i թիվը, որը մաթեմատիկայի հետ կապ չունեցող մարդկանց մեծամասնությունը խորհրդավոր, սակայն ընդհանրապես անօգուտ հասկացություն է համարում, պարզ գործնական կիրառություն ունի: Օրինակ, էլեկտրոնիկայի ոլորտում մաթեմատիկական տվյալների ոչ մի մշակում հնարավոր չէ առանց կոմպլեքս թվեր կիրառելու: Փոփոխական հոսանքի մեծությունը փոխվում է ինչպես մեծությամբ, այնպես էլ ուղղությամբ, և նրա նկարագրության համար անհրաժեշտ է կոմպլեքս թվեր օգտագործել:

Կոմպլեքս թվերը կարելի է գումարել և հանել նույն կանոններով, ինչպես սովորական թվերը, ընդ որում, իրական և կեղծ թվերը առանձին են գումարվում և հանվում:

Օրինակ, եթե (+2-4i)-ին ավելացնենք (-5+7i), ապա կստանանք (-3+3i): Եթե (+2-4i)-ից հանենք (-5+7i), ապա կստանանք (7-11i): (Սա կարելի է ցուցադրել մեր կաղապարի վրա, քանի որ սովորական գումարումն ու հանումը կարելի է ցույց տալ հյուսիս-հարավ առանցքի վրա: Կարծում եմ, որ հիմա կարող եք դա ինքնուրույն անել)։

Բայց կոմպլեքս թվերի բազմապատկման դեպքում ավելի մեծ դժվարությունների ենք հանդիպում, քան իրական թվերի դեպքում: 35 և 28 թվերի բազմապատկման ժամանակ, ինչպես արդեն երրորդ գլխում բացատրել եմ, թվերը կարգերի ենք բաժանում, այսինքն՝ 35=30+5, 28=20+8: Այնուհետև թվերը բազմապատկվում են, մեկի յուրաքանչյուր գումարելին մյուսի յուրաքանչյուր գումարելու հետ, և բազմապատկման արդյունքները գումարվում են:

Նույն կերպ էլ կոմպլեքս թվերով են բազմապատկման գործողություն կատարվում:

Որպեսզի բազմապատկենք (3+5i)-ը (6+i)-ով, պետք է այսպիսի սխեմա կազմենք.

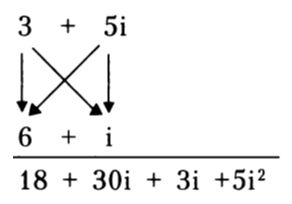
Սլաքներով ցույց է տրված, թե ինչպես են բազմապատկվում կոմպլեքս թվերի բաղադրիչները: Սխեմայի համապատասխան՝ 3х6=18, 3хi=3i, 5iх6=30i, և 5iхi=5i²=-5, քանի որ i ² հավասար է -1:

Միջանկյալ արդյունքներից երկուսը իրական թվեր են, և դրանք կարելի է գումարել, այսինքն՝ 18-5=13: Մյուս երկու բաղադրիչը կեղծ թիվ է, դրանք նույնպես կարելի է գումարել  30i+3i=33i: Այսպիսով, արտադրյալի արժեքը 13+33i կոմպլեքս թիվն է:

Մյուս թվաբանական գործողությունները նույնպես կարելի է նման սխեմայի օգնությամբ ցուցադրել: Այսպիսիով, տեսնում ենք, որ կոմպլեքս թվերով կարելի է աշխատել նույն կանոններով, ինչ սովորական թվերով, ուրեմն նշանակում է, որ կոմպլեքս թվերն էլ խորհրդավոր և անհասկանալի չեն:

Խորանում ենք մինչև արմատները: Ավելի ենք խորանում

Կոմպլեքս թվերի բնագավառը հնարավորություն է տալիս 2-ից մեծ աստիճանացույցով արմատ հանելու մի քանի բարդ դեպքեր ուսումնասիրելու: Արդեն գիտենք, որ 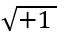հավասար է +1 կամ -1,  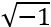հավասար է +i կամ –i:

Իսկ ի՞նչ է հավասար 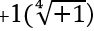-ից չորրորդ աստիճանի արմատը: Ակնհայտ է, որ

(+1)х(+1)х(+1)x(+1)=+1, այսինքն՝ +1-ը չորրորդ աստիճանի արմատ +1-ի արմատներից մեկն է: Ճիշտ նույն ձևով՝ (-1)х(-1)х(-1)х(-1)=+1, այսինքն -1-ը նույնպես +1-ի չորրորդ աստիճանի արմատներից մեկն է: Սակայն դեռ բոլոր տարբերակները չենք քննարկել: Ի՞նչ կասեք  (+i)х(+i)х(+i)х(+i) արտահայտության մասին: (-i)х(-i) արտադրյալի արդյունքը -1-ն է: Հետևաբար, (-i)х(-i)х(-i)х(-i)=(-1)х(-1)=+1: Նշանակում է, որ +i-ը չորրորդ աստիճանի արմատ +1-ի երրորդ արմատն է: Նույն կերպ էլ կարող ենք ցույց տալ, որ  -i-ը չորրորդ աստիճանի արմատ +1-ի չորրորդ արմատն է:

Հետևաբար մեր խնդիրը ունի հետևյալ պատասխանը 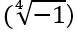=+1, -1, +i, -i : Նույնությամբ կարող ենք ցույց տալ նաև, որ  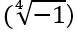հավասար է 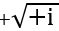, , 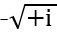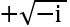կամ 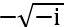, այսինքն՝ այս խնդիրն ունի չորս համարժեք լուծում:

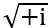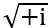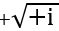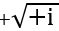Իսկ ի՞նչ է ։ Պատասխանը պարզ է՝ –ն այնպիսի թիվ է, որը ինքն իր հետ բազմապատկելով տալիս է i: Այդ պատճառով x=+i:

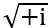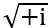Հետևաբար, ()x(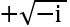-())x()x(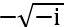)=(+i)x(+i)=-1:

Հետևաբար, (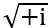)-ը չորրորդ աստիճանի արմատ (-1)-ի արմատներից մեկն է, մյուս արմատներն են` 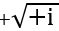, , 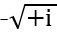 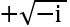և :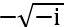

Նույնությամբ էլ կարելի է ցույց տալ, որ ցանկացած թիվ չորրորդ աստիճանի չորս արմատ ունի:

Ցույց տվեցինք, որ ցանկացած թիվ ունի երկու քառակուսի արմատ և չորս չորրորդ աստիճանի արմատ: Կարելի է ենթադրել, որ յուրաքանչյուր թիվ երեք հատ երրորդ աստիճանի արմատ ունի, հինգ հատ հինգերորդ աստիճանի արմատ, վեց հատ վեցերորդ աստիճանի արմատ, քառասունհինգ հատ քառասունհինգերորդ աստիճանի արմատ և այլն: Այս պնդումը բացարձակ ճշմարիտ է, սակայն այն ապացուցելու համար, անհրաժեշտ է բարդ մաթեմատիկական ապարատ, որին չենք տիրապետում, այդ պատճառով էլ առայժմ ուղղակի ընդունենք սա:

Ճիշտ է, այս պնդումը կարող ենք ստուգել երրորդ աստիճանի արմատների համար: Օրինակ, ի՞նչ է հավասար  1-ի խորանարդ արմատը կամ 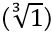: Առաջինը, (+1)х(+1)х(+1)=+1, այսինքն՝ +1-ը  խորանարդ արմատ 1-ի արմատներից մեկն է:

Իսկ ինչի՞ են հավասար մյուս երկուսը: Դիտարկենք բացասական թվերը:

(-1)x(-1)х(-1)=(+1)х(-1)=-1

Այսպիսով, -1-ը 1-ի խորանարդ արմատը չէ: Ավելին, կարելի է ցույց տալ, որ ոչ մի իրական թիվ, ինչպես նաև ոչ մի կեղծ թիվ (լինի -i կամ +i), երրորդ աստիճան բարձրացրած, չի տա +1 արդյունք:

Նշանակո՞ւմ է, որ ընդամենը մեկ արմատ կա, իսկ մյուս երկուսը, ուղղակի չկան: Այդ երկու արմատը գոյություն ունեն, սակայն կոմպլեքս թվերի բնագավառում: Ուղղակի նրանց արժեքը կբերեմ, իսկ դուք կարող եք ստուգել՝ այդ թվերը խորանարդ բարձրացրած ինչի են հավասար: 

Խորանարդ արմատ +1-ի մյուս երկու արմատներն են 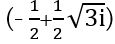 և :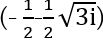

Եկեք այս պնդումը ստուգենք: Եթե 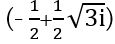-ը +1-ի խորանարդ արմատներից է,

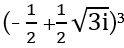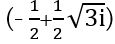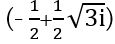կնշանակի, որ   կամ xx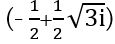

հավասար է 1: Բազմապատկումը կարելի է կատարել վերևում նկարագրված մեթոդով:

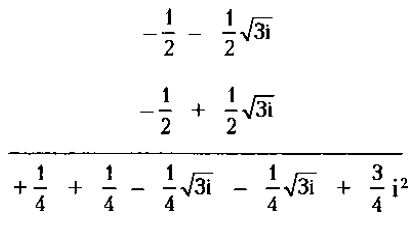
Երկու միջանկյալ կեղծ արդյունքները կարելի է գումարել,

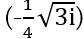   և 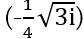 թվերի գումարը հավասար է 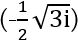: Ինչ վերաբերում է 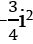, դա հավասար է -3/4 իրական թվին:

Այժմ գումարենք այս արտահայտության երկու իրական բաղադրիչները` 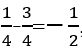, այսպիսով, արտադրյալի արդյունքն է՝ :

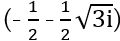Այս արդյունքը պետք է նորից 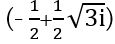-ով բազմապատկել:

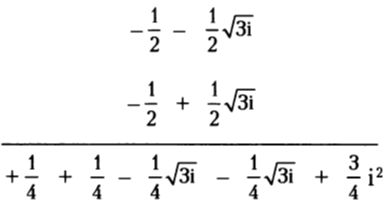
Այս արտահայտությունը երկու կեղծ բաղադրիչների` 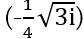  և 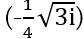 գումարը 0 է, այնպես որ նրանց կարելի է անտեսել: 3/4–ին ավելացնենք մնացած միջանկյալ արդյունքը  և կստանանք 1: Այսպիսով,  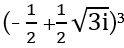հավասար է 1:

Նույն ձևով կարելի է 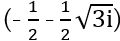 թիվը խորանարդ բարձրացնել:

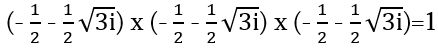
Նույն կերպ էլ կարելի է ցույց տալ, որ -1 թիվը երեք հատ երրորդ աստիճանի արմատ  ունի, որոնցից երկուսը կոմպլեքս են, երեք խորանարդ արմատ ունի  i ու –i թվերից յուրաքանչյուրը:

Եվ ոչ միայն i

Մեր «շախմատի» կաղապարի վրա կարելի է նաև երրորդ գիծ կամ էլ առանցք ավելացնել, այնպես որ բացի հյուսիս, հարավ, արևելք և արևմուտք ուղղություններից  «ներս» և «դուրս» ուղղություններ հայտնվեն: Այսպիսով, «շախմատային տախտակը» հարթ պատկերից փոխակերպվում է ծավալայինի: Այժմ, ինչպես ժամանակին հարթության վրա ցանց ստացանք, կարող ենք խորանադիկներից խճանկար հավաքել:

Երրորդ առանցքը կազմված է հիպերկեղծ թվերից, որոնք j տառով են նշանակում: Հիպերկեղծ առանցքի վրա նույնպես բացասական և դրական միջակայքեր կան, որտեղ համապատասխանաբար, դասավորված են դրականները (+1j, +2j,+3j,+4j,+5j,+6j և այլն) և բացասականները (-1j, -2j,-3j,-4j,-5j,-6j և այլն)

Այժմ թվերը տարածության մեջ գտնվում են հյուսիս-հարավ, արևելք-արևմուտք,  «ներս» և «դուրս» հարթությունների հատման կետերի վրա: Այդ հարթությունների հատման ժամանակ խորանարդներ են  առաջանում, նույն սկզբունքով, ինչպես մեր «շախմատային կաղապարի» քառակուսիների առաջացման ժամանակ: Այդպիսի տարածության յուրաքանչյուր կետն իր սեփական կոորդինատներն ունի, որոնք  հիպերկոմպլեքս թվեր են:

Հեշտ է տարածության մեջ երեք առանցք պատկերացնելը, քանի որ դրանք սովորական երեք չափումներ են՝ երկարություն, լայնություն և բարձրություն: Սակայն մաթեմատիկոսներն աշխատում են մեծ քանակի չափումների հետ: Երբեմն նրանք աշխատում են նույնիսկ այնպիսի համակարգերում, որտեղ առանցքների իրական քանակն անորոշ է: Այդ ժամանակ ասում են «n-չափանի տարածություն», որտեղ n–ը ցանկացած թիվ է:

Շարունակությունը

Թարգմանություն ռուսերենից