Թվեր: Թվաբանությունից մինչև բարձրագույն մաթեմատիկա

Սկիզբը 
Նախորդ հատվածը

Գլուխ 10
Անվերջություն

Յուրաքանչյուրը, որ սկսում է թվերի մասին մտածել, անխուսափելիորեն հանգում է եզրակացության, որ գոյություն ունեն հսկայական քանակի թվեր, և ընդհանրապես անհասկանալի է, ինչպես կարելի է դա արտահայտել: Օգնության է գալիս պոեզիան: Կարող ենք ասել, որ թվերն այնքան շատ են, որքան անապատի ավազահատիկները, կամ օվկիանոսի ջրի կաթիլները կամ երկնքում առկայծող աստղերը: Բայց մաթեմատիկոսի համար այդպիսի համեմատություններն անօգուտ են: Մաթեմատիկոսի տեսանկյունից, ցանկացած թվին կարող ենք մեկ ավելացնել և հաջորդ թիվն ստանալ, այնուհետև ստացված թվին մեկ ավելացնել և այդպես շարունակ: Քանի որ մաթեմատիկայում գումարման գործողության համար ոչ մի սահմանափակում չկա, կարելի է ցանկացած երկու թիվ գումարել և, հետևաբար, այդ գործընթացն անվերջ է: Այսպիսով, կարող ենք կամայական մեծ թիվ վերցնել, ավելացնել մեկ և ավելի մեծը ստանալ: Կարող ենք պատկերացնել թիվ, որի երկարությունը հավասար է ամենահեռավոր աստղի հեռավորությանը, և նրան էլ կարելի է մեկ ավելացնել ու ստանալ էլ ավելի մեծ թիվ:

Ամբողջ թվերի 1, 2, 3..., հաջորդական գրառումն իրենից անվերջություն է ներկայացնում, այսինքն՝ վերջ չունեցող ինչ-որ բան: Երբ գրում ենք 1, 2, 3.., նշանակում է «1, 2, 3 և մինչև անվերջություն»:

Ճիշտ այդպիսի եղանակով էլ կարող ենք բացասական թվերի շարքը գրել՝ -1, -2, -3..., որն էլ նշանակում է «-1, -2, -3 և մինչև անվերջություն», կամ դրական և բացասական կեղծ թվերի՝ + 1i, +2i, +3i ... կամ -1i, -2i, -3i...

Հիմա եկեք ուրիշ թվային շարք գրենք՝ զույգ թվերի շարքը՝ 2, 4, 6, 8 և այլն: Քանի՞ զույգ թիվ կա:

Սովորական առողջ բանականության տեսանկյունից կարելի է ասել, որ զույգ թվերը երկու անգամ քիչ են, քան բոլոր ամբողջ թվերն իրար հետ, քանի որ ամբողջ թվերը տրոհվում են զույգերի և կենտերի: Ասենք, առաջին տասը թվերից հինգը զույգ են, իսկ հինգը՝ կենտ:

Բայց դա այդպես չէ: Ախր ամբողջ թվերի քանակն անվերջ է, և չենք կարող խոսել «անվերջության կեսի» մասին:

Քննարկենք զույգ թվերի շարքն այլ տեսակյունից: Ինչպիսի զույգ թիվ էլ որ վերցնենք, ինչքան ուզում է մեծ, կարելի է նրան 2 ավելացնել և ստանալ ավելի մեծ զույգ թիվ: Նույնիսկ եթե պատկերացնենք հսկայական զույգ թիվ, որի թվանշանները ձգվում են ամենահեռավոր աստղի մոտ, նրան էլ կարող ենք 2 ավելացնել և ավելի մեծ թիվ ստանալ:

Նույնը կարելի է ասել կենտ թվերի շարքի մասին՝ 1, 3, 5, 7..., և՛ 5-ին բազմապատիկ թվերի շարքի մասին, այսինքն՝ 5, 10, 15, 20, 25..., և՛ միլիոնի բազմապատիկ, այսինքն՝ 1000000, 2000000, 3000000... թվերի շարքի մասին: Բոլոր այդ շարքերն անվերջ են, և այդպիսի շարքեր պատկերացնելով՝ պատկերացում եք կազմում «անվերջություն» հասկացության մասին:

Հաշիվ առանց հաշվելու

Այնուամենայնիվ, իմ բացատրությունը կարող է ձեզ չբավարարել: Ախր, այնքան ակնհայտ է թվում, որ զույգ թվերը պետք է երկու անգամ քիչ լինեն, քան ամբողջ թվերը, նույնիսկ, եթե նրանց թիվն անվերջ է, իսկ միլիոնի բազմապատիկ թվերը, պետք է միլիոն անգամ քիչ լինեն, քան բոլոր ամբողջ թվերը:

Սակայն ոչ միշտ է լինում, որ ակնհայտ թվացողն իրական լինի: Ակնհայտ է թվում, երբ մարդը դեմքով դեպի հյուսիս է կանգնած, մեջքով շրջված է դեպի հարավ: Ո՞վ կառարկի սրան: Բայց եթե նա Հարավային բևեռում է կանգնած, դա իրականությանը չի համապատասխանում: Ե՛վ նրա դեմքը, և՛ մեջքը ուղղված կլինեն հյուսիս:

Եկեք այնուամենայնիվ թվերից գլուխ հանենք: Պարզենք՝ ինչպիսի հարաբերակցություն գոյություն ունի զույգ թվերի և ամբողջ թվերի քանակների միջև: Բայց դա ինչպե՞ս անենք, ախր, ամբողջ թվերն անվերջ են: Այդուհանդերձ, այդպիսի հաշվարկի մեթոդ կա:

Ինչպե՞ս ենք սովորաբար հաշվում առարկաները: Ամբողջ թվերի աճող հաջորդականությունից յուրաքանչյուր առարկայի մի համապատասխան թիվ ենք վերագրում: Առաջին առարկան համար մեկ առարկան է, երկրորդը՝ համար երկուսը, և այլն: Եթե վերջին առարկան համար տասն է, նշանակում է ձեզ մոտ ընդամենը տասը առարկա է:

Իսկ կարելի՞ է առանց թվերի հաշվել: Դա գրեթե նույնն է, ինչ հարցնեն. «Իսկ կարելի՞ է հաշվել առանց հաշվելու»: Որքան էլ տարօրինակ է, բայց հնարավոր է:

Պատկերացնենք, որ մեր շուրջը աղմկոտ երեխաների խումբ է հավաքված, որոնց պետք է սառնաշաքար բաժանենք: Ո՛չ գիտենք՝ քանի երեխա է սառնաշաքար պահանջում, ո՛չ էլ քանի սառնաշաքար ունենք տուփի մեջ: Սակայն տարբերակ չունենք, և սկսում ենք բաժանել՝ յուրաքանչուր մանչուկի մեկ սառնաշաքար: Եթե տուփը դատարկվելու պահին յուրաքանչյուր երեխա սառնաշաքար է ծծում ուրեմն, սառնաշաքարների քանակը հավասար է երեխաների քանակին: Եթե բոլոր փոքրիկներին սառնաշաքար նվիրենք, ու տուփի մեջ էլի սառնաշաքար մնա, ուրեմն, սառնաշաքարների քանակը երեխաների քանակից ավելի է: Եթե, հակառակը, բոլորին սառնաշաքար չհասնի, նշանակում է, որ երեխաներն ավելի շատ են, քան սառնաշաքարները:

Հաշվարկի այսպիսի մեթոդը՝ հաջորդական շարքերը համեմատելը (մեկ սառնաշաքար՝մեկ երեխայի, կամ մեկ զույգ թիվ՝ մեկ ամբողջ թվի դիմաց), կօգնի բացահայտելու, թե հավասար են արդյոք թվերի երկու շարքերը, և եթե նրանք հավասար չեն, ապա որ շարքն է ավելի մեծ:

Ամբողջ թվերի շարք գրենք, իսկ նրանց տակ զույգ թվերի շարք.

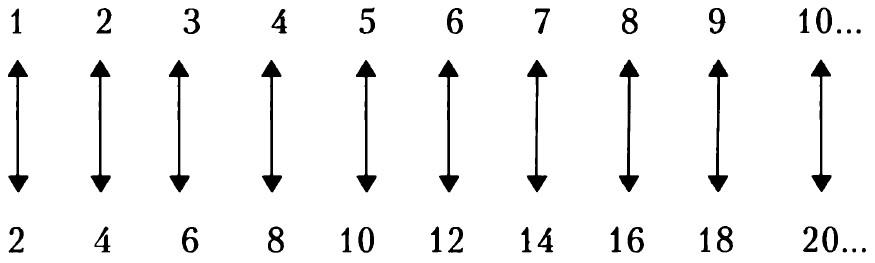
Տեսնում ենք, որ յուրաքանչյուր ամբողջ թվի համար մի զույգ թիվ կա, ընդ որում այն կարելի է ստանալ համապատասխան ամբողջ թիվը 2-ով բազմապատկելով:

Տեսնում ենք, որ ինչքան էլ շատ թվեր գրենք, յուրաքանչյուր ամբողջ թվին համապատասխանում է որոշակի զույգ թիվ, և, հակառակը, յուրաքանչյուր զույգ թվին համապատասխանում է որոշակի ամբողջ թիվ (այսինքն՝ յուրաքանչյուր երեխայի բաժին է հասնում մեկ սառնաշաքար):

Սա ի՞նչ է նշանակում: Կարո՞ղ ենք պնդել, որ զույգ թվերի քանակը հավասար է ամբողջ թվերի քանակին: Այնքան էլ այդպես չէ: Հարցն այն է, որ երբ խոսքը անվերջության մասին է, չենք կարող ասել, որ մեկ անվերջությունը հավասար է մյուս անվերջությանը: Սակայն կարող ենք պնդել, որ ամբողջ թվերի և զույգ թվերի հաջորդականությունների միջև գոյություն ունի մեկը մեկին համապատասխանություն, այսինքն՝ զույգ թվերի հաջորդականությունը փոխմիարժեք է ամբողջ թվերի հաջորդականության հետ: Նշանակում է, որ եթե հարաբերակցենք զույգ թվերի հաջորդականությունը ամբողջ թվերի հաջորդականության հետ, ապա յուրաքանչյուր ամբողջ թվի համար իր զույգ թիվը կգտնվի, և հակառակը:

Նույն ձևով կարող ենք համեմատել ամբողջ թվերի հաջորդականությունը միլիոնին բազմապատիկ թվերի հետ: Յուրաքանչյուր ամբողջ թվի համար կարելի է գրել միլիոնի բազմապատիկ համապատասխան թիվ, որը կստանանք տվյալ ամբողջ թիվը միլիոնով բազմապատկելով: 1-ի համար կլինի 1000000, 6-ի համար՝ 6000000, իսկ 234-ի համար՝ 234000000: Այսինքն՝ կարելի է ասել, որ յուրաքանչյուր ամբողջ թվին համապատասխանում է միլիոնի բազմապատիկ թիվ, կամ որ այս երկու հաջորդականությունները «մեկ-մեկ» համապատասխանության մեջ են կամ էլ փոխմիարժեք են: Թվերի ցանկացած հաջորդականություն, որը ամբողջ թվերի հաջորդականության հետ փոխմիարժեք է, կոչվում է հաշվելի: Ամբողջ թվերի հաջորդականությունը նույնպես հաշվելի է:

Անվերջությունը՝ փոքրում

Երբ խոսքն անվերջության մասին է, մեր երևակայության մեջ հայտնվում է ինչ-որ բան՝ հսկայական և հավերժական, անհասկանալի և, թերևս, անօգտակար:

Սակայն, նույնիսկ եթե փոքր թվերի հետ գործ ունենք, լրիվ անսպասելի մեր տեսադաշտում նորից հայտնվում է «անվերջություն» հասկացությունը: Ենթադրենք, որ պետք է 1-ը բաժանել 1/10-ի: Հիշում ենք հակադարձ մեծությունների կանոնները և գիտենք, որ թիվը բաժանել 1/10-ի, նույն է, ինչ բազմապատկել 10-ով: Այսպիսով, 1:1/10= 10; 1:1/100=100; 1:1/1000=1000: Այսինքն, միևնույն բաժանելիի համար ինչքան փոքր է բաժանարարը, այնքան մեծ է քանորդը:

Իսկապես, եթե մեկը կամ ցանկացած այլ թիվ, բաժանենք հաջորդաբար նվազող, այսինքն՝ ավելի ու ավելի փոքրացող թվերի շարքի վրա, կստանանք շարք թվեր (քանորդներ), որոնք ավելի ու ավելի մեծ են դառնում: Իսկ երբ բաժանարարը անվերջ փոքր մեծություն է դառնում, քանորդն ընդունում է անվերջ մեծ արժեք:

Կարող եք հարցնել՝ ի՞նչ է «անվերջ փոքր մեծությունը»: Իհարկե, ամենափոքր մեծությունը զրոն է: Սակայն փոքր մեծությունը կարող է կոտորակ լինել: Ասենք, 1/10-ը փոքր մեծություն է, 1/100-ը՝ ավելի փոքր, 1/1000-ը՝ էլ ավելի փոքր, իսկ 1/100000-ը՝ էլ ավելի: Գոյություն չունի սահման, մինչև որը կարելի է արժեքները փոքրացնել: Բայց ինչքան էլ հայտարարում զրոների քանակն ավելացնենք, երբեք զրոյին չեք հասնի: Այսպիսով, երբ մեկը կամ մեկ ուրիշ թիվ բաժանում եք անվերջ մեծացող թվերի հաջորդականության, անվերջ փոքրացող թվերի հաջորդականություն կստանաք: Երբ բաժանարարն անվերջ մեծ թիվ է դառնում, քանորդը դառնում է անվերջ փոքր:

Ուշադրություն դարձրեք, որ չենք կարող թիվը զրոյի բաժանել: Այդ գործողությունը մաթեմատիակայում չի դիտարկվում, և պատճառը պարզ է: Ասենք, ի՞նչ քանորդ կստանանք 6-ը 0-ի բաժանելուց: Այլ կերպ ասած, 0-ն ի՞նչ թվով պետք է բազմապատկենք 6 ստանալու համար: Այդպիսի թիվ չկա, ուրեմն 6:0-ն անհնար գործողություն է: Ցանկացած թիվ զրոյով բազմապատկելիս զրո է ստացվում: Նշանակում է, որ ոչ մի թիվ զրոյի չենք կարող բաժանել:
Երկու թվերի միջև եղած միջակայքը, ասենք մեկի և երկուսի միջև, կարելի է ցանկացած քանակի մասերի տրոհել՝ միլիոն, տրիլիոն և այլն, անվերջ: Նույնը կարելի է անել և փոքր միջակայքերով, ասենք ¼-ի և ½-ի միջև, կամ 0,0000001-ի և 0,00000001-ի միջև:

Մաթեմատիկոսները ապացուցել են, որ բոլոր հնարավոր կոտորակները (այսինքն բոլոր ռացիոնալ թվերը) կարելի է դասավորել այնպես, որ ամբողջ թվերի հաջորդականության հետ փոխմիարժեք համապատասխանություն ստանանք:
Յուրաքանչյուր ամբողջ թվի համար համապատասխան կոտորակ գոյություն կունենա, և հակառակը` առանց համապատասխան թվի կոտորակ գոյություն ունենալ չի կարող: Այսպիսով, բոլոր հնարավոր կոտորակների հաջորդականությունը հաշվելի հաջորդականություն է:

Ավելի ու ավելի մոտ

Դիտարկենք կոտորակների անվերջ հաջորդականություն.

Ուշադրություն դարձրեք, որ յուրաքանչյուր հաջորդ կոտորակը նախորդի կեսին է հավասար, քանի որ հայտարարը յուրաքանչյուր անգամ կրկնապատկվում է: (Եթե վերցնենք ցանկացած կոտորակ և բաժանենք 2-ի, օրինակ  , ապա նույն է, որ բազմապատկենք  1/2-ով, այսինքն   , իսկ դա նշանակում է, որ հայտարարը կրկնապատկվում է):

Չնայած կոտորակները միշտ նվազում են, այս հաջորդականությունը ևս անվերջ է, քանի որ այս հաջորդականությունից ցանկացած կոտորակ կարելի է երկուսի բաժանել և ավելի փոքր կոտորակ ստանալ: Կոտորակի հայտարարն անվերջ մեծանում է, սակայն կոտորակը չի հասնի զրոյի, քանի որ դրա համար պետք է հայտարարը հասնի անվերջության, ինչը հնարավոր չէ:

Իսկ այժմ, եկեք պարզենք, ինչի է հավասար այս անվերջ հաջորդականության գումարը: Սովորական առողջ բանականության տեսանկյունից կարող է թվալ, որ այդպիսի հաջորդականության գումարը պետք է անվերջ մեծ արժեք լինի: Սակայն արդեն գիտենք, թե այսպես կոչված «առողջ բանականությունը» որքան խաբուսիկ է լինում:

Սկզբում ½-ին ավելացնենք ¼, կստանանք 3/4, այնուհետև ¾-ին ավելացնենք 1/8, կստանանք 7/8, այնուհետև 7/8-ին ավելացնենք 1/16, կստանանք 15/16, ավելացնենք 1/32, կստանանք 31/32, և այսպես շարունակ:

Ուշադրություն դարձրեք, որ ինչքան հաջորդականությանն ավելի շատ անդամներ ենք գումարում, այնքան հաջորդականության գումարը մոտենում է 1-ի: Երբ գումարում ենք շարքի առաջին երկու անդամները, մեկից 1/4 է պակասում, գումարում ենք հաջորդ անդամը, մեկին մնում է 1/8, և այդպես շարունակ կարելի է հասնել մինչև մեկ միլիոներորդին կամ մեկ տրիլիոներորդին, բայց մեկին այդպես էլ չենք հասնի:

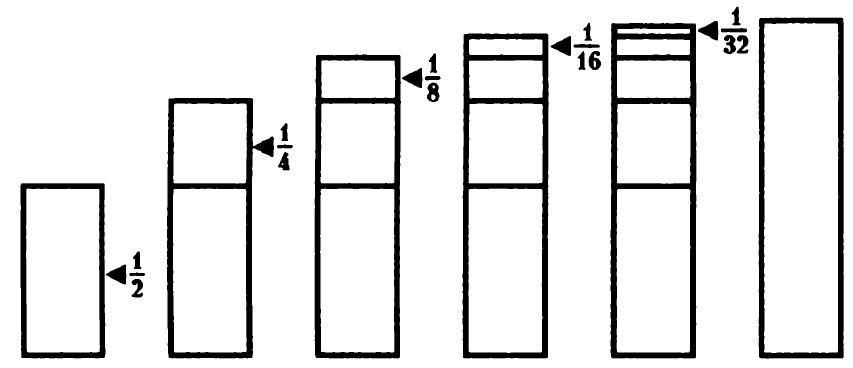
Մաթեմատիկոսներն այս դրույթը ձևակեպում են. «1/2, ¼, 1/8,... կոտորակների անվերջ հաջորդականության գումարը մոտենում է մեկի, որն էլ տվյալ հաջորդականության գումարի սահմանն է»:

Սա զուգամետ հաջոդականության օրինակ է, այսինքն՝ անվերջ անդամներից կազմված հաջորդականության, որոնց գումարը որպես սահման մոտենում է ինչ-որ վերջնական թվի:

Դեռևս Հին Հունաստանում են մաթեմատիկոսները հայտնաբերել զուգամետ հաջորդականություն, սակայն նրանք այնքան զարմացել էին, որ հաջորդականության անդամների քանակն անվերջ է, որ չէին կարող պատկերացնել, թե այդպիսի հաջորդականության գումարը կարող է անվերջ մեծություն չլինել:

Հույն մաթեմատիկոս և փիլիսոփա Զենոնը մի շարք խնդիրներ ձևակերպեց, այսպես կոչված՝ պարադոքսներ, որոնք, թվում էր, թե հերքում են լիովին ակնհայտ դրույթները: Նրա պարադոքսներից մեկն ապացույց էր, որ շարժում սկզբունքորեն հնարավոր չէ: Այս պարադոքսները հարուրամյակներ շարունակ անլուծելի էին համարվում, մինչև զուգամետ անվերջ հաջորդականության մասին ճշմարտությունը բացահայտվեց:

Զենոնի ամենահայտնի պարադոքսը կոչվում է «Աքիլեսը և կրիան»: Հին հունական հերոս Աքիլեսը հայտնի էր որպես հիանալի վազորդ, իսկ կրիան հայտնի է նրանով, որ շատ դանդաղ է շարժվում: Այնուամենայնիվ Զենոնը ցույց տվեց, որ Աքիլեսը երբեք չի կարող վազքի մրցույթում կրիային հաղթել, եթե ի սկզբնե կրիան առավելություն ունենա:

Ենթադրենք, որ Աքիլեսը կրիայից տասն անգամ ավելի արագ է վազում, սակայն մրցույթի սկզբում կրիան 100 յարդ առավելությունը ունի: Մի քանի ցատկով Աքիլեսը 100 յարդը կանցնի, սակայն այդ ժամանակահատվածում կրիան, որը Աքիլեսից տասն անգամ դանդաղ է շարժվում (ինչը կրիայի համար այնքան էլ վատ չէ), 10 յարդ կանցնի: Աքիլեսը այդ 10 յարդն էլ կվազի, սակայն կրիան նրանից 1 յարդ հեռու կլինի: Երբ Աքիլեսը վազի մեկ յարդը, կրիան 1/10 յարդ կանցնի, և այդպես մինչև անվերջություն:

Տեսնում եք, ինչ է կատարվում: Աքիլեսը շարունակում է շարժումը, բայց կրիան էլ է շարժվում, և Աքիլեսը չի կարողանում նրան հասնել: Ավելին, կրկնելով այս դատողությունն Աքիլեսի և կրիայի միջև նախնական այլ տարբերությամբ, կարող ենք ասել, որ ինչքան էլ կրիայի նախնական առավելությունը փոքր լինի, լինի դա մեկ ֆուտ կամ մեկ դյույմ, ոչինչ չի փոխվի: Աքիլեսը երբեք չի կարող ոչ մի առավելության հասնել, իսկ սա իր հերթին, նշանակում է ընդհանրապես շարժման անհնարինություն:

Իհարկե, շատ լավ գիտեք, որ Աքիլեսը կարող է կրիային հաղթել, և շարժումը հնարավոր է, հետևաբար, Զենոնի ապացույցն իր մեջ հակասություն ունի, այսինքն՝ պարադոքս է:

Իսկ այժմ հանգամանալից ուսումնասիրենք Զենոնի խնդիրը: Նրա դատողություններում ո՞րն է սխալը: Ենթադրենք, Աքիլեսը վազում է վայրկյանում 10 յարդ արագությամբ, իսկ կրիան շարժվում է վայրկյանում 1 յարդ արագությամբ: Աքիլեսն առաջին 100 յարդը կվազի 10 վայրկյանում: Այդքան ժամանակում կրիան կանցնի 10 յարդ: Աքիլեսը 10 յարդն անցնում է մեկ վայրկյանում, իսկ կրիան այդ ժամանակում անցնում է մեկ յարդ: Աքիլեսն այդ յարդը հաղթահարում է 0,1 վայրկյանում, իսկ կրիան նրանից 0,1 յարդ հեռու է:

Այլ կերպ ասած, ժամանակը, որն անհրաժեշտ է Աքիլեսին, որպեսզի կրիային հասնի, նվազող հաջորդականություն է՝ 100, 10, 1, 0,1, 0,01, 0,001, 0,0001, 0,00001...

Որքա՞ն ժամանակ անհրաժեշտ կլինի Աքիլեսին, որպեսզի հաղթահարի կրճատվող տարածության անվերջ հաջորդականությունը: Զենոնը համարում էր, որ եթե հաջորդականության անդամների քանակն անվերջ է, ուրեմն գումարն էլ պետք է անվերջ լինի: Նա չէր կարող պատկերացնել, որ անվերջ քանակի թվերի հաջորդականությունը կարող է զուգամետ լինել և վերջական գումար ունենալ:

Օրինակ, եթե Զենոնի հաջորդականության առաջին երկու անդամները գումարենք, 11 կստանանք, առաջին երեք անդամների գումարը հավասար է 11,1, առաջին չորսինը` 11,11, առաջին հինգինը` 11,111, առաջին վեցինը` 11,1111: Իսկ եթե պատկերացնենք անվերջ շարքի գումարը 11,11111111111111111... կստանանք: Եվ այսպես մինչև անվերջություն:

Սա  թվի տասնորդական համարժեքն է: Եթե  տասնորդական կոտորակի տեսքով ներկայացնենք, հենց 11,11111111111111111... կստանանք:

Այսպիսով, Զենոնի խնդրում հաջորդականության գումարը  վայրկյան է: Սա այն ժամանակն է, որն անհրաժեշտ է Աքիլեսին, որպեսզի հաղթահարի նվազող հեռավորությունները, որոնք կրիան անցել է: Նշանակում է, առաջին՝ որ Աքիլեսը վերջիվերջո կհասնի կրիային, երկրորդ՝ որ շարժումը հնարավոր է, և վերջապես երրորդ՝ որ կարող ենք վերջապես հանգստանալ:

Հաջորդականությունները կարող են սահմանի ձգտել, որը անվերջ տասնորդական կոտորակ է, ընդ որում չկրկնվող թվանշաններով: Այսպիսի հաջորդականություններ կարելի է կազմել իռացինոնալ թվերը ցույց տալու համար: Այսպիսի հաջորդականությանը նոր անդամներ ավելացնելով, ավելի ենք մոտենում իռացիոնալ թվի արժեքին, չնայած երբեք չենք կարող նրան հասնել: Այսպիսի զուգամետ հաջորդականություններն օգտագործում են իռացիոնալ թվերը, օրինակ լոգարիթմները, սահմանելու համար:

Ավելին, քան անվերջը

Բոլո՞ր անվերջություններն են հավասարապես անվերջ: Կարելի՞ է պատկերացնել անվերջ հաջորդականություն, որը ամբողջ թվերի հաշվելի անվերջ հաջորդականություն չէ:

Այո, ընդհանրապես, հնարավոր է: Պատկերացրեք ուղիղ՝ հավասար միջակայքերով, որոնք նշանակված են թվերով. մեր գրքում նյութի մատուցման ընթացքում այդպիսի ուղղի հետ մի քանի անգամ առնչվել ենք: Իսկ հիմա պատկերացրեք, որ թվերի միջև բոլոր միջակայքերը բաժանված են ամենահնարավոր կոտորակների: Այսինքն՝ ամբողջ թվերի միջև միջակայքերը կիպ լցված են երրորդական մասերով, յոթերորդական մասերով, հազարերորդականներով, միլիոներորդականներով և այդպես շարունակ: Այնուամենայնիվ, ուղղի վրա կմնան կետեր, որոնց չի համապատասխանի ոչ մի կոտորակ, նույնիսկ այն դեպքում, երբ կոտորակներն անվերջ քանակով լինեն: Հիշեք իռացիոնալ թվերը:

Օրինակ, քառակուսի արմատ 2-ը կոտորակների ուղղի վրա կետ չունի, որովհետև անհնար է նրան կոտորակի տեսքով պատկերելը: Այնուամենայնիվ, ուղղի վրա այն գոյություն ունի: Պատկերացրեք, քառակուսի՝ մեկ ամբողջ թվից մինչև մյուսը կողմով (ինչպես նկարում է):

Այդ քառակուսու անկյունագիծը հավասար է քառակուսի արմատ 2-ից, և եթե այդ անկյունագծի երկարությանը հավասար հատվածը դնենք ուղղի զրոյական կետից, ապա այն կավարտվի քառակուսի արմատ 2-ի մոտ, որին ոչ մի կոտորակ չի համապատասխանում: Այդ կետում ոչ մի կոտորակ ուղղակի չի կարող գտնվել: Ուղղի վրա կարելի է նշել նաև ցանկացած ուրիշ իռացիոնալ թիվ, և նորից այդ կետին ոչ մի կոտորակ չի համապատասխանի:

Ողջ ասվածից ի՞նչ եզրակացություն կարելի է անել: Եթե ուղղի վրա բոլոր ռացիոնալ թվերը կետերով են նշված, այնուամենայնիվ իռացիոնալ թվերին համապատասխանող անթիվ քանակի կետեր կմնան: Ավելին, ռացիոնալ թվերին համապատասխանող երկու կետեր երբեք իրար կողքի չեն լինի:

Մաթեմատիկոսներն ապացուցել են, որ նրանց միջև, համենայնդեպս, միշտ իռացիոնալ թվի համապատասխանող կետ կլինի: Եվ հակառակը, երկու իռացիոնալ թվերի միջև միշտ գոնե մեկ ռացիոնալ թիվ կլինի: Եթե ուղղի վրա նշված լինեն բոլոր ռացիոնալ և իռացիոնալ թվերը, կնշանակի, որ բոլոր կետերն օգտագործված են: Իրական թվերի հաջորդականությունը, որտեղ ներառված են ինչպես ռացիոնալ, այնպես էլ իռացիոնալ թվերը, «կոնտինիուում» է ձևավորում:

Իսկ իրական թվե՞րը: Իրական թվերի հաջորդականությունը ամբողջ թվերի հաջորդականության հետ հաշվելի՞ է, ինչպես բոլոր ռացիոնալ թվերի հաջորդականությունը: Ոչ, հաշվելի չէ: Ապացուցված է, որ ինչքան էլ փորձենք իրական թվերը դասավորել այնպես, որ մեկ իրական թվին համապատասխանի մեկ ամբողջ թիվ, միևնույն է, անվերջ քանակությամբ ազատ իրական թվեր կմնան:

Իրական թվերի անվերջությունը նշանակում են С (լատիներեն «continuum»): С անվերջությունը ավելի ընդարձակ է, քան հաշվելի անվերջությունը, քանի որ ամբողջ թվերի անվերջ հաջորդականությունը բավարար չէ, որպեսզի իրական թվերի անվերջ հաջորդականությունը հաշվենք:

Կարելի է ստուգել, արդյոք անվերջ հաջորդականության ուրիշ տեսակներ իրական թվերի հաջորդականության հանդեպ հաշվելի են: Օրինակ, բոլոր կոմպլեքս թվերի հաջորդականությունը (այսինքն՝ ոչ միայն ուղղի, այլև հարթության բոլոր կետերը) բոլոր իրական թվերի հաջորդականության հանդեպ հաշվելի է: Հենց այդպես էլ հիպերկոմպլեքս թվերի անվերջ հաջորդականությունը (այսինքն Տիեզերքի, որը նույնպես անվերջ ենք համարում, տարածության բոլոր կետերը,) բոլոր իրական թվերի հաջորդականության հանդեպ համարվում է հաշվելի:

Անվերջ անվերջություններ

1896 թվին մաթեմատիկոս Ջորջ Կանտորը առաջ քաշեց «տրանսֆինիտ թվերի» տեսությունը, որի համաձայն գոյություն ունեն անվերջ քանակի տարբեր տեսակի անվերջություններ: Այդ անվերջությունները նա նշանակեց հին հրեական այբուբենի «ալեֆ» տառով: Յուրաքանչյուր այդպիսի անվերջություն նշանակում էին «ալեֆ» տառի աջ ներքևի ինդեքսի օգնությամբ:

Առաջին անվերջությունը կոչվում է «ալեֆ-զրո» և համապատասխանում է ամբողջ թվերի անվերջ հաջորդականությանը: Դա նշանակում է, որ անվերջությունը, որի նկարագրությամբ սկսեցի այս գլուխը, կարող է գոյություն ունեցող անվերջություններից ամենափոքրը լինել: Այլ կերպ ասած, մինչ այժմ հայտնաբերված չէ այնպիսի անվերջ հաջորդականություն, որը ամբողջ թվերի հաջորդականության նկատմամբ հաշվելի չլինի հենց այն պատճառով, որ ավելորդ ամբողջ թվեր կմնան:

Համարվում է, որ հերթականությամբ հաջորդ հաջորդականությունը` «ալեֆ-մեկ», С կամ կոնտինիում անվերջությունն է, սակայն այս դրույթը դեռևս ապացուցված չէ: Ոչ մեկին չի հաջողվել «ալեֆ-զրո»-ի և С-ի միջև հայտնաբերել ինչ-որ բանի անվերջ հաջորդականություն, բայց ոչ ոք նաև չի ապացուցել, որ այդպիսի անվերջության գոյությունն անհնար է:

Բազմազան կորերի քանակի անվերջությունը, որը կարելի է հարթության վրա նկարել, կարող է լինել «ալեֆ-երկու» անվերջությունը:

Ինչ վերաբերում է հերթականությամբ հաջորդ անվերջություններին, նրանց համար դեռևս համապատասխանություն գտնված չէ: Այնուամենայնիվ արդեն գոյություն ունի անվերջությունների անվերջ բազմազանության կոնցեպցիան, որը սկսվում է ամենափոքր հնարավոր անվերջություններից՝ սովորական ամբողջ թվերի անվերջ հաջորդականությունից:

Այսպիսով, զարգացման արշալույսին 1-ն ու 2-ը տարբերել սովորած մարդը փորձերի և սխալների ճանապարհով շարժվել է դեպի գիտելիքների բարձունքը և մեր օրերում կարող է խիզախորեն աշխատել այնպիսի հասկացություններով, ինչպիսիք են անվերջությունների բազմազանությունը:

Մարդկության ձեռքբերումներին նվիրված ցանկացած գրքի վերջում «վերջ» բառը չպետք է գրել, քանի որ վերջ գոյություն չունի, իսկ ճանաչման գործընթացն անվերջ է: Անհրաժեշտ է դնել նշանը:

Թարգմանություն ռուսերենից
Լուսանկարի աղբյուրը